Задание 3
Трем
поставщикам А1,
А2,
А3
поступил
однородный груз в количестве:
 тонн – поставщику А1;
тонн – поставщику А1;
 тонн – поставщику А2;
тонн – поставщику А2;
 тонн – поставщику А3.
Полученный груз требуется перевести
пяти потребителям:
тонн – поставщику А3.
Полученный груз требуется перевести
пяти потребителям:
 тонн – потребителю В1;
тонн – потребителю В1;
 тонн – потребителю В2;
тонн – потребителю В2;
 тонн – потребителю В3;
тонн – потребителю В3;
 тонн – потребителю В4;
тонн – потребителю В4;
 тонн – потребителю В5.
Расстояние между пунктами отправления
и пунктами назначения указаны в таблице.
Стоимость перевозок пропорциональна
количеству груза и расстоянию, на которое
этот груз перевозится.
тонн – потребителю В5.
Расстояние между пунктами отправления
и пунктами назначения указаны в таблице.
Стоимость перевозок пропорциональна
количеству груза и расстоянию, на которое
этот груз перевозится.
Требуется
спланировать перевозки, т. е. указать,
сколько единиц груза должно быть
отправлено от
 поставщика
поставщика потребителю, так, чтобы максимально
удовлетворить спрос потребителей и
чтобы суммарные транспортные затраты
на перевезки были при этом минимальными.
потребителю, так, чтобы максимально
удовлетворить спрос потребителей и
чтобы суммарные транспортные затраты
на перевезки были при этом минимальными.
Указание. Ввиду пропорциональности затрат количеству груза и расстоянию для решения задачи достаточно минимизировать общий объем плана, выраженный в тонно-километрах.
№ 1
 =200;
=200;
 =150;
=150; =150;
=150;
 =90;
=90;
 =100;
=100; =70;
=70; =130;
=130; =110;
=110; .
.
Решение.
Объем
продукции доставленный от поставщика
 потребителю
потребителю зададим
переменной
зададим
переменной .Тогда
план перевозок груза можно записать в
виде матрицы
.Тогда
план перевозок груза можно записать в
виде матрицы

Затраты
на перевозку груза от i-го поставщика
j-му потребителю можно записать как
произведение
 ,
тогда суммарные затраты нареализацию
плана перевозок равны:
,
тогда суммарные затраты нареализацию
плана перевозок равны:
 =
=
 .
.
Цель задачи – минимизировать эти транспортные издержки.
Проверим условие баланса: суммарные потребности потребителей 90+100+70+130+110=500, суммарные запасы продукции всех поставщиков 200+150+150=500. Суммарные потребности потребителей равны суммарным запасам продукции всех поставщиков. Т. е. имеем закрытую задачу.
Опорный план находим методом минимальной стоимости. Ячейки с тарифом 0 заполняем в последнюю очередь. Наименьшим тарифом является 8.


















































































































































































































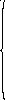








































































|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
12 90 |
15 9 |
21 -2 |
14 5 |
17 110 |
200 |
0 |
|
А2 |
14 0 |
8 100 |
+ 15 -10 |
- 11 50 |
21 2 |
150 |
2 |
|
А3 |
19 4 |
16 7 |
- 26 70 |
+ 12 80 |
20 0 |
150 |
3 |
|
потребности |
90 |
100 |
70 |
130 |
110 |
500 |
|
|
|
12 |
6 |
23 |
9 |
17 |
|
|




Записываем в левый нижний угол клетки А2В2 – 100 ед. продукции. Потребности полностью удовлетворены, столбец В2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 11. Записываем в левый нижний угол клетки А2В4 – 50 ед. продукции. Запасы полностью исчерпаны, строку А2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 12. Записываем в левый нижний угол клетки А1В1 – 90 ед. продукции. Потребности полностью удовлетворены, столбец В1 вычеркиваем. Записываем в левый нижний угол клетки А3В4 – 80 ед. продукции. Потребности полностью удовлетворены, столбец В4 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 17. Записываем в левый нижний угол клетки А1В5 – 110 ед. продукции. Потребности полностью удовлетворены и запасы исчерпаны, столбец В5 и строку А1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 26. Записываем в левый нижний угол клетки А3В3 – 70 ед. продукции. Запасы полностью исчерпаны и потребности полностью удовлетворены. Строку А3 и столбец В3 вычеркиваем.
Число
занятых клеток должно быть равно
 .
В нашем случае число занятых клеток
равно 6. Имеем вырожденный план. Это
произошло из-за того, что при заполнении
клетки А1В5
были вычеркнуты две линии (под линией
понимаем строку или столбец). Занимаем
одну клетку, так чтобы она не составляла
с другими занятыми клетками замкнутый
цикл. Выбираем, А2В1.
.
В нашем случае число занятых клеток
равно 6. Имеем вырожденный план. Это
произошло из-за того, что при заполнении
клетки А1В5
были вычеркнуты две линии (под линией
понимаем строку или столбец). Занимаем
одну клетку, так чтобы она не составляла
с другими занятыми клетками замкнутый
цикл. Выбираем, А2В1.
Полученный таким образом план вырожденный, но занятых клеток нужное количество.
Проверим
полученный опорный план на оптимальность.
Находим потенциалы:
 и
и .
Для каждой базисной переменной
.
Для каждой базисной переменной потенциалы удовлетворяют условию
потенциалы удовлетворяют условию +
+ =
= .
Имеем систему:
.
Имеем систему:



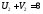



Пусть
 =0,
тогда
=0,
тогда =12
=12
 =2
=2
 =6
=6
 =3
=3
 23
23
 9
9
 17
17
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -10 стоит в
ячейке А2В3.
Ячейка А2В3
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -10 стоит в
ячейке А2В3.
Ячейка А2В3
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 50 к значениям в клетках со
знаком «+» и вычитаем 50 из значений в
клетках со знаком
:
прибавляем 50 к значениям в клетках со
знаком «+» и вычитаем 50 из значений в
клетках со знаком
«-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
+ 12 90 |
15 9 |
21 8 |
14 15 |
- 17 110 |
200 |
0 |
|
А2 |
- 14 0 |
8 100 |
+ 15 50 |
11 10 |
21 2 |
150 |
2 |
|
А3 |
19 4 |
16 -3 |
- 26 20 |
12 130 |
+ 20 -10 |
150 |
13 |
|
потребности |
90 |
100 |
70 |
130 |
110 |
500 |
|
|
|
12 |
6 |
13 |
-1 |
17 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =12
=12
 =2
=2
 =6
=6
 =13
=13
 13
13
 -1
-1
 17
17
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -10 стоит в
ячейке А3В5.
Ячейка А3В5
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -10 стоит в
ячейке А3В5.
Ячейка А3В5
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 0 к значениям в клетках со
знаком «+» и вычитаем 0 из значений в
клетках со знаком «-».
:
прибавляем 0 к значениям в клетках со
знаком «+» и вычитаем 0 из значений в
клетках со знаком «-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
12 90 |
15 -1 |
21 -2 |
14 5 |
17 110 |
200 |
0 |
|
А2 |
14 10 |
- 8 100 |
+ 15 50 |
11 10 |
21 12 |
150 |
-8 |
|
А3 |
19 4 |
+ 16 -3 |
- 26 20 |
12 130 |
20 0 |
150 |
3 |
|
потребности |
90 |
100 |
70 |
130 |
110 |
500 |
|
|
|
12 |
16 |
23 |
9 |
17 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =12
=12
 =-8
=-8
 =16
=16
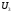 =3
=3
 23
23
 9
9
 17
17
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -3 стоит в
ячейке А3В2.
Ячейка А3В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -3 стоит в
ячейке А3В2.
Ячейка А3В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 20 к значениям в клетках со
знаком «+» и вычитаем 20 из значений в
клетках со знаком
:
прибавляем 20 к значениям в клетках со
знаком «+» и вычитаем 20 из значений в
клетках со знаком
«-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
12 90 |
15 -2 |
21 1 |
14 5 |
17 110 |
200 |
0 |
|
А2 |
14 7 |
8 80 |
15 70 |
11 7 |
21 9 |
150 |
-5 |
|
А3 |
19 4 |
16 20 |
26 3 |
12 130 |
20 0 |
150 |
3 |
|
потребности |
90 |
100 |
70 |
130 |
110 |
500 |
|
|
|
12 |
13 |
20 |
9 |
17 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =12
=12
 =-5
=-5
 =13
=13
 =3
=3
 20
20
 9
9
 17
17
Так как среди оценок для небазисных клеток нет отрицательных, то план оптимален.
Итак, 1-ый поставщик отправляет 90 тонн груза первому потребителю и 110 тонн груза пятому потребителю.
2-ой поставщик отправляет 80 тонн груза второму потребителю и 70 тонн груза третьему потребителю.
3-ий поставщик отправляет 20 тонн груза второму потребителю и 130 тонн груза четвертому потребителю.
Суммарные
затраты при этом
 6520
тонн-километров.
6520
тонн-километров.
№ 2
 =300;
=300;
 =280;
=280; =220;
=220;
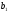 =180;
=180;
 =140;
=140; =190;
=190; =120;
=120; =170;
=170; .
.
Решение.
Объем
продукции доставленный от поставщика
 потребителю
потребителю зададим
переменной
зададим
переменной .Тогда
план перевозок груза можно записать в
виде матрицы
.Тогда
план перевозок груза можно записать в
виде матрицы

Затраты
на перевозку груза от i-го поставщика
j-му потребителю можно записать как
произведение
 ,
тогда суммарные затраты нареализацию
плана перевозок равны:
,
тогда суммарные затраты нареализацию
плана перевозок равны:
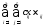 =
=
 .
.
Цель задачи – минимизировать эти транспортные издержки.
Проверим условие баланса: суммарные потребности потребителей 180+140+190+120+170=800, суммарные запасы продукции всех поставщиков 300+280+220=800. Суммарные потребности потребителей равны суммарным запасам продукции всех поставщиков. Т. е. имеем закрытую задачу.
Опорный план находим методом минимальной стоимости. Ячейки с тарифом 0 заполняем в последнюю очередь. Наименьшим тарифом является 9.
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
12 2 |
21 9 |
- 9 190 |
+ 10 110 |
16 10 |
300 |
0 |
|
А2 |
13 180 |
+ 15 90 |
11 -1 |
- 13 10 |
21 12 |
280 |
3 |
|
А3 |
19 -5 |
- 26 50 |
+ 12 -11 |
+ 17 -7 |
20 170 |
220 |
14 |
|
потребности |
180 |
140 |
190 |
120 |
170 |
800 |
|
|
|
10 |
12 |
9 |
10 |
6 |
|
|
Записываем в левый нижний угол клетки А1В3 – 190 ед. продукции. Потребности полностью удовлетворены, столбец В3 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 10. Записываем в левый нижний угол клетки А1В4 – 110 ед. продукции. Запасы полностью исчерпаны, строку А1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 13. Записываем в левый нижний угол клетки А2В1 – 180 ед. продукции. Потребности полностью удовлетворены, столбец В1 вычеркиваем. Записываем в левый нижний угол клетки А2В4 – 10 ед. продукции. Потребности полностью удовлетворены, столбец В4 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 15. Записываем в левый нижний угол клетки А2В2 – 90 ед. продукции. Запасы полностью исчерпаны, строку А2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 20. Записываем в левый нижний угол клетки А3В5 – 170 ед. продукции. Потребности полностью удовлетворены, столбец В5 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 26. Записываем в левый нижний угол клетки А3В2 – 50 ед. продукции. Запасы полностью исчерпаны и потребности полностью удовлетворены. Строку А3 и столбец В2 вычеркиваем.
Число
занятых клеток должно быть равно
 .
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
.
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
Проверим
полученный опорный план на оптимальность.
Находим потенциалы:
 и
и .
Для каждой базисной переменной
.
Для каждой базисной переменной потенциалы удовлетворяют условию
потенциалы удовлетворяют условию +
+ =
= .
Имеем систему:
.
Имеем систему:







Пусть
 =0,
тогда
=0,
тогда =10
=10
 =3
=3
 =12
=12
 =14
=14
 9
9
 10
10
 6
6
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -11 стоит в
ячейке А3В3.
Ячейка А3В3
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -11 стоит в
ячейке А3В3.
Ячейка А3В3
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 50 к значениям в клетках со
знаком «+» и вычитаем 50 из значений в
клетках со знаком
:
прибавляем 50 к значениям в клетках со
знаком «+» и вычитаем 50 из значений в
клетках со знаком
«-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
+ 12 -9 |
21 -2 |
- 9 180 |
10 120 |
16 -1 |
300 |
0 |
|
А2 |
- 13 180 |
+ 15 100 |
11 10 |
13 11 |
21 12 |
280 |
-8 |
|
А3 |
19 -5 |
- 26 40 |
+ 12 10 |
17 4 |
20 170 |
220 |
3 |
|
потребности |
180 |
140 |
190 |
120 |
170 |
800 |
|
|
|
21 |
23 |
9 |
10 |
17 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =21
=21
 =
-8
=
-8
 =23
=23
 =3
=3
 9
9
 10
10
 17
17
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -9 стоит в
ячейке А1В1.
Ячейка А1В1
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -9 стоит в
ячейке А1В1.
Ячейка А1В1
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 40 к значениям в клетках со
знаком «+» и вычитаем 40 из значений в
клетках со знаком «-».
:
прибавляем 40 к значениям в клетках со
знаком «+» и вычитаем 40 из значений в
клетках со знаком «-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
12 40 |
21 7 |
- 9 140 |
10 120 |
+ 16 -1 |
300 |
0 |
|
А2 |
13 140 |
15 140 |
11 1 |
13 2 |
21 3 |
280 |
1 |
|
А3 |
19 4 |
26 9 |
+ 12 50 |
17 4 |
- 20 170 |
220 |
3 |
|
потребности |
180 |
140 |
190 |
120 |
170 |
800 |
|
|
|
12 |
14 |
9 |
10 |
17 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =12
=12
 =1
=1
 =14
=14
 =3
=3
 9
9
 10
10
 17
17
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -1 стоит в
ячейке А1В5.
Ячейка А1В5
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -1 стоит в
ячейке А1В5.
Ячейка А1В5
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 140 к значениям в клетках со
знаком «+» и вычитаем 140 из значений в
клетках со знаком «-».
:
прибавляем 140 к значениям в клетках со
знаком «+» и вычитаем 140 из значений в
клетках со знаком «-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
12 40 |
21 7 |
9 1 |
10 120 |
16 140 |
300 |
0 |
|
А2 |
13 140 |
15 140 |
11 2 |
13 2 |
21 4 |
280 |
1 |
|
А3 |
19 3 |
26 8 |
12 190 |
17 3 |
20 30 |
220 |
4 |
|
потребности |
180 |
140 |
190 |
120 |
170 |
800 |
|
|
|
12 |
14 |
8 |
10 |
16 |
|
|
Проверим полученный опорный план на оптимальность:





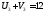

Пусть
 =0,
тогда
=0,
тогда =12
=12
 =1
=1
 =14
=14
 =4
=4
 8
8
 10
10
 16
16
Так как среди оценок для небазисных клеток нет отрицательных, то план оптимален.
Итак, 1-ый поставщик отправляет 40 тонн груза первому потребителю, 120 тонн груза четвертому потребителю и 140 тонн груза пятому потребителю.
2-ой поставщик отправляет 140 тонн груза первому потребителю и 140 тонн груза второму потребителю.
3-ий поставщик отправляет 190 тонн груза третьему потребителю и 30 тонн груза пятому потребителю.
Суммарные
затраты при этом
 10720
тонн-километров.
10720
тонн-километров.
№ 3
 =250;
=250;
 =200;
=200; =150;
=150;
 =180;
=180;
 =120;
=120; =90;
=90; =105;
=105; =105;
=105; .
.
Решение.
Объем
продукции доставленный от поставщика
 потребителю
потребителю зададим
переменной
зададим
переменной .Тогда
план перевозок груза можно записать в
виде матрицы
.Тогда
план перевозок груза можно записать в
виде матрицы

Затраты
на перевозку груза от i-го поставщика
j-му потребителю можно записать как
произведение
 ,
тогда суммарные затраты нареализацию
плана перевозок равны:
,
тогда суммарные затраты нареализацию
плана перевозок равны:
 =
=
 .
.
Цель задачи – минимизировать эти транспортные издержки.
Проверим условие баланса: суммарные потребности потребителей 180+120+90+105+105=600, суммарные запасы продукции всех поставщиков 250+200+150=600. Суммарные потребности потребителей равны суммарным запасам продукции всех поставщиков. Т. е. имеем закрытую задачу.
Опорный план находим методом минимальной стоимости. Ячейки с тарифом 0 заполняем в последнюю очередь. Наименьшим тарифом является 4.
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
12 145 |
8 5 |
21 7 |
10 105 |
15 7 |
250 |
0 |
|
А2 |
- 13 35 |
4 120 |
+ 15 45 |
13 2 |
21 12 |
200 |
1 |
|
А3 |
+ 19 -5 |
16 1 |
- 26 45 |
17 -5 |
20 105 |
150 |
12 |
|
потребности |
180 |
120 |
90 |
105 |
110 |
600 |
|
|
|
12 |
3 |
14 |
10 |
8 |
|
|
Записываем в левый нижний угол клетки А2В2 – 120 ед. продукции. Потребности полностью удовлетворены, столбец В2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 10. Записываем в левый нижний угол клетки А1В4 – 105 ед. продукции. Потребности полностью удовлетворены, столбец В4 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 12. Записываем в левый нижний угол клетки А1В1 – 145 ед. продукции. Запасы полностью исчерпаны, строку А1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 13. Записываем в левый нижний угол клетки А2В1 – 35 ед. продукции. Потребности полностью удовлетворены, столбец В1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 15. Записываем в левый нижний угол клетки А2В3 – 45 ед. продукции. Запасы полностью исчерпаны, строку А2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 20. Записываем в левый нижний угол клетки А3В5 – 105 ед. продукции. Потребности полностью удовлетворены, столбец В5 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 26. Записываем в левый нижний угол клетки А3В3 – 45 ед. продукции. Потребности полностью удовлетворены и запасы исчерпаны, столбец В3 и строку А3 вычеркиваем.
Число
занятых клеток должно быть равно
 .
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
.
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
Проверим
полученный опорный план на оптимальность.
Находим потенциалы:
 и
и .
Для каждой базисной переменной
.
Для каждой базисной переменной потенциалы удовлетворяют условию
потенциалы удовлетворяют условию +
+ =
=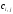 .
Имеем систему:
.
Имеем систему:







Пусть
 =0,
тогда
=0,
тогда =12
=12
 =1
=1
 =3
=3
 =12
=12
 14
14
 10
10
 8
8
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -5 стоит в
ячейке А3В1.
Ячейка А3В1
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -5 стоит в
ячейке А3В1.
Ячейка А3В1
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 35 к значениям в клетках со
знаком «+» и вычитаем 35 из значений в
клетках со знаком «-».
:
прибавляем 35 к значениям в клетках со
знаком «+» и вычитаем 35 из значений в
клетках со знаком «-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
12 145 |
8 5 |
21 2 |
10 105 |
15 2 |
250 |
0 |
|
А2 |
13 5 |
4 120 |
15 80 |
13 7 |
21 12 |
200 |
-4 |
|
А3 |
19 35 |
16 1 |
26 10 |
17 0 |
20 105 |
150 |
7 |
|
потребности |
180 |
120 |
90 |
105 |
110 |
600 |
|
|
|
12 |
8 |
19 |
10 |
13 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда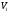 =12
=12
 =-4
=-4
 =8
=8
 =7
=7
 19
19
 10
10
 13
13
Так как среди оценок для небазисных клеток нет отрицательных, то план оптимален.
Итак, 1-ый поставщик отправляет 145 тонн груза первому потребителю и 105 тонн груза четвертому потребителю.
2-ой поставщик отправляет 120 тонн груза второму потребителю и 80 тонн груза третьему потребителю.
3-ий поставщик отправляет 35 тонн груза первому потребителю, 10 тонн груза третьему потребителю и 105 тонн груза пятому потребителю.
Суммарные
затраты при этом
 7495
тонн-километров.
7495
тонн-километров.
№ 4
 =400;
=400;
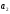 =250;
=250; =350;
=350;
 =200;
=200;
 =170;
=170; =230;
=230; =225;
=225; =175;
=175; .
.
Решение.
Объем
продукции доставленный от поставщика
 потребителю
потребителю зададим
переменной
зададим
переменной .Тогда
план перевозок груза можно записать в
виде матрицы
.Тогда
план перевозок груза можно записать в
виде матрицы

Затраты
на перевозку груза от i-го поставщика
j-му потребителю можно записать как
произведение
 ,
тогда суммарные затраты нареализацию
плана перевозок равны:
,
тогда суммарные затраты нареализацию
плана перевозок равны:
 =
=
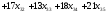 .
.
Цель задачи – минимизировать эти транспортные издержки.
Проверим условие баланса: суммарные потребности потребителей 200+170+230+225+175=1000, суммарные запасы продукции всех поставщиков 400+250+350=1000. Суммарные потребности потребителей равны суммарным запасам продукции всех поставщиков. Т. е. имеем закрытую задачу.
Опорный план находим методом минимальной стоимости. Ячейки с тарифом 0 заполняем в последнюю очередь. Наименьшим тарифом является 5.
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
13 0 |
9 5 |
5 230 |
11 170 |
17 3 |
400 |
0 |
|
А2 |
14 80 |
5 170 |
12 6 |
14 2 |
22 7 |
250 |
1 |
|
А3 |
20 120 |
17 6 |
13 1 |
18 55 |
21 175 |
350 |
7 |
|
потребности |
200 |
170 |
230 |
225 |
175 |
1000 |
|
|
|
13 |
4 |
5 |
11 |
14 |
|
|
Записываем в левый нижний угол клетки А1В3 – 230 ед. продукции. Потребности полностью удовлетворены, столбец В3 вычеркиваем. Записываем в левый нижний угол клетки А2В2 – 170 ед. продукции. Потребности полностью удовлетворены, столбец В2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 11. Записываем в левый нижний угол клетки А1В4 – 170 ед. продукции. Запасы полностью исчерпаны, строку А1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 14. Записываем в левый нижний угол клетки А2В1 – 80 ед. продукции. Запасы полностью исчерпаны, строку А2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 18. Записываем в левый нижний угол клетки А3В4 – 55 ед. продукции. Потребности полностью удовлетворены, столбец В4 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 20. Записываем в левый нижний угол клетки А3В1 – 120 ед. продукции. Потребности полностью удовлетворены, столбец В1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 21. Записываем в левый нижний угол клетки А3В5 – 175 ед. продукции. Потребности полностью удовлетворены и запасы исчерпаны, столбец В5 и строку А3 вычеркиваем.
Число
занятых клеток должно быть равно
 .
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
.
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
Проверим
полученный опорный план на оптимальность.
Находим потенциалы:
 и
и .
Для каждой базисной переменной
.
Для каждой базисной переменной потенциалы удовлетворяют условию
потенциалы удовлетворяют условию +
+ =
= .
Имеем систему:
.
Имеем систему:







Пусть
 =0,
тогда
=0,
тогда =13
=13
 =1
=1
 =4
=4
 =7
=7
 5
5
 11
11
 14.
14.
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок нет отрицательных, то
план оптимален.
.
Оценки запишем в левый нижний угол. Так
как среди оценок нет отрицательных, то
план оптимален.
Итак, 1-ый поставщик отправляет 230 тонн груза третьему потребителю и 170 тонн груза четвертому потребителю.
2-ой поставщик отправляет 80 тонн груза первому потребителю и 170 тонн груза второму потребителю.
3-ий поставщик отправляет 120 тонн груза первому потребителю, 55 тонн груза четвертому потребителю и 175 тонн груза пятому потребителю.
Суммарные
затраты при этом
 12055
тонн-километров.
12055
тонн-километров.
№ 5
 =150;
=150;
 =200;
=200;
 =150;
=150;
 =160;
=160;
 =70;
=70;
 =90;
=90; =80;
=80; =100;
=100;
 .
.
Решение.
Объем
продукции доставленный от поставщика
 потребителю
потребителю зададим
переменной
зададим
переменной .Тогда
план перевозок груза можно записать в
виде матрицы
.Тогда
план перевозок груза можно записать в
виде матрицы

Затраты
на перевозку груза от i-го поставщика
j-му потребителю можно записать как
произведение
 ,
тогда суммарные затраты нареализацию
плана перевозок равны:
,
тогда суммарные затраты нареализацию
плана перевозок равны:
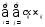 =
=
 .
.
Цель задачи – минимизировать эти транспортные издержки.
Проверим условие баланса: суммарные потребности потребителей 160+70+90+80+100=500, суммарные запасы продукции всех поставщиков 150+200+150=500. Суммарные потребности потребителей равны суммарным запасам продукции всех поставщиков. Т. е. имеем закрытую задачу.
Опорный план находим методом минимальной стоимости. Ячейки с тарифом 0 заполняем в последнюю очередь. Наименьшим тарифом является 4.
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
+ 8 -3 |
20 -1 |
7 90 |
- 11 60 |
16 10 |
150 |
0 |
|
А2 |
- 4 160 |
+ 14 40 |
12 12 |
15 11 |
17 12 |
200 |
-7 |
|
А3 |
15 3 |
- 22 30 |
11 3 |
+ 12 20 |
19 100 |
150 |
1 |
|
потребности |
160 |
70 |
90 |
80 |
100 |
500 |
|
|
|
11 |
21 |
7 |
11 |
18 |
|
|
Записываем в левый нижний угол клетки А2В1 – 160 ед. продукции. Потребности полностью удовлетворены, столбец В1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 7. Записываем в левый нижний угол клетки А1В3 – 90 ед. продукции. Потребности полностью удовлетворены, столбец В3 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 11. Записываем в левый нижний угол клетки А1В4 –60 ед. продукции. Запасы полностью исчерпаны, строку А1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 12. Записываем в левый нижний угол клетки А3В4 –20 ед. продукции. Потребности полностью удовлетворены, столбец В4 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 14. Записываем в левый нижний угол клетки А2В2 – 40 ед. продукции. Запасы полностью исчерпаны, строку А2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 19. Записываем в левый нижний угол клетки А3В5 – 100 ед. продукции. Потребности полностью удовлетворены, столбец В5 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 22. Записываем в левый нижний угол клетки А3В2 – 30 ед. продукции. Запасы полностью исчерпаны и потребности полностью удовлетворены. Строку А3 и столбец В2 вычеркиваем.
Число
занятых клеток должно быть равно
 .
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
.
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
Проверим
полученный опорный план на оптимальность.
Находим потенциалы:
 и
и .
.







Пусть
 =0,
тогда
=0,
тогда =11
=11
 =-7
=-7
 =21
=21
 =1
=1
 7
7
 11
11
 18
18
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -3 стоит в
ячейке А1В1.
Ячейка А1В1
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -3 стоит в
ячейке А1В1.
Ячейка А1В1
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 20 к значениям в клетках со
знаком «+» и вычитаем 20 из значений в
клетках со знаком
:
прибавляем 20 к значениям в клетках со
знаком «+» и вычитаем 20 из значений в
клетках со знаком
«-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
8 30 |
20 2 |
7 90 |
- 11 30 |
+ 16 -2 |
150 |
0 |
|
А2 |
4 130 |
14 70 |
12 9 |
15 8 |
17 3 |
200 |
-4 |
|
А3 |
15 6 |
22 3 |
11 3 |
+ 12 50 |
- 19 100 |
150 |
1 |
|
потребности |
160 |
70 |
90 |
80 |
100 |
500 |
|
|
|
8 |
18 |
7 |
11 |
18 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =8
=8
 =
-4
=
-4
 =18
=18
 =1
=1
 7
7
 11
11
 18
18
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -2 стоит в
ячейке А1В5.
Ячейка А1В5
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -2 стоит в
ячейке А1В5.
Ячейка А1В5
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 30 к значениям в клетках со
знаком «+» и вычитаем 30 из значений в
клетках со знаком «-».
:
прибавляем 30 к значениям в клетках со
знаком «+» и вычитаем 30 из значений в
клетках со знаком «-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
8 30 |
20 2 |
7 90 |
11 2 |
16 30 |
150 |
0 |
|
А2 |
4 130 |
14 70 |
12 9 |
15 10 |
17 5 |
200 |
-4 |
|
А3 |
15 4 |
22 1 |
11 1 |
12 50 |
19 100 |
150 |
3 |
|
потребности |
160 |
70 |
90 |
80 |
100 |
500 |
|
|
|
8 |
18 |
7 |
9 |
16 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =8
=8
 =
-4
=
-4
 =18
=18
 =3
=3
 7
7
 9
9
 16
16
Так как среди оценок для небазисных клеток нет отрицательных, то план оптимален.
Итак, 1-ый поставщик отправляет 30 тонн груза первому потребителю, 90 тонн груза третьему потребителю и 30 тонн груза пятому потребителю.
2-ой поставщик отправляет 130 тонн груза первому потребителю и 70 тонн груза второму потребителю.
3-ий поставщик отправляет 80 тонн груза четвертому потребителю и 70 тонн груза пятому потребителю.
Суммарные затраты при этом
 5140
тонн-километров.
5140
тонн-километров.
№ 6
 =280;
=280;
 =300;
=300; =220;
=220;
 =170;
=170;
 =120;
=120; =190;
=190; =140;
=140; =180;
=180; .
.
Решение.
Объем
продукции доставленный от поставщика
 потребителю
потребителю зададим
переменной
зададим
переменной .Тогда
план перевозок груза можно записать в
виде матрицы
.Тогда
план перевозок груза можно записать в
виде матрицы

Затраты
на перевозку груза от i-го поставщика
j-му потребителю можно записать как
произведение
 ,
тогда суммарные затраты нареализацию
плана перевозок равны:
,
тогда суммарные затраты нареализацию
плана перевозок равны:
 =
=
 .
.
Цель задачи – минимизировать эти транспортные издержки.
Проверим условие баланса: суммарные потребности потребителей 170+120+190+140+180=800, суммарные запасы продукции всех поставщиков 280+300+220=800. Суммарные потребности потребителей равны суммарным запасам продукции всех поставщиков. Т. е. имеем закрытую задачу.
Опорный план находим методом минимальной стоимости. Ячейки с тарифом 0 заполняем в последнюю очередь. Наименьшим тарифом является 3.
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
28 10 |
12 90 |
7 190 |
18 5 |
7 6 |
280 |
0 |
|
А2 |
35 15 |
- 14 30 |
12 3 |
+ 15 90 |
3 180 |
300 |
2 |
|
А3 |
30 170 |
+ 16 -8 |
11 -8 |
- 25 50 |
15 2 |
220 |
12 |
|
потребности |
170 |
120 |
190 |
140 |
180 |
800 |
|
|
|
18 |
12 |
7 |
13 |
1 |
|
|
Записываем в левый нижний угол клетки А2В5 – 180 ед. продукции. Потребности полностью удовлетворены, столбец В5 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 7. Записываем в левый нижний угол клетки А1В3 – 190 ед. продукции. Потребности полностью удовлетворены, столбец В3 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 12. Записываем в левый нижний угол клетки А1В2 –90 ед. продукции. Запасы полностью исчерпаны, строку А1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 14. Записываем в левый нижний угол клетки А2В2 –30 ед. продукции. Потребности полностью удовлетворены, столбец В2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 15. Записываем в левый нижний угол клетки А2В4 – 90 ед. продукции. Запасы полностью исчерпаны, строку А2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 25. Записываем в левый нижний угол клетки А3В4 – 50 ед. продукции. Потребности полностью удовлетворены, столбец В4 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 30. Записываем в левый нижний угол клетки А3В1 – 170 ед. продукции. Запасы полностью исчерпаны и потребности полностью удовлетворены. Строку А3 и столбец В1 вычеркиваем.
Число
занятых клеток должно быть равно
 .
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
.
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
Проверим
полученный опорный план на оптимальность.
Находим потенциалы:
 и
и .
Для каждой базисной переменной
.
Для каждой базисной переменной потенциалы удовлетворяют условию
потенциалы удовлетворяют условию +
+ =
=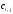 .
.







Пусть
 =0,
тогда
=0,
тогда =18
=18
 =2
=2
 =12
=12
 =12
=12
 7
7
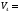 13
13
 1
1
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -8 стоит в
ячейке А3В2.
Ячейка А3В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -8 стоит в
ячейке А3В2.
Ячейка А3В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 30 к значениям в клетках со
знаком «+» и вычитаем 30 из значений в
клетках со знаком
:
прибавляем 30 к значениям в клетках со
знаком «+» и вычитаем 30 из значений в
клетках со знаком
«-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
28 2 |
- 12 90 |
7 190 |
+ 18 -3 |
7 -2 |
280 |
0 |
|
А2 |
35 15 |
14 8 |
12 11 |
15 120 |
3 180 |
300 |
-6 |
|
А3 |
30 170 |
+ 16 30 |
11 0 |
- 25 20 |
15 2 |
220 |
4 |
|
потребности |
170 |
120 |
190 |
140 |
180 |
800 |
|
|
|
26 |
12 |
7 |
21 |
9 |
|
|
Проверим полученный опорный план на оптимальность:


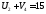




Пусть
 =0,
тогда
=0,
тогда =26
=26
 =-6
=-6
 =12
=12
 =4
=4
 7
7
 21
21
 9
9
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -3 стоит в
ячейке А1В4.
Ячейка А1В4
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -3 стоит в
ячейке А1В4.
Ячейка А1В4
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 20 к значениям в клетках со
знаком «+» и вычитаем 20 из значений в
клетках со знаком «-».
:
прибавляем 20 к значениям в клетках со
знаком «+» и вычитаем 20 из значений в
клетках со знаком «-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
28 2 |
12 70 |
7 190 |
18 20 |
7 1 |
280 |
0 |
|
А2 |
35 12 |
14 5 |
12 8 |
15 120 |
3 180 |
300 |
-3 |
|
А3 |
30 170 |
16 50 |
11 0 |
25 3 |
15 5 |
220 |
4 |
|
потребности |
170 |
120 |
190 |
140 |
180 |
800 |
|
|
|
26 |
12 |
7 |
18 |
6 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
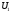 =0,
тогда
=0,
тогда =26
=26
 =-3
=-3
 =12
=12
 =4
=4
 7
7
 18
18
 6
6
Так как среди оценок для небазисных клеток нет отрицательных, то план оптимален.
Итак, 1-ый поставщик отправляет 70 тонн груза второму потребителю, 190 тонн груза третьему потребителю и 20 тонн груза четвертому потребителю.
2-ой поставщик отправляет 120 тонн груза четвертому потребителю и 180 тонн груза пятому потребителю.
3-ий поставщик отправляет 170 тонн груза первому потребителю и 50 тонн груза второму потребителю.
Суммарные затраты при этом
 10770
тонн-километров.
10770
тонн-километров.
№ 7
 =150;
=150;
 =250;
=250; =200;
=200;
 =180;
=180;
 =120;
=120;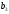 =90;
=90; =105;
=105; =105;
=105; .
.
Решение.
Объем
продукции доставленный от поставщика
 потребителю
потребителю зададим
переменной
зададим
переменной .Тогда
план перевозок груза можно записать в
виде матрицы
.Тогда
план перевозок груза можно записать в
виде матрицы

Затраты
на перевозку груза от i-го поставщика
j-му потребителю можно записать как
произведение
 ,
тогда суммарные затраты нареализацию
плана перевозок равны:
,
тогда суммарные затраты нареализацию
плана перевозок равны:
 =
=
 .
.
Цель задачи – минимизировать эти транспортные издержки.
Проверим условие баланса: суммарные потребности потребителей 180+120+90+105+105=600, суммарные запасы продукции всех поставщиков 150+250+200=600. Суммарные потребности потребителей равны суммарным запасам продукции всех поставщиков. Т. е. имеем закрытую задачу.
Опорный план находим методом минимальной стоимости. Ячейки с тарифом 0 заполняем в последнюю очередь. Наименьшим тарифом является 4.
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
14 2 |
+ 6 -3 |
4 90 |
9 -1 |
- 4 60 |
150 |
0 |
|
А2 |
17 4 |
- 10 120 |
9 4 |
11 85 |
+ 5 45 |
250 |
1 |
|
А3 |
15 180 |
11 -1 |
6 -1 |
13 20 |
8 1 |
200 |
3 |
|
потребности |
180 |
120 |
90 |
105 |
105 |
600 |
|
|
|
12 |
9 |
4 |
10 |
4 |
|
|
Записываем в левый нижний угол клетки А1В3 – 90 ед. продукции. Потребности полностью удовлетворены, столбец В3 вычеркиваем. Записываем в левый нижний угол клетки А1В5 –60 ед. продукции. Запасы полностью исчерпаны, строку А1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 5. Записываем в левый нижний угол клетки А2В5 – 45 ед. продукции. Потребности полностью удовлетворены, столбец В5 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 10. Записываем в левый нижний угол клетки А2В2 –120 ед. продукции. Потребности полностью удовлетворены, столбец В2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 11. Записываем в левый нижний угол клетки А2В4 –85 ед. продукции. Запасы полностью исчерпаны, строку А2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 13. Записываем в левый нижний угол клетки А3В4 –20 ед. продукции. Потребности полностью удовлетворены, столбец В4 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 15. Записываем в левый нижний угол клетки А3В1 – 180 ед. продукции. Запасы полностью исчерпаны и потребности полностью удовлетворены. Строку А3 и столбец В1 вычеркиваем.
Число
занятых клеток должно быть равно
 .
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
.
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
Проверим
полученный опорный план на оптимальность.
Находим потенциалы:
 и
и .
Для каждой базисной переменной
.
Для каждой базисной переменной потенциалы удовлетворяют условию
потенциалы удовлетворяют условию +
+ =
= .
.




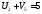


Пусть
 =0,
тогда
=0,
тогда =12
=12
 =1
=1
 =9
=9
 =3
=3
 4
4
 10
10
 4
4
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -3 стоит в
ячейке А1В2.
Ячейка А1В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -3 стоит в
ячейке А1В2.
Ячейка А1В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 60 к значениям в клетках со
знаком «+» и вычитаем 60 из значений в
клетках со знаком
:
прибавляем 60 к значениям в клетках со
знаком «+» и вычитаем 60 из значений в
клетках со знаком
«-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
14 5 |
+ 6 60 |
- 4 90 |
9 2 |
4 3 |
150 |
0 |
|
А2 |
17 4 |
- 10 60 |
9 1 |
+ 11 85 |
5 105 |
250 |
4 |
|
А3 |
15 180 |
11 -1 |
+ 6 -4 |
- 13 20 |
8 1 |
200 |
6 |
|
потребности |
180 |
120 |
90 |
105 |
105 |
600 |
|
|
|
9 |
6 |
4 |
7 |
1 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =9
=9
 =4
=4
 =6
=6
 =6
=6
 4
4
 7
7
 1
1
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -4 стоит в
ячейке А3В3.
Ячейка А3В3
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -4 стоит в
ячейке А3В3.
Ячейка А3В3
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 20 к значениям в клетках со
знаком «+» и вычитаем 20 из значений в
клетках со знаком «-».
:
прибавляем 20 к значениям в клетках со
знаком «+» и вычитаем 20 из значений в
клетках со знаком «-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
14 1 |
6 80 |
4 70 |
9 2 |
4 3 |
150 |
0 |
|
А2 |
17 0 |
10 20 |
9 1 |
11 105 |
5 105 |
250 |
4 |
|
А3 |
15 180 |
11 3 |
6 20 |
13 4 |
8 5 |
200 |
2 |
|
потребности |
180 |
120 |
90 |
105 |
105 |
600 |
|
|
|
13 |
6 |
4 |
7 |
1 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =13
=13
 =4
=4
 =6
=6
 =2
=2
 4
4
 7
7
 1
1
Так как среди оценок для небазисных клеток нет отрицательных, то план оптимален.
Итак, 1-ый поставщик отправляет 80 тонн груза второму потребителю, 70 тонн груза третьему потребителю.
2-ой поставщик отправляет 40 тонн груза второму потребителю, 105 тонн груза четвертому потребителю и 105 тонн груза пятому потребителю.
3-ий поставщик отправляет 180 тонн груза первому потребителю и 20 тонн груза третьему потребителю.
Суммарные затраты при этом
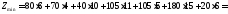 5660
тонн-километров.
5660
тонн-километров.
№ 8
 =250;
=250;
 =400;
=400;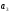 =350;
=350;
 =300;
=300;
 =160;
=160; =220;
=220; =180;
=180; =140;
=140; .
.
Решение.
Объем
продукции доставленный от поставщика
 потребителю
потребителю зададим
переменной
зададим
переменной .Тогда
план перевозок груза можно записать в
виде матрицы
.Тогда
план перевозок груза можно записать в
виде матрицы

Затраты
на перевозку груза от i-го поставщика
j-му потребителю можно записать как
произведение
 ,
тогда суммарные затраты нареализацию
плана перевозок равны:
,
тогда суммарные затраты нареализацию
плана перевозок равны:
 =
=
 .
.
Цель задачи – минимизировать эти транспортные издержки.
Проверим условие баланса: суммарные потребности потребителей 300+160+220+180+140=1000, суммарные запасы продукции всех поставщиков 250+400+350=1000. Суммарные потребности потребителей равны суммарным запасам продукции всех поставщиков. Т. е. имеем закрытую задачу.
Опорный план находим методом минимальной стоимости. Ячейки с тарифом 0 заполняем в последнюю очередь. Наименьшим тарифом является 6.
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
9 250 |
15 3 |
35 2 |
20 -12 |
7 -20 |
250 |
0 |
|
А2 |
15 27 |
35 44 |
+ 12 80 |
- 11 180 |
6 140 |
400 |
-21 |
|
А3 |
16 50 |
19 160 |
- 40 140 |
+ 15 -24 |
25 -9 |
350 |
7 |
|
потребности |
300 |
160 |
220 |
180 |
140 |
1000 |
|
|
|
9 |
12 |
33 |
32 |
27 |
|
|
Записываем в левый нижний угол клетки А2В5 – 140 ед. продукции. Потребности полностью удовлетворены, столбец В5 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 9. Записываем в левый нижний угол клетки А1В1 – 250 ед. продукции. Запасы полностью исчерпаны, строку А1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 11. Записываем в левый нижний угол клетки А2В4 –180 ед. продукции. Потребности полностью удовлетворены, столбец В4 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 12. Записываем в левый нижний угол клетки А2В3 – 80 ед. продукции. Запасы полностью исчерпаны, строку А2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 16. Записываем в левый нижний угол клетки А3В1 – 50 ед. продукции. Потребности полностью удовлетворены, столбец В1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 19. Записываем в левый нижний угол клетки А3В2 – 160 ед. продукции. Потребности полностью удовлетворены, столбец В2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 40. Записываем в левый нижний угол клетки А3В3– 140 ед. продукции. Запасы полностью исчерпаны и потребности полностью удовлетворены. Строку А3 и столбец В3 вычеркиваем.
Число
занятых клеток должно быть равно
 .
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
.
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
Проверим
полученный опорный план на оптимальность.
Находим потенциалы:
 и
и .
Для каждой базисной переменной
.
Для каждой базисной переменной потенциалы удовлетворяют условию
потенциалы удовлетворяют условию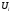 +
+ =
= .
.







Пусть
 =0,
тогда
=0,
тогда =9
=9
 =-21
=-21
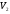 =12
=12
 =7
=7
 33
33
 32
32
 27
27
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -24 стоит в
ячейке А3В4.
Ячейка А3В4
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -24 стоит в
ячейке А3В4.
Ячейка А3В4
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 140 к значениям в клетках со
знаком «+» и вычитаем 140 из значений в
клетках со знаком
:
прибавляем 140 к значениям в клетках со
знаком «+» и вычитаем 140 из значений в
клетках со знаком
«-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
9 250 |
15 3 |
35 26 |
20 12 |
7 4 |
250 |
0 |
|
А2 |
15 3 |
35 20 |
12 220 |
11 40 |
6 140 |
400 |
3 |
|
А3 |
16 50 |
19 160 |
40 24 |
15 140 |
25 15 |
350 |
7 |
|
потребности |
300 |
160 |
220 |
180 |
140 |
1000 |
|
|
|
9 |
12 |
9 |
8 |
3 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =9
=9
 =3
=3
 =12
=12
 =7
=7
 9
9
 8
8
 3
3
Так как среди оценок для небазисных клеток нет отрицательных, то план оптимален.
Итак, 1-ый поставщик отправляет 250 тонн груза первому потребителю
2-ой поставщик отправляет 220 тонн груза третьему потребителю, 40 тонн груза четвертому потребителю и 140 тонн груза пятому потребителю.
3-ий поставщик отправляет 50 тонн груза первому потребителю, 160 тонн груза второму потребителю и 140 тонн груза четвертому потребителю.
Суммарные затраты при этом
 12110
тонн-километров.
12110
тонн-километров.
№ 9
 =150;
=150;
 =150;
=150;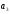 =200;
=200;
 =100;
=100;
 =70;
=70;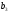 =130;
=130; =110;
=110; =90;
=90; .
.
Решение.
Объем
продукции доставленный от поставщика
 потребителю
потребителю зададим
переменной
зададим
переменной .Тогда
план перевозок груза можно записать в
виде матрицы
.Тогда
план перевозок груза можно записать в
виде матрицы

Затраты
на перевозку груза от i-го поставщика
j-му потребителю можно записать как
произведение
 ,
тогда суммарные затраты нареализацию
плана перевозок равны:
,
тогда суммарные затраты нареализацию
плана перевозок равны:
 =
=
 .
.
Цель задачи – минимизировать эти транспортные издержки.
Проверим условие баланса: суммарные потребности потребителей 100+70+130+110+90=500, суммарные запасы продукции всех поставщиков 150+150+200=500. Суммарные потребности потребителей равны суммарным запасам продукции всех поставщиков. Т. е. имеем закрытую задачу.
Опорный план находим методом минимальной стоимости. Ячейки с тарифом 0 заполняем в последнюю очередь. Наименьшим тарифом является 3.
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
20 19 |
3 70 |
- 9 80 |
15 3 |
+ 35 -6 |
150 |
0 |
|
А2 |
4 100 |
10 4 |
12 50 |
20 5 |
46 2 |
150 |
3 |
|
А3 |
25 17 |
11 1 |
+ 16 0 |
19 110 |
- 48 90 |
200 |
7 |
|
потребности |
100 |
70 |
130 |
110 |
90 |
500 |
|
|
|
1 |
3 |
9 |
12 |
41 |
|
|
Записываем в левый нижний угол клетки А1В2 – 70 ед. продукции. Потребности полностью удовлетворены, столбец В2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 4. Записываем в левый нижний угол клетки А1В2 –100 ед. продукции. Потребности полностью удовлетворены, столбец В1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 9. Записываем в левый нижний угол клетки А1В3 –80 ед. продукции. Запасы полностью исчерпаны, строку А1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 12. Записываем в левый нижний угол клетки А2В3 – 50 ед. продукции. Потребности полностью удовлетворены и запасы исчерпаны. Вычеркиваем столбец В3 и строку А2.
Из оставшихся ячеек наименьшим является тариф 19. Записываем в левый нижний угол клетки А3В4 –110 ед. продукции. Потребности полностью удовлетворены, столбец В4 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 48. Записываем в левый нижний угол клетки А3В5 – 90 ед. продукции. Запасы полностью исчерпаны и потребности полностью удовлетворены. Строку А3 и столбец В5 вычеркиваем.
Число
занятых клеток должно быть равно
 .
В нашем случае число занятых клеток
равно 6. Имеем вырожденный план. Это
произошло из-за того, что при заполнении
клетки А2В3
были вычеркнуты две линии (под линией
понимаем строку или столбец). Занимаем
одну клетку, так чтобы она не составляла
с другими занятыми клетками замкнутый
цикл. Выбираем А3В3.
Полученный план вырожденный, но занятых
клеток нужное количество.
.
В нашем случае число занятых клеток
равно 6. Имеем вырожденный план. Это
произошло из-за того, что при заполнении
клетки А2В3
были вычеркнуты две линии (под линией
понимаем строку или столбец). Занимаем
одну клетку, так чтобы она не составляла
с другими занятыми клетками замкнутый
цикл. Выбираем А3В3.
Полученный план вырожденный, но занятых
клеток нужное количество.
Проверим
полученный опорный план на оптимальность.
Находим потенциалы:
 и
и .
Для каждой базисной переменной
.
Для каждой базисной переменной потенциалы удовлетворяют условию
потенциалы удовлетворяют условию +
+ =
= .
.







Пусть
 =0,
тогда
=0,
тогда =1
=1
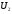 =3
=3
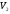 =3
=3
 =7
=7
 9
9
 12
12
 41
41
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -6 стоит в
ячейке А1В5.
Ячейка А1В5
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -6 стоит в
ячейке А1В5.
Ячейка А1В5
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 80 к значениям в клетках со
знаком «+» и вычитаем 80 из значений в
клетках со знаком
:
прибавляем 80 к значениям в клетках со
знаком «+» и вычитаем 80 из значений в
клетках со знаком
«-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
20 25 |
- 3 70 |
9 6 |
15 9 |
+ 35 80 |
150 |
0 |
|
А2 |
4 100 |
10 -2 |
12 50 |
20 5 |
46 2 |
150 |
9 |
|
А3 |
25 17 |
+ 11 -5 |
16 80 |
19 110 |
- 48 10 |
200 |
13 |
|
потребности |
100 |
70 |
130 |
110 |
90 |
500 |
|
|
|
-5 |
3 |
3 |
6 |
35 |
|
|
Проверим полученный опорный план на оптимальность:




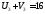


Пусть
 =0,
тогда
=0,
тогда =-5
=-5
 =9
=9
 =3
=3
 =13
=13
 3
3
 6
6
 35
35
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -5 стоит в
ячейке А3В2.
Ячейка А3В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -5 стоит в
ячейке А3В2.
Ячейка А3В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 10 к значениям в клетках со
знаком «+» и вычитаем 10 из значений в
клетках со знаком «-».
:
прибавляем 10 к значениям в клетках со
знаком «+» и вычитаем 10 из значений в
клетках со знаком «-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
20 20 |
3 60 |
9 1 |
15 4 |
35 90 |
150 |
0 |
|
А2 |
4 100 |
10 3 |
12 50 |
20 5 |
46 7 |
150 |
4 |
|
А3 |
25 17 |
11 10 |
16 80 |
19 110 |
48 5 |
200 |
8 |
|
потребности |
100 |
70 |
130 |
110 |
90 |
500 |
|
|
|
0 |
3 |
8 |
11 |
35 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =0
=0
 =4
=4
 =3
=3
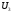 =8
=8
 8
8
 11
11
 35
35
Так как среди оценок для небазисных клеток нет отрицательных, то план оптимален.
Итак, 1-ый поставщик отправляет 60 тонн груза второму потребителю, 90 тонн груза пятому потребителю.
2-ой поставщик отправляет 100 тонн груза первому потребителю, 50 тонн груза третьему потребителю.
3-ий поставщик отправляет 10 тонн груза второму потребителю, 80 тонн груза третьему потребителю и 110 тонн груза четвертому потребителю.
Суммарные затраты при этом
 7810
тонн-километров.
7810
тонн-километров.
№ 10
 =280;
=280;
 =220;
=220; =300;
=300;
 =190;
=190;
 =140;
=140; =180;
=180; =120;
=120; =170;
=170; .
.
Решение.
Объем
продукции доставленный от поставщика
 потребителю
потребителю зададим
переменной
зададим
переменной .Тогда
план перевозок груза можно записать в
виде матрицы
.Тогда
план перевозок груза можно записать в
виде матрицы

Затраты
на перевозку груза от i-го поставщика
j-му потребителю можно записать как
произведение
 ,
тогда суммарные затраты нареализацию
плана перевозок равны:
,
тогда суммарные затраты нареализацию
плана перевозок равны:
 =
=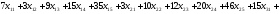
 .
.
Цель задачи – минимизировать эти транспортные издержки.
Проверим условие баланса: суммарные потребности потребителей 190+140+180+120+170=800, суммарные запасы продукции всех поставщиков 280+220+300=800. Суммарные потребности потребителей равны суммарным запасам продукции всех поставщиков. Т. е. имеем закрытую задачу.
Опорный план находим методом минимальной стоимости. Ячейки с тарифом 0 заполняем в последнюю очередь. Наименьшим тарифом является 3.
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
7 15 |
3 140 |
9 16 |
- 15 120 |
+ 35 20 |
280 |
0 |
|
А2 |
3 190 |
10 -4 |
12 8 |
20 -6 |
46 30 |
220 |
11 |
|
А3 |
15 10 |
11 -5 |
6 180 |
+ 19 -9 |
- 48 120 |
300 |
13 |
|
потребности |
190 |
140 |
180 |
120 |
170 |
800 |
|
|
|
-8 |
3 |
-7 |
15 |
35 |
|
|
Записываем в левый нижний угол клетки А1В2 – 140 ед. продукции. Потребности полностью удовлетворены, столбец В2 вычеркиваем.
Записываем в левый нижний угол клетки А2В1 – 190 ед. продукции. Потребности полностью удовлетворены, столбец В1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 6. Записываем в левый нижний угол клетки А3В3 – 180 ед. продукции. Потребности полностью удовлетворены, столбец В3 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 15. Записываем в левый нижний угол клетки А1В4 – 120 ед. продукции. Потребности полностью удовлетворены, столбец В4 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 35. Записываем в левый нижний угол клетки А1В5 – 20 ед. продукции. Запасы полностью исчерпаны, строку А1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 46. Записываем в левый нижний угол клетки А2В5 – 30 ед. продукции. Запасы полностью исчерпаны, строку А2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 48. Записываем в левый нижний угол клетки А3В5 – 120 ед. продукции. Запасы полностью исчерпаны и потребности полностью удовлетворены. Строку А3 и столбец В5 вычеркиваем.
Число
занятых клеток должно быть равно
 .
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
.
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
Проверим
полученный опорный план на оптимальность.
Находим потенциалы:
 и
и .
Для каждой базисной переменной
.
Для каждой базисной переменной потенциалы удовлетворяют условию
потенциалы удовлетворяют условию +
+ =
= .
Имеем систему:
.
Имеем систему:







Пусть
 =0,
тогда
=0,
тогда =-8
=-8
 =11
=11
 =3
=3
 =13
=13
 -7
-7
 15
15
 35
35
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -9 стоит в
ячейке А3В4.
Ячейка А3В4
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -9 стоит в
ячейке А3В4.
Ячейка А3В4
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 120 к значениям в клетках со
знаком «+» и вычитаем 120 из значений в
клетках со знаком
:
прибавляем 120 к значениям в клетках со
знаком «+» и вычитаем 120 из значений в
клетках со знаком
«-». Так как освобождаются две клетки, то в одной из них оставим 0.
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
7 15 |
- 3 140 |
9 16 |
15 9 |
+ 35 140 |
280 |
0 |
|
А2 |
3 190 |
10 -4 |
12 8 |
20 3 |
46 30 |
220 |
11 |
|
А3 |
15 10 |
+ 11 -5 |
6 180 |
19 120 |
- 48 0 |
300 |
13 |
|
потребности |
190 |
140 |
180 |
120 |
170 |
800 |
|
|
|
-8 |
3 |
-7 |
6 |
35 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =-8
=-8
 =11
=11
 =3
=3
 =13
=13
 -7
-7
 6
6
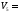 35
35
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -5 стоит в
ячейке А3В2.
Ячейка А3В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+». Выбираем
наименьшее значение из клеток со знаком
«-»
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -5 стоит в
ячейке А3В2.
Ячейка А3В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+». Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 0 к значениям в клетках со
знаком «+» и вычитаем 0 из значений в
клетках со знаком «-».
:
прибавляем 0 к значениям в клетках со
знаком «+» и вычитаем 0 из значений в
клетках со знаком «-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
7 15 |
- 3 140 |
9 11 |
15 4 |
+ 35 140 |
280 |
0 |
|
А2 |
3 190 |
+ 10 -4 |
12 3 |
20 -2 |
- 46 30 |
220 |
11 |
|
А3 |
15 15 |
11 0 |
6 180 |
19 120 |
48 5 |
300 |
8 |
|
потребности |
190 |
140 |
180 |
120 |
170 |
800 |
|
|
|
-8 |
3 |
-2 |
11 |
35 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =-8
=-8
 =11
=11
 =3
=3
 =8
=8
 -2
-2
 11
11
 35
35
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -4 стоит в
ячейке А2В2.
Ячейка А2В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -4 стоит в
ячейке А2В2.
Ячейка А2В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 30 к значениям в клетках со
знаком «+» и вычитаем 30 из значений в
клетках со знаком «-».
:
прибавляем 30 к значениям в клетках со
знаком «+» и вычитаем 30 из значений в
клетках со знаком «-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
7 11 |
3 110 |
9 11 |
15 4 |
35 140 |
280 |
0 |
|
А2 |
3 190 |
10 30 |
12 7 |
20 2 |
46 4 |
220 |
7 |
|
А3 |
15 9 |
11 0 |
6 180 |
19 120 |
48 5 |
300 |
8 |
|
потребности |
190 |
140 |
180 |
120 |
170 |
800 |
|
|
|
-4 |
3 |
-2 |
11 |
35 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =-4
=-4
 =7
=7
 =3
=3
 =8
=8
 -2
-2
 11
11
 35
35
Так как среди оценок для небазисных клеток нет отрицательных, то план оптимален.
Итак, 1-ый поставщик отправляет 110 тонн груза второму потребителю, 170 тонн груза пятому потребителю.
2-ой поставщик отправляет 190 тонн груза первому потребителю и 30 тонн груза второму потребителю.
3-ий поставщик отправляет 180 тонн груза третьему потребителю и 120 тонн груза четвертому потребителю.
Суммарные затраты при этом
 10510
тонн-километров.
10510
тонн-километров.
№ 11
 =200;
=200;
 =250;
=250; =150;
=150;
 =120;
=120;
 =180;
=180; =105;
=105; =90;
=90; =105;
=105; .
.
Решение.
Объем
продукции доставленный от поставщика
 потребителю
потребителю зададим
переменной
зададим
переменной .Тогда
план перевозок груза можно записать в
виде матрицы
.Тогда
план перевозок груза можно записать в
виде матрицы

Затраты
на перевозку груза от i-го поставщика
j-му потребителю можно записать как
произведение
 ,
тогда суммарные затраты нареализацию
плана перевозок равны:
,
тогда суммарные затраты нареализацию
плана перевозок равны:
 =
=
 .
.
Цель задачи – минимизировать эти транспортные издержки.
Проверим условие баланса: суммарные потребности потребителей 120+180+105+90+105=600, суммарные запасы продукции всех поставщиков 200+250+150=600. Суммарные потребности потребителей равны суммарным запасам продукции всех поставщиков. Т. е. имеем закрытую задачу.
Опорный план находим методом минимальной стоимости. Ячейки с тарифом 0 заполняем в последнюю очередь. Наименьшим тарифом является 4.
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
9 1 |
+ 6 -4 |
17 105 |
- 11 20 |
8 75 |
200 |
0 |
|
А2 |
13 11 |
- 4 180 |
9 -2 |
+ 5 70 |
7 5 |
250 |
-6 |
|
А3 |
6 120 |
7 -1 |
14 -1 |
10 1 |
6 30 |
150 |
-2 |
|
потребности |
120 |
180 |
105 |
105 |
105 |
600 |
|
|
|
8 |
10 |
17 |
11 |
8 |
|
|
Записываем в левый нижний угол клетки А2В2 – 180 ед. продукции. Потребности полностью удовлетворены, столбец В2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 5. Записываем в левый нижний угол клетки А2В4 – 70 ед. продукции. Запасы полностью исчерпаны, строку А2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 6. Записываем в левый нижний угол клетки А3В1 – 120 ед. продукции. Потребности полностью удовлетворены, столбец В1 вычеркиваем. Записываем в левый нижний угол клетки А3В5 – 30 ед. продукции. Запасы полностью исчерпаны, строку А3 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 8. Записываем в левый нижний угол клетки А1В5 –75 ед. продукции. Потребности полностью удовлетворены, столбец В5 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 11. Записываем в левый нижний угол клетки А1В4 –20 ед. продукции. Потребности полностью удовлетворены, столбец В4 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 17. Записываем в левый нижний угол клетки А1В3 – 105 ед. продукции. Запасы полностью исчерпаны и потребности полностью удовлетворены. Строку А1 и столбец В3 вычеркиваем.
Число
занятых клеток должно быть равно
 .
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
.
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
Проверим
полученный опорный план на оптимальность.
Находим потенциалы:
 и
и .
Для каждой базисной переменной
.
Для каждой базисной переменной потенциалы удовлетворяют условию
потенциалы удовлетворяют условию +
+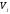 =
= .
.







Пусть
 =0,
тогда
=0,
тогда =8
=8
 =-6
=-6
 =10
=10
 =-2
=-2
 17
17
 11
11
 8
8
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -4 стоит в
ячейке А1В2.
Ячейка А1В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -4 стоит в
ячейке А1В2.
Ячейка А1В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 20 к значениям в клетках со
знаком «+» и вычитаем 20 из значений в
клетках со знаком
:
прибавляем 20 к значениям в клетках со
знаком «+» и вычитаем 20 из значений в
клетках со знаком
«-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
9 1 |
+ 6 20 |
+ 17 105 |
11 4 |
8 75 |
200 |
0 |
|
А2 |
13 7 |
- 4 160 |
+ 9 -6 |
5 70 |
7 1 |
250 |
-2 |
|
А3 |
6 120 |
7 3 |
14 -1 |
10 5 |
6 30 |
150 |
-2 |
|
потребности |
120 |
180 |
105 |
105 |
105 |
600 |
|
|
|
8 |
6 |
17 |
7 |
8 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =8
=8
 =-2
=-2
 =6
=6
 =-2
=-2
 17
17
 7
7
 8
8
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -6 стоит в
ячейке А2В3.
Ячейка А2В3
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -6 стоит в
ячейке А2В3.
Ячейка А2В3
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 105 к значениям в клетках со
знаком «+» и вычитаем 105 из значений в
клетках со знаком «-».
:
прибавляем 105 к значениям в клетках со
знаком «+» и вычитаем 105 из значений в
клетках со знаком «-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
9 1 |
6 125 |
17 6 |
11 4 |
8 75 |
200 |
0 |
|
А2 |
13 7 |
4 55 |
9 105 |
5 70 |
7 1 |
250 |
-2 |
|
А3 |
6 120 |
7 3 |
14 5 |
10 5 |
6 30 |
150 |
-2 |
|
потребности |
120 |
180 |
105 |
105 |
105 |
600 |
|
|
|
8 |
6 |
11 |
7 |
8 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =8
=8
 =-2
=-2
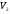 =6
=6
 =-2
=-2
 11
11
 7
7
 8
8
Так как среди оценок для небазисных клеток нет отрицательных, то план оптимален.
Итак, 1-ый поставщик отправляет 125 тонн груза второму потребителю, 75 тонн груза пятому потребителю.
2-ой поставщик отправляет 55 тонн груза второму потребителю, 105 тонн груза третьему потребителю и 90 тонн груза четвертому потребителю.
3-ий поставщик отправляет 120 тонн груза первому потребителю и 30 тонн груза пятому потребителю.
Суммарные затраты при этом
 3865
тонн-километров.
3865
тонн-километров.
№ 12
 =350;
=350;
 =400;
=400; =250;
=250;
 =175;
=175;
 =225;
=225; =230;
=230; =170;
=170; =200;
=200; .
.
Решение.
Объем
продукции доставленный от поставщика
 потребителю
потребителю зададим
переменной
зададим
переменной .Тогда
план перевозок груза можно записать в
виде матрицы
.Тогда
план перевозок груза можно записать в
виде матрицы

Затраты
на перевозку груза от i-го поставщика
j-му потребителю можно записать как
произведение
 ,
тогда суммарные затраты нареализацию
плана перевозок равны:
,
тогда суммарные затраты нареализацию
плана перевозок равны:
 =
=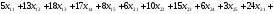
 .
.
Цель задачи – минимизировать эти транспортные издержки.
Проверим условие баланса: суммарные потребности потребителей 175+225+230+170+200=1000, суммарные запасы продукции всех поставщиков 350+400+250=1000. Суммарные потребности потребителей равны суммарным запасам продукции всех поставщиков. Т. е. имеем закрытую задачу.
Опорный план находим методом минимальной стоимости. Ячейки с тарифом 0 заполняем в последнюю очередь. Наименьшим тарифом является 3.
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
5 175 |
13 175 |
18 17 |
17 8 |
8 2 |
350 |
0 |
|
А2 |
6 4 |
+ 10 30 |
15 17 |
- 6 170 |
3 200 |
400 |
-3 |
|
А3 |
24 11 |
- 21 20 |
9 230 |
+ 16 -1 |
17 3 |
250 |
8 |
|
потребности |
175 |
225 |
230 |
170 |
200 |
1000 |
|
|
|
5 |
13 |
1 |
9 |
6 |
|
|
Записываем в левый нижний угол клетки А2В5 – 200 ед. продукции. Потребности полностью удовлетворены, столбец В5 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 5. Записываем в левый нижний угол клетки А1В1 – 175 ед. продукции. Потребности полностью удовлетворены, столбец В1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 6. Записываем в левый нижний угол клетки А2В4 – 170 ед. продукции. Потребности полностью удовлетворены, столбец В4 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 9. Записываем в левый нижний угол клетки А3В3 – 230 ед. продукции. Потребности полностью удовлетворены, столбец В3 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 10. Записываем в левый нижний угол клетки А2В2– 30 ед. продукции. Запасы полностью исчерпаны, строку А2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 13. Записываем в левый нижний угол клетки А1В2– 175 ед. продукции. Запасы полностью исчерпаны, строку А1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 21. Записываем в левый нижний угол клетки А3В2– 20 ед. продукции. Запасы полностью исчерпаны и потребности полностью удовлетворены. Строку А3 и столбец В2 вычеркиваем.
Число
занятых клеток должно быть равно
 .
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
.
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
Проверим
полученный опорный план на оптимальность.
Находим потенциалы:
 и
и .
Для каждой базисной переменной
.
Для каждой базисной переменной потенциалы удовлетворяют условию
потенциалы удовлетворяют условию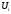 +
+ =
= .
.







Пусть
 =0,
тогда
=0,
тогда =5
=5
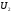 =-3
=-3
 =13
=13
 =8
=8
 1
1
 9
9
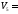 6
6
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -1 стоит в
ячейке А3В4.
Ячейка А3В4
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -1 стоит в
ячейке А3В4.
Ячейка А3В4
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 20 к значениям в клетках со
знаком «+» и вычитаем 20 из значений в
клетках со знаком
:
прибавляем 20 к значениям в клетках со
знаком «+» и вычитаем 20 из значений в
клетках со знаком
«-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
5 175 |
13 175 |
18 16 |
17 8 |
8 2 |
350 |
0 |
|
А2 |
6 4 |
10 50 |
15 16 |
6 150 |
3 200 |
400 |
-3 |
|
А3 |
24 12 |
21 1 |
9 230 |
16 20 |
17 4 |
250 |
7 |
|
потребности |
175 |
225 |
230 |
170 |
200 |
1000 |
|
|
|
5 |
13 |
2 |
9 |
6 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда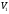 =5
=5
 =-3
=-3
 =13
=13
 =7
=7
 2
2
 9
9
 6
6
Так как среди оценок для небазисных клеток нет отрицательных, то план оптимален.
Итак, 1-ый поставщик отправляет 175 тонн груза первому потребителю и 175 тонн груза второму потребителю
2-ой поставщик отправляет 50 тонн груза второму потребителю, 150 тонн груза четвертому потребителю и 200 тонн груза пятому потребителю.
3-ий поставщик отправляет 230 тонн груза третьему потребителю и 20 тонн груза четвертому потребителю.
Суммарные затраты при этом
 7540
тонн-километров.
7540
тонн-километров.
№ 13
 =250;
=250;
 =250;
=250; =200;
=200;
 =120;
=120;
 =110;
=110;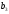 =85;
=85; =195;
=195; =190;
=190; .
.
Решение.
Объем
продукции доставленный от поставщика
 потребителю
потребителю зададим
переменной
зададим
переменной .Тогда
план перевозок груза можно записать в
виде матрицы
.Тогда
план перевозок груза можно записать в
виде матрицы

Затраты
на перевозку груза от i-го поставщика
j-му потребителю можно записать как
произведение
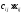 ,
тогда суммарные затраты нареализацию
плана перевозок равны:
,
тогда суммарные затраты нареализацию
плана перевозок равны:
 =
=
 .
.
Цель задачи – минимизировать эти транспортные издержки.
Проверим условие баланса: суммарные потребности потребителей 120+110+85+195+190=700, суммарные запасы продукции всех поставщиков 250+250+200=700. Суммарные потребности потребителей равны суммарным запасам продукции всех поставщиков. Т. е. имеем закрытую задачу.
Опорный план находим методом минимальной стоимости. Ячейки с тарифом 0 заполняем в последнюю очередь. Наименьшим тарифом является 2.
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
13 10 |
7 110 |
16 5 |
+ 4 115 |
- 11 25 |
250 |
0 |
|
А2 |
20 19 |
9 4 |
9 85 |
10 8 |
9 165 |
250 |
-2 |
|
А3 |
2 120 |
4 -2 |
7 -3 |
- 3 80 |
+ 6 -4 |
200 |
-1 |
|
потребности |
120 |
110 |
85 |
195 |
190 |
700 |
|
|
|
3 |
7 |
11 |
4 |
11 |
|
|
Записываем в левый нижний угол клетки А3В1 – 120 ед. продукции. Потребности полностью удовлетворены, столбец В1 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 3. Записываем в левый нижний угол клетки А3В4 – 80 ед. продукции. Запасы полностью исчерпаны, строку А3 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 4. Записываем в левый нижний угол клетки А1В4 – 115 ед. продукции. Потребности полностью удовлетворены, столбец В3 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 7. Записываем в левый нижний угол клетки А1В2 –110 ед. продукции. Потребности полностью удовлетворены, столбец В2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 9. Записываем в левый нижний угол клетки А2В3 –85 ед. продукции. Потребности полностью удовлетворены, столбец В3 вычеркиваем. Записываем в левый нижний угол клетки А2В5 – 165 ед. продукции. Запасы полностью исчерпаны, строку А2 вычеркиваем.
Из оставшихся ячеек наименьшим является тариф 11. Записываем в левый нижний угол клетки А1В5 – 25 ед. продукции. Запасы полностью исчерпаны и потребности полностью удовлетворены. Строку А1 и столбец В5 вычеркиваем.
Число
занятых клеток должно быть равно
 .
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
.
В нашем случае число занятых клеток
равно 7. Имеем не вырожденный план.
Проверим
полученный опорный план на оптимальность.
Находим потенциалы:
 и
и .
Для каждой базисной переменной
.
Для каждой базисной переменной потенциалы удовлетворяют условию
потенциалы удовлетворяют условию +
+ =
= .
.



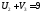



Пусть
 =0,
тогда
=0,
тогда =3
=3
 =-2
=-2
 =7
=7
 =-1
=-1
 11
11
 4
4
 11
11
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -4 стоит в
ячейке А3В5.
Ячейка А3В5
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -4 стоит в
ячейке А3В5.
Ячейка А3В5
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 25 к значениям в клетках со
знаком «+» и вычитаем 25 из значений в
клетках со знаком
:
прибавляем 25 к значениям в клетках со
знаком «+» и вычитаем 25 из значений в
клетках со знаком
«-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
13 10 |
- 7 110 |
16 9 |
+ 4 140 |
11 4 |
250 |
0 |
|
А2 |
20 15 |
9 0 |
9 85 |
10 4 |
9 165 |
250 |
2 |
|
А3 |
2 120 |
+ 4 -2 |
7 1 |
- 3 55 |
6 25 |
200 |
-1 |
|
потребности |
120 |
110 |
85 |
195 |
190 |
700 |
|
|
|
3 |
7 |
7 |
4 |
7 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда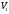 =3
=3
 =2
=2
 =7
=7
 =-1
=-1
 7
7
 4
4
 7
7
Теперь
для небазисных клеток найдем оценки
 .
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -2 стоит в
ячейке А3В2.
Ячейка А3В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
.
Оценки запишем в левый нижний угол. Так
как среди оценок есть отрицательные,
то план не оптимален. Наибольшая по
модулю отрицательная оценка -2 стоит в
ячейке А3В2.
Ячейка А3В2
становится опорной, строим замкнутый
контур с вершинами в загруженных клетках.
Присваиваем клеткам в вершинах контура
поочередно по часовой стрелке знаки
«+» и «-», начиная с опорной клетки,
которой присваиваем знак «+».
Выбираем
наименьшее значение из клеток со знаком
«-»
 :
прибавляем 55 к значениям в клетках со
знаком «+» и вычитаем 55 из значений в
клетках со знаком «-».
:
прибавляем 55 к значениям в клетках со
знаком «+» и вычитаем 55 из значений в
клетках со знаком «-».
|
|
В1 |
В2 |
В3 |
В4 |
В5 |
запасы |
|
|
А1 |
13 8 |
7 55 |
16 7 |
4 140 |
11 2 |
250 |
0 |
|
А2 |
20 15 |
9 2 |
9 85 |
10 6 |
9 165 |
250 |
0 |
|
А3 |
2 120 |
4 55 |
7 1 |
3 2 |
6 25 |
200 |
-3 |
|
потребности |
120 |
110 |
85 |
195 |
190 |
700 |
|
|
|
5 |
7 |
9 |
4 |
9 |
|
|
Проверим полученный опорный план на оптимальность:







Пусть
 =0,
тогда
=0,
тогда =5
=5
 =0
=0
 =7
=7
 =-3
=-3
 9
9
 4
4
 9
9
Так как среди оценок для небазисных клеток нет отрицательных, то план оптимален.
Итак, 1-ый поставщик отправляет 55 тонн груза второму потребителю, 195 тонн груза четвертому потребителю.
2-ой поставщик отправляет 85 тонн груза третьему потребителю и 165 тонн груза пятому потребителю.
3-ий поставщик отправляет 120 тонн груза первому потребителю, 55 тонн груза второму потребителю и 25 тонн груза пятому потребителю.
Суммарные затраты при этом
 4025
тонн-километров.
4025
тонн-километров.