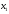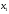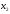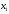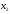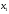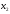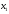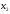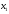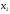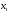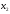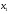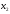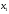Задачи 11-20
Для
сохранения здоровья и работоспособности
человек должен в сутки потреблять не
менее
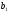 усл. ед. белков, не менее
усл. ед. белков, не менее усл. ед. жиров, не менее
усл. ед. жиров, не менее усл. ед. углеводов. Имеется два вида
продуктов П1
и П2:
стоимость единицы каждого из них равна
соответственно С1
и С2
ден. ед.
усл. ед. углеводов. Имеется два вида
продуктов П1
и П2:
стоимость единицы каждого из них равна
соответственно С1
и С2
ден. ед.
Имеется
матрица А= , в которой
, в которой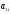 равно количеству усл. ед. белков в единице
продукта
равно количеству усл. ед. белков в единице
продукта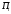 ,
, равно количеству усл. ед. жиров в единице
продукта
равно количеству усл. ед. жиров в единице
продукта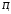 ,
,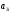 равно количеству усл. ед. углеводов в
единице продукта
равно количеству усл. ед. углеводов в
единице продукта ,
,
Требуется: составить математическую модель задачи, позволяющую сформировать из продуктов П1 и П2 суточную диету, которая содержала бы белков, жиров и углеводов не менее минимальных обоснованных норм и требовала бы минимальных денежных затрат; решить задачу графическим способом.
№ 11
 =20,
=20,
 =40,
=40,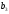 =88,
С1=6,
С2=10,
А=
=88,
С1=6,
С2=10,
А= .
.
Решение.
Данные задачи представим в таблице:
|
Питательные вещества |
Продукты |
Необходимое количество | ||
|
П1 |
П2 | |||
|
белки |
4 |
1 |
20 | |
|
жиры |
4 |
3 |
40 | |
|
углеводы |
4 |
15 |
88 | |
|
Цена |
6 |
10 |
| |
|
количество |
|
|
| |
Пусть
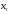 - количество единиц продукта П1,
- количество единиц продукта П1,
 - количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
- количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
С
учетом цены за каждую единицу продукта,
покупателю необходимо будет заплатить
следующую сумму: z=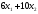 денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
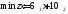
Продукты
необходимо закупить в таком количестве,
чтобы обеспечить организм необходимым
количеством питательных веществ, т. е.
переменные
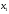 ,
,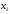 должны удовлетворять ограничениям.
должны удовлетворять ограничениям.
В
одной единице продукта П1
содержится 4 усл. ед. белка, тогда в х1
единицах содержится
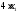 единиц белка. В одной единице продукта
П2
содержится 1 усл. ед. белка, тогда в х2
единицах содержится
единиц белка. В одной единице продукта
П2
содержится 1 усл. ед. белка, тогда в х2
единицах содержится
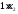 усл. ед. белка.
усл. ед. белка.
Тогда
суммарное количество усл. ед. белка в
рационе равно
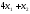 .
.
В
организме же белка должно быть не меньше
необходимого количества, т. е. не меньше
20. Получим первое ограничение
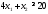 .
.
Рассуждая
аналогично, и просматривая строку «жиры»
данной таблицы, получим второе ограничение:

Просматривая
строку «углеводы» данной таблицы,
получим третье ограничение:
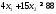
Учтем,
что переменные
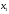 ,
,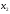 должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
Математическая модель исходной задачи имеет вид:
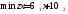
 ,
,
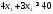 ,
,
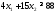 ,
,
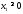 ,
,
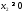 .
.
Строим в прямоугольной декартовой системе координат прямые.
1.
 .
.
|
х1 |
3 |
5 |
|
х2 |
8 |
0 |
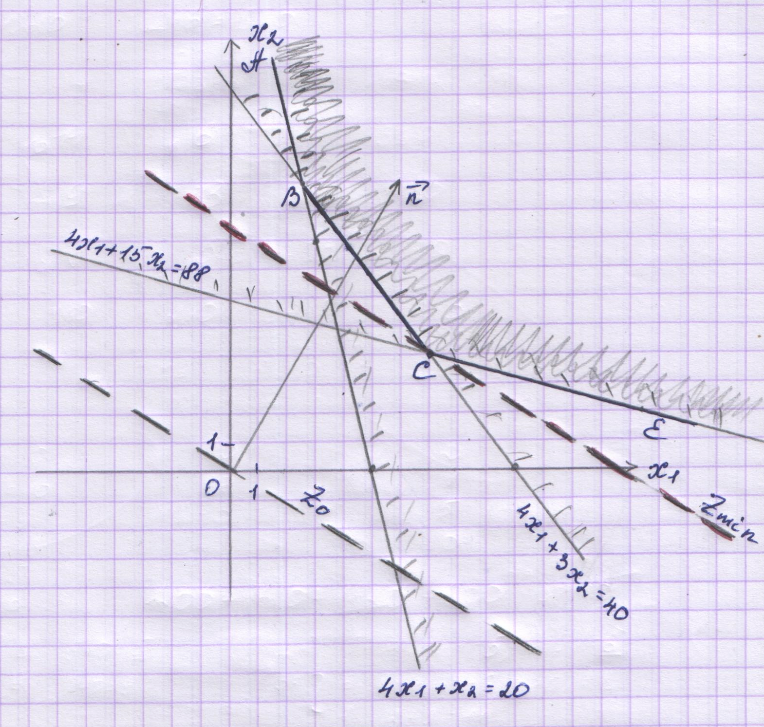
2.
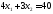 .
.
|
х1 |
2,5 |
10 |
|
х2 |
10 |
0 |
3.
 .
.
|
х1 |
7 |
14,5 |
|
х2 |
4 |
2 |
Каждая из этих прямых разбивает плоскость на две полуплоскости. Только одна из полуплоскостей является решением соответствующего неравенства. Пересечение решений трех неравенств является решением системы – многоугольником решений.
Возьмем точку (1; 1) и подставим в каждое неравенство системы.
1.
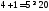 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства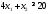 .
.
2.
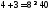 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства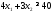 .
.
3.
 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства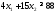 .
.
Учтем,
что
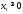 ,
,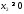 .
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
.
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
Строим
вектор
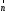 с началом в точке (0; 0) и концов в точке
(6; 10). Перпендикулярно вектору
с началом в точке (0; 0) и концов в точке
(6; 10). Перпендикулярно вектору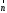 проводим прямую
проводим прямую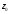 .
.
Необходимо
получить минимум функции цели, т. е.
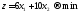 .
Параллельным переносом передвигаем
прямую
.
Параллельным переносом передвигаем
прямую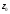 до тех пор пока весь многоугольник не
окажется сверху. В точке С пересеклись
две прямые:
до тех пор пока весь многоугольник не
окажется сверху. В точке С пересеклись
две прямые: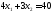 и
и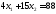 .
Следовательно, координаты точки С
находим из системы уравнений этих
прямых.
.
Следовательно, координаты точки С
находим из системы уравнений этих
прямых.
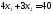 ,
,
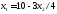 ,
,
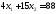 ;
;
 .
.
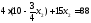
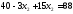

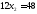
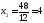
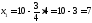
Получили С (7; 4)
Подставляя координаты точки С в уравнение функции цели, получим:
Zmin=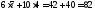 .
.
Ответ: необходимо купить 7 ед. продукта П1 и 4 ед. продукта П2, минимальные денежные затраты равны 82 ден. ед.
№ 12
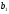 =69,
=69,
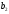 =84,
=84,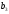 =39,
С1=4,
С2=12,
А=
=39,
С1=4,
С2=12,
А= .
.
Решение.
Данные задачи представим в таблице:
|
Питательные вещества |
Продукты |
Необходимое количество | ||
|
П1 |
П2 | |||
|
белки |
3 |
16 |
69 | |
|
жиры |
21 |
4 |
84 | |
|
углеводы |
3 |
6 |
39 | |
|
Цена |
4 |
12 |
| |
|
количество |
|
|
| |
Пусть
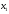 - количество единиц продукта П1,
- количество единиц продукта П1,
 - количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
- количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
С
учетом цены за каждую единицу продукта,
покупателю необходимо будет заплатить
следующую сумму: z=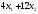 денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
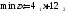
Продукты
необходимо закупить в таком количестве,
чтобы обеспечить организм необходимым
количеством питательных веществ, т. е.
переменные
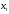 ,
,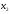 должны удовлетворять ограничениям.
должны удовлетворять ограничениям.
В
одной единице продукта П1
содержится 3 усл. ед. белка, тогда в х1
единицах содержится
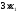 единиц белка. В одной единице продукта
П2
содержится 16 усл. ед. белка, тогда в х2
единицах содержится
единиц белка. В одной единице продукта
П2
содержится 16 усл. ед. белка, тогда в х2
единицах содержится
 усл. ед. белка.
усл. ед. белка.
Тогда
суммарное количество усл. ед. белка в
рационе равно
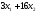 .
.
В
организме же белка должно быть не меньше
необходимого количества, т. е. не меньше
69. Получим первое ограничение
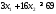 .
.
Рассуждая
аналогично, и просматривая строку «жиры»
данной таблицы, получим второе ограничение:
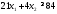
Просматривая
строку «углеводы» данной таблицы,
получим третье ограничение:

Учтем,
что переменные
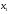 ,
, должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
Математическая модель исходной задачи имеет вид:
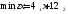
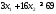 ,
,
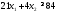 ,
,
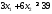 ,
,
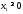 ,
,
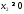 .
.
Строим в прямоугольной декартовой системе координат прямые.
1.
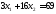 .
.
|
х1 |
7 |
3 |
|
х2 |
3 |
3,75 |
2.
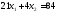 .
.
|
х1 |
4 |
3 |
|
х2 |
0 |
5,25 |
3.
 .
.
|
х1 |
0 |
13 |
|
х2 |
6,5 |
0 |
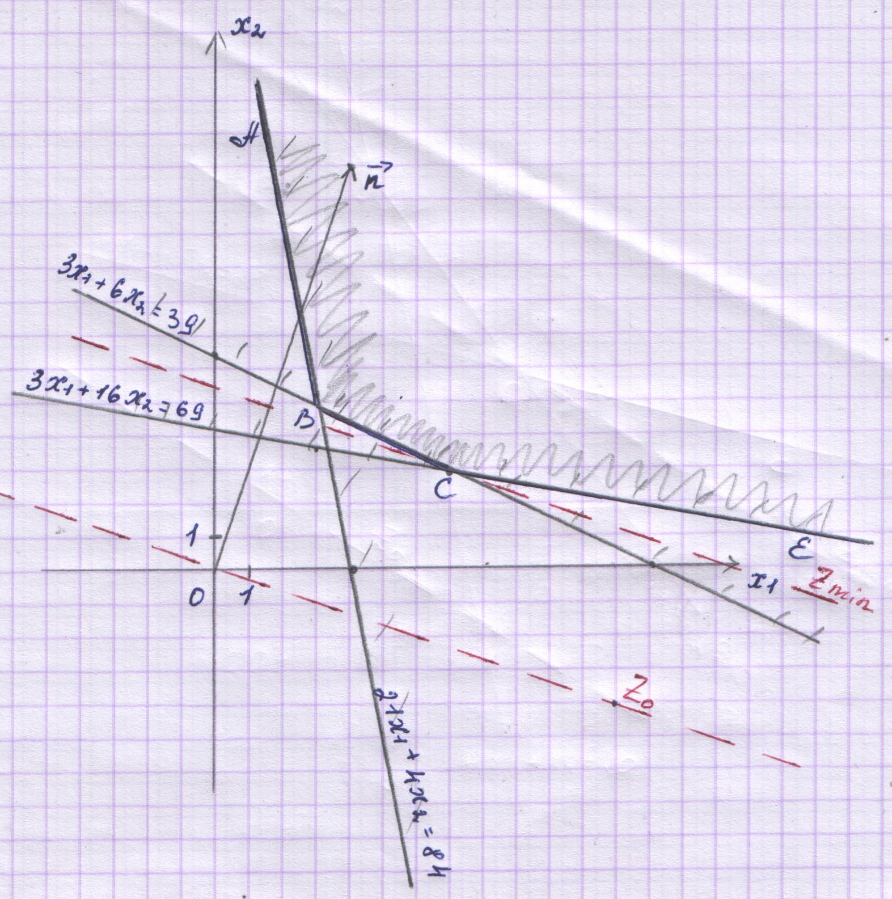
Каждая из этих прямых разбивает плоскость на две полуплоскости. Только одна из полуплоскостей является решением соответствующего неравенства. Пересечение решений трех неравенств является решением системы – многоугольником решений.
Возьмем точку (1; 1) и подставим в каждое неравенство системы.
1.
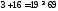 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства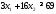 .
.
2.
 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства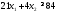 .
.
3.
 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства .
.
Учтем,
что
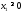 ,
,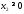 .
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
.
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
Строим
вектор
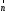 с началом в точке (0; 0) и концов в точке
(4; 12). Перпендикулярно вектору
с началом в точке (0; 0) и концов в точке
(4; 12). Перпендикулярно вектору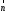 проводим прямую
проводим прямую .
.
Необходимо
получить минимум функции цели, т. е.
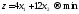 .
Параллельным переносом передвигаем
прямую
.
Параллельным переносом передвигаем
прямую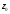 до тех пор пока весь многоугольник не
окажется сверху. В точке С пересеклись
две прямые:
до тех пор пока весь многоугольник не
окажется сверху. В точке С пересеклись
две прямые: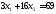 и
и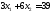 .
Следовательно, координаты точки С
находим из системы уравнений этих
прямых.
.
Следовательно, координаты точки С
находим из системы уравнений этих
прямых.
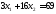 ,
,
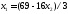 ,
,
 ;
;
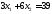 .
.
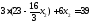
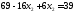
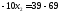
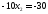
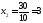
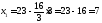
Получили С (7; 3)
Подставляя координаты точки С в уравнение функции цели, получим:
Zmin=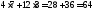 .
.
Ответ: необходимо купить 7 ед. продукта П1 и 3 ед. продукта П2, минимальные денежные затраты равны 64 ден. ед.
№ 13
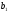 =45,
=45,
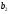 =138,
=138,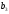 =135,
С1=13,
С2=10,
А=
=135,
С1=13,
С2=10,
А= .
.
Решение.
Данные задачи представим в таблице:
|
Питательные вещества |
Продукты |
Необходимое количество | ||
|
П1 |
П2 | |||
|
белки |
9 |
2 |
45 | |
|
жиры |
6 |
23 |
138 | |
|
углеводы |
9 |
12 |
135 | |
|
Цена |
13 |
10 |
| |
|
количество |
|
|
| |
Пусть
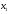 - количество единиц продукта П1,
- количество единиц продукта П1,
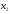 - количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
- количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
С
учетом цены за каждую единицу продукта,
покупателю необходимо будет заплатить
следующую сумму: z=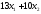 денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
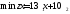
Продукты
необходимо закупить в таком количестве,
чтобы обеспечить организм необходимым
количеством питательных веществ, т. е.
переменные
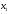 ,
, должны удовлетворять ограничениям.
должны удовлетворять ограничениям.
В
одной единице продукта П1
содержится 9 усл. ед. белка, тогда в х1
единицах содержится
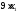 единиц белка. В одной единице продукта
П2
содержится 2 усл. ед. белка, тогда в х2
единицах содержится
единиц белка. В одной единице продукта
П2
содержится 2 усл. ед. белка, тогда в х2
единицах содержится
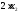 усл. ед. белка.
усл. ед. белка.
Тогда
суммарное количество усл. ед. белка в
рационе равно
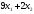 .
.
В
организме же белка должно быть не меньше
необходимого количества, т. е. не меньше
45. Получим первое ограничение
 .
.
Рассуждая
аналогично, и просматривая строку «жиры»
данной таблицы, получим второе ограничение:

Просматривая
строку «углеводы» данной таблицы,
получим третье ограничение:
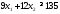
Учтем,
что переменные
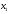 ,
,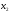 должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
Математическая модель исходной задачи имеет вид:
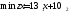
 ,
,
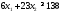 ,
,
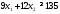 ,
,
 ,
,
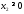 .
.
Строим в прямоугольной декартовой системе координат прямые.
1.
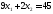 .
.
|
х1 |
5 |
3 |
|
х2 |
0 |
9 |
2.
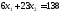 .
.
|
х1 |
0 |
11,5 |
|
х2 |
6 |
3 |
3.
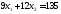 .
.
|
х1 |
15 |
5 |
|
х2 |
0 |
7,5 |
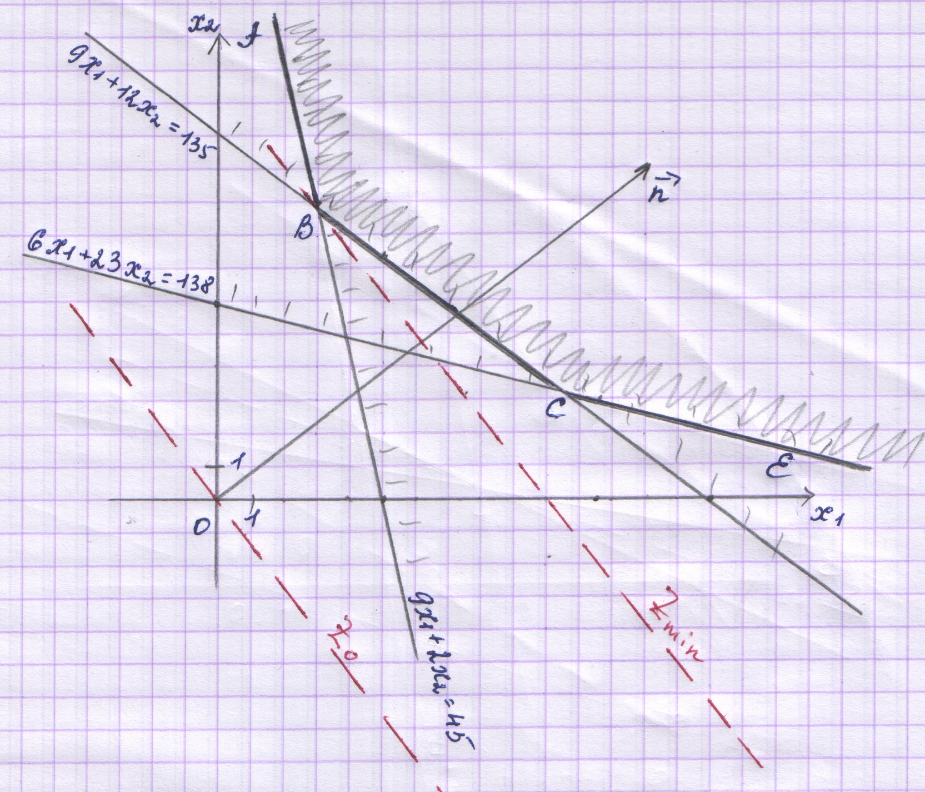
Каждая из этих прямых разбивает плоскость на две полуплоскости. Только одна из полуплоскостей является решением соответствующего неравенства. Пересечение решений трех неравенств является решением системы – многоугольником решений.
Возьмем точку (1; 1) и подставим в каждое неравенство системы.
1.
 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства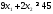 .
.
2.
 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства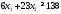 .
.
3.
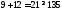 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства .
.
Учтем,
что
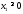 ,
,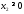 .
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
.
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
Строим
вектор
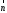 с началом в точке (0; 0) и концов в точке
(13; 10). Перпендикулярно вектору
с началом в точке (0; 0) и концов в точке
(13; 10). Перпендикулярно вектору проводим прямую
проводим прямую .
.
Необходимо
получить минимум функции цели, т. е.
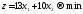 .
Параллельным переносом передвигаем
прямую
.
Параллельным переносом передвигаем
прямую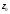 до тех пор пока весь многоугольник не
окажется сверху. В точке В пересеклись
две прямые:
до тех пор пока весь многоугольник не
окажется сверху. В точке В пересеклись
две прямые: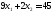 и
и .
Следовательно, координаты точки В
находим из системы уравнений этих
прямых.
.
Следовательно, координаты точки В
находим из системы уравнений этих
прямых.
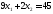 ,
,
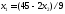 ,
,
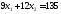 ;
;
 .
.
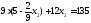
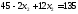
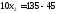

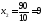
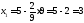
Получили В (3; 9)
Подставляя координаты точки В в уравнение функции цели, получим:
Zmin=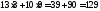 .
.
Ответ: необходимо купить 3 ед. продукта П1 и 9 ед. продукта П2, минимальные денежные затраты равны 129 ден. ед.
№ 14
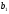 =92,
=92,
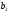 =128,
=128,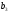 =56,
С1=12,
С2=11,
А=
=56,
С1=12,
С2=11,
А= .
.
Решение.
Данные задачи представим в таблице:
|
Питательные вещества |
Продукты |
Необходимое количество | ||
|
П1 |
П2 | |||
|
белки |
4 |
23 |
92 | |
|
жиры |
8 |
12 |
128 | |
|
углеводы |
8 |
3 |
56 | |
|
Цена |
12 |
11 |
| |
|
количество |
|
|
| |
Пусть
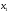 - количество единиц продукта П1,
- количество единиц продукта П1,
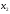 - количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
- количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
С
учетом цены за каждую единицу продукта,
покупателю необходимо будет заплатить
следующую сумму: z= денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
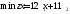
Продукты
необходимо закупить в таком количестве,
чтобы обеспечить организм необходимым
количеством питательных веществ, т. е.
переменные
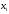 ,
, должны удовлетворять ограничениям.
должны удовлетворять ограничениям.
В
одной единице продукта П1
содержится 4 усл. ед. белка, тогда в х1
единицах содержится
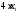 единиц белка. В одной единице продукта
П2
содержится 23 усл. ед. белка, тогда в х2
единицах содержится
единиц белка. В одной единице продукта
П2
содержится 23 усл. ед. белка, тогда в х2
единицах содержится
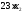 усл. ед. белка.
усл. ед. белка.
Тогда
суммарное количество усл. ед. белка в
рационе равно
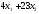 .
.
В
организме же белка должно быть не меньше
необходимого количества, т. е. не меньше
92. Получим первое ограничение
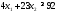 .
.
Рассуждая
аналогично, и просматривая строку «жиры»
данной таблицы, получим второе ограничение:
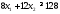
Просматривая
строку «углеводы» данной таблицы,
получим третье ограничение:
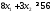
Учтем,
что переменные
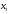 ,
, должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
Математическая модель исходной задачи имеет вид:
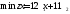
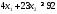 ,
,
 ,
,
 ,
,
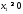 ,
,
 .
.
Строим в прямоугольной декартовой системе координат прямые.
1.
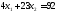 .
.
|
х1 |
0 |
11,5 |
|
х2 |
4 |
2 |
2.
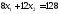 .
.
|
х1 |
1 |
16 |
|
х2 |
10 |
0 |
3.
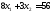 .
.
|
х1 |
4 |
7 |
|
х2 |
8 |
0 |
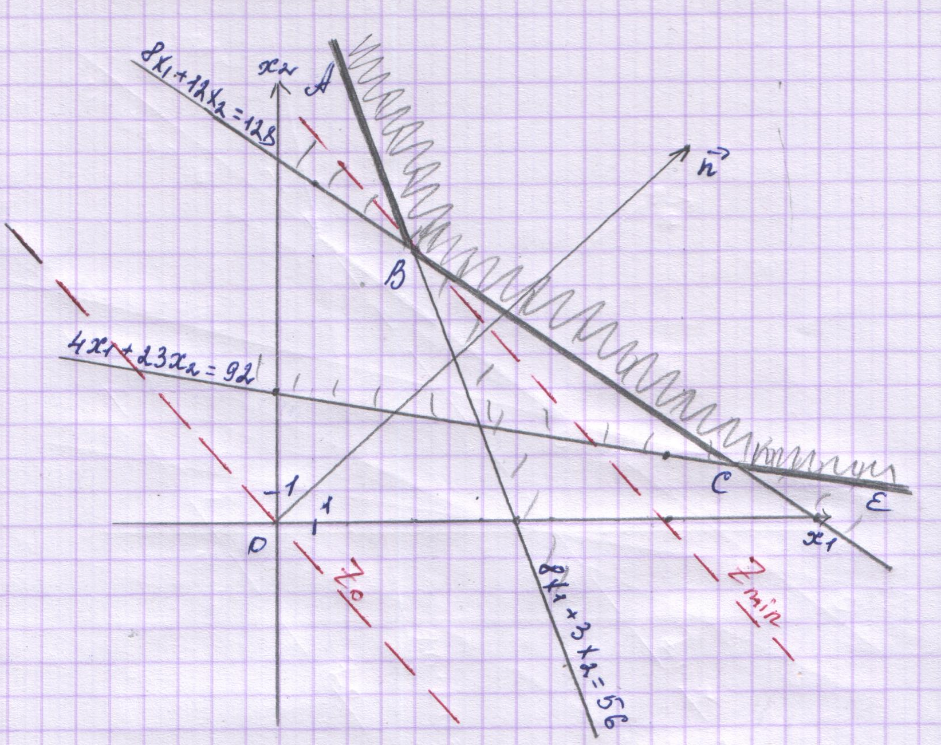
Каждая из этих прямых разбивает плоскость на две полуплоскости. Только одна из полуплоскостей является решением соответствующего неравенства. Пересечение решений трех неравенств является решением системы – многоугольником решений.
Возьмем точку (1; 1) и подставим в каждое неравенство системы.
1.
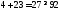 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства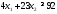 .
.
2.
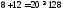 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства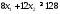 .
.
3.
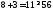 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства .
.
Учтем,
что
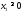 ,
, .
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
.
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
Строим
вектор
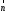 с началом в точке (0; 0) и концов в точке
(12; 11). Перпендикулярно вектору
с началом в точке (0; 0) и концов в точке
(12; 11). Перпендикулярно вектору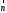 проводим прямую
проводим прямую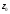 .
.
Необходимо
получить минимум функции цели, т. е.
 .
Параллельным переносом передвигаем
прямую
.
Параллельным переносом передвигаем
прямую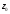 до тех пор пока весь многоугольник не
окажется сверху. В точке В пересеклись
две прямые:
до тех пор пока весь многоугольник не
окажется сверху. В точке В пересеклись
две прямые: и
и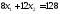 .
Следовательно, координаты точки В
находим из системы уравнений этих
прямых.
.
Следовательно, координаты точки В
находим из системы уравнений этих
прямых.
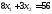 ,
,
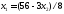 ,
,
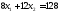 ;
;
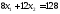 .
.
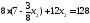
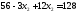
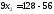

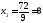
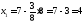
Получили В (4; 8)
Подставляя координаты точки В в уравнение функции цели, получим:
Zmin=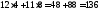 .
.
Ответ: необходимо купить 4 ед. продукта П1 и 8 ед. продукта П2, минимальные денежные затраты равны 136 ден. ед.
№ 15
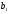 =63,
=63,
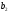 =147,
=147,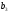 =126,
С1=12,
С2=9,
А=
=126,
С1=12,
С2=9,
А= .
.
Решение.
Данные задачи представим в таблице:
|
Питательные вещества |
Продукты |
Необходимое количество | ||
|
П1 |
П2 | |||
|
белки |
9 |
3 |
63 | |
|
жиры |
7 |
21 |
147 | |
|
углеводы |
9 |
10 |
126 | |
|
Цена |
12 |
9 |
| |
|
количество |
|
|
| |
Пусть
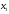 - количество единиц продукта П1,
- количество единиц продукта П1,
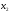 - количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
- количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
С
учетом цены за каждую единицу продукта,
покупателю необходимо будет заплатить
следующую сумму: z= денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:

Продукты
необходимо закупить в таком количестве,
чтобы обеспечить организм необходимым
количеством питательных веществ, т. е.
переменные
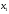 ,
,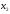 должны удовлетворять ограничениям.
должны удовлетворять ограничениям.
В
одной единице продукта П1
содержится 9 усл. ед. белка, тогда в х1
единицах содержится
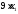 единиц белка. В одной единице продукта
П2
содержится 3 усл. ед. белка, тогда в х2
единицах содержится
единиц белка. В одной единице продукта
П2
содержится 3 усл. ед. белка, тогда в х2
единицах содержится
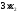 усл. ед. белка.
усл. ед. белка.
Тогда
суммарное количество усл. ед. белка в
рационе равно
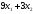 .
.
В
организме же белка должно быть не меньше
необходимого количества, т. е. не меньше
63. Получим первое ограничение
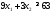 .
.
Рассуждая
аналогично, и просматривая строку «жиры»
данной таблицы, получим второе ограничение:
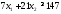
Просматривая
строку «углеводы» данной таблицы,
получим третье ограничение:
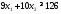
Учтем,
что переменные
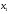 ,
,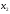 должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
Математическая модель исходной задачи имеет вид:
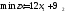
 ,
,
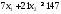 ,
,
 ,
,
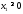 ,
,
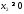 .
.
Строим в прямоугольной декартовой системе координат прямые.
1.
 .
.
|
х1 |
7 |
3 |
|
х2 |
0 |
12 |
2.
 .
.
|
х1 |
0 |
9 |
|
х2 |
7 |
4 |
3.
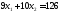 .
.
|
х1 |
14 |
4 |
|
х2 |
0 |
9 |
Каждая из этих прямых разбивает плоскость на две полуплоскости. Только одна из полуплоскостей является решением соответствующего неравенства. Пересечение решений трех неравенств является решением системы – многоугольником решений.
Возьмем точку (1; 1) и подставим в каждое неравенство системы.
1.
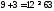 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства .
.
2.
 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства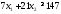 .
.
3.
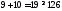 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства .
.
Учтем,
что
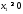 ,
,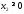 .
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
.
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
Строим
вектор
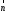 с началом в точке (0; 0) и концов в точке
(12; 9). Перпендикулярно вектору
с началом в точке (0; 0) и концов в точке
(12; 9). Перпендикулярно вектору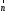 проводим прямую
проводим прямую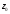 .
.
Необходимо
получить минимум функции цели, т. е.
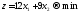 .
Параллельным переносом передвигаем
прямую
.
Параллельным переносом передвигаем
прямую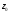 до тех пор пока весь многоугольник не
окажется сверху. В точке В пересеклись
две прямые:
до тех пор пока весь многоугольник не
окажется сверху. В точке В пересеклись
две прямые: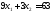 и
и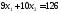 .
Следовательно, координаты точки В
находим из системы уравнений этих
прямых.
.
Следовательно, координаты точки В
находим из системы уравнений этих
прямых.
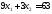 ,
,
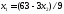 ,
,
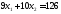 ;
;
 .
.


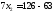
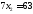
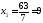
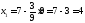
Получили В (4; 9)
Подставляя координаты точки В в уравнение функции цели, получим:
Zmin= .
.
Ответ: необходимо купить 4 ед. продукта П1 и 9 ед. продукта П2, минимальные денежные затраты равны 129 ден. ед.
№ 16
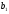 =60,
=60,
 =24,
=24,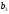 =105,
С1=3,
С2=6,
А=
=105,
С1=3,
С2=6,
А= .
.
Решение.
Данные задачи представим в таблице:
|
Питательные вещества |
Продукты |
Необходимое количество | ||
|
П1 |
П2 | |||
|
белки |
3 |
14 |
60 | |
|
жиры |
3 |
2 |
24 | |
|
углеводы |
21 |
5 |
105 | |
|
Цена |
3 |
6 |
| |
|
количество |
|
|
| |
Пусть
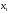 - количество единиц продукта П1,
- количество единиц продукта П1,
 - количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
- количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
С
учетом цены за каждую единицу продукта,
покупателю необходимо будет заплатить
следующую сумму: z= денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:

Продукты
необходимо закупить в таком количестве,
чтобы обеспечить организм необходимым
количеством питательных веществ, т. е.
переменные
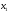 ,
,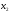 должны удовлетворять ограничениям.
должны удовлетворять ограничениям.
В
одной единице продукта П1
содержится 3 усл. ед. белка, тогда в х1
единицах содержится
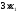 единиц белка. В одной единице продукта
П2
содержится 14 усл. ед. белка, тогда в х2
единицах содержится
единиц белка. В одной единице продукта
П2
содержится 14 усл. ед. белка, тогда в х2
единицах содержится
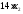 усл. ед. белка.
усл. ед. белка.
Тогда
суммарное количество усл. ед. белка в
рационе равно
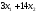 .
.
В
организме же белка должно быть не меньше
необходимого количества, т. е. не меньше
60. Получим первое ограничение
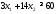 .
.
Рассуждая
аналогично, и просматривая строку «жиры»
данной таблицы, получим второе ограничение:
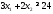
Просматривая
строку «углеводы» данной таблицы,
получим третье ограничение:
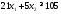
Учтем,
что переменные
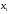 ,
,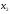 должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
Математическая модель исходной задачи имеет вид:

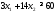 ,
,
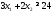 ,
,
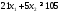 ,
,
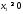 ,
,
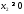 .
.
Строим в прямоугольной декартовой системе координат прямые.
1.
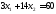 .
.
|
х1 |
6 |
13 |
|
х2 |
3 |
1,5 |
2.
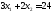 .
.
|
х1 |
0 |
8 |
|
х2 |
12 |
0 |
3.
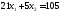 .
.
|
х1 |
2 |
5 |
|
х2 |
12,6 |
0 |
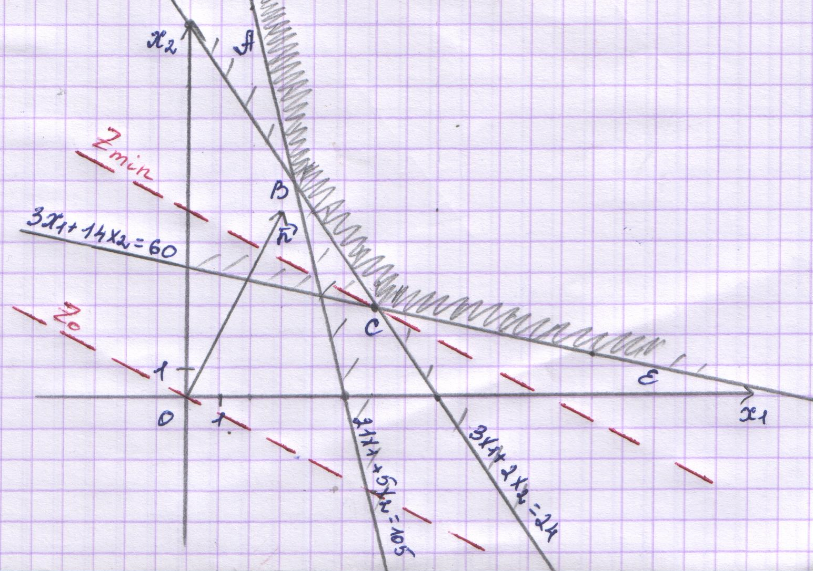
Каждая из этих прямых разбивает плоскость на две полуплоскости. Только одна из полуплоскостей является решением соответствующего неравенства. Пересечение решений трех неравенств является решением системы – многоугольником решений.
Возьмем точку (1; 1) и подставим в каждое неравенство системы.
1.
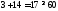 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства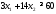 .
.
2.
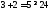 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства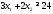 .
.
3.
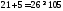 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства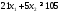 .
.
Учтем,
что
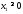 ,
,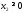 .
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
.
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
Строим
вектор
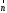 с началом в точке (0; 0) и концов в точке
(3; 6). Перпендикулярно вектору
с началом в точке (0; 0) и концов в точке
(3; 6). Перпендикулярно вектору проводим прямую
проводим прямую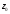 .
.
Необходимо
получить минимум функции цели, т. е.
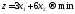 .
Параллельным переносом передвигаем
прямую
.
Параллельным переносом передвигаем
прямую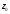 до тех пор пока весь многоугольник не
окажется сверху. В точке С пересеклись
две прямые:
до тех пор пока весь многоугольник не
окажется сверху. В точке С пересеклись
две прямые: и
и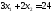 .
Следовательно, координаты точки С
находим из системы уравнений этих
прямых.
.
Следовательно, координаты точки С
находим из системы уравнений этих
прямых.
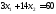 ,
,
 ,
,
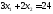 ;
;
 .
.
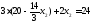
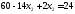
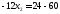
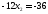
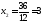
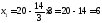
Получили С (6; 3)
Подставляя координаты точки С в уравнение функции цели, получим:
Zmin=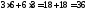 .
.
Ответ: необходимо купить 6 ед. продукта П1 и 3 ед. продукта П2, минимальные денежные затраты равны 36 ден. ед.
№ 17
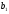 =22,
=22,
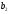 =40,
=40,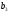 =138,
С1=4,
С2=9,
А=
=138,
С1=4,
С2=9,
А= .
.
Решение.
Данные задачи представим в таблице:
|
Питательные вещества |
Продукты |
Необходимое количество | ||
|
П1 |
П2 | |||
|
белки |
2 |
3 |
22 | |
|
жиры |
2 |
12 |
40 | |
|
углеводы |
23 |
6 |
138 | |
|
Цена |
4 |
9 |
| |
|
количество |
|
|
| |
Пусть
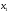 - количество единиц продукта П1,
- количество единиц продукта П1,
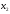 - количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
- количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
С
учетом цены за каждую единицу продукта,
покупателю необходимо будет заплатить
следующую сумму: z=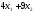 денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
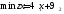
Продукты
необходимо закупить в таком количестве,
чтобы обеспечить организм необходимым
количеством питательных веществ, т. е.
переменные
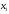 ,
, должны удовлетворять ограничениям.
должны удовлетворять ограничениям.
В
одной единице продукта П1
содержится 2 усл. ед. белка, тогда в х1
единицах содержится
 единиц белка. В одной единице продукта
П2
содержится 3 усл. ед. белка, тогда в х2
единицах содержится
единиц белка. В одной единице продукта
П2
содержится 3 усл. ед. белка, тогда в х2
единицах содержится
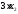 усл. ед. белка.
усл. ед. белка.
Тогда
суммарное количество усл. ед. белка в
рационе равно
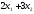 .
.
В
организме же белка должно быть не меньше
необходимого количества, т. е. не меньше
22. Получим первое ограничение
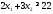 .
.
Рассуждая
аналогично, и просматривая строку «жиры»
данной таблицы, получим второе ограничение:
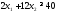
Просматривая
строку «углеводы» данной таблицы,
получим третье ограничение:
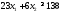
Учтем,
что переменные
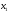 ,
,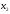 должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
Математическая модель исходной задачи имеет вид:
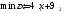
 ,
,
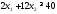 ,
,
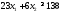 ,
,
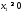 ,
,
 .
.
Строим в прямоугольной декартовой системе координат прямые.
1.
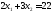 .
.
|
х1 |
11 |
8 |
|
х2 |
0 |
2 |
2.
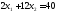 .
.
|
х1 |
2 |
8 |
|
х2 |
3 |
2 |
3.
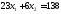 .
.
|
х1 |
6 |
3 |
|
х2 |
0 |
11,5 |
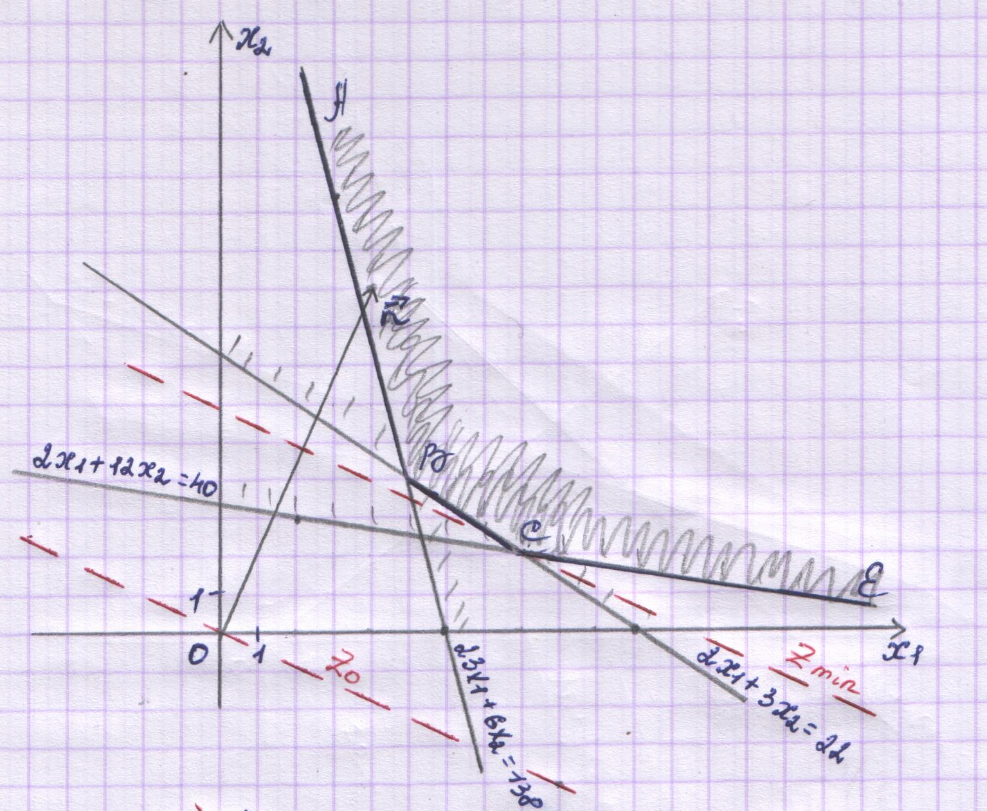
Каждая из этих прямых разбивает плоскость на две полуплоскости. Только одна из полуплоскостей является решением соответствующего неравенства. Пересечение решений трех неравенств является решением системы – многоугольником решений.
Возьмем точку (1; 1) и подставим в каждое неравенство системы.
1.
 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства .
.
2.
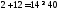 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства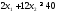 .
.
3.
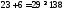 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства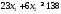 .
.
Учтем,
что
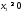 ,
,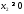 .
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
.
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
Строим
вектор
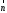 с началом в точке (0; 0) и концов в точке
(3; 6). Перпендикулярно вектору
с началом в точке (0; 0) и концов в точке
(3; 6). Перпендикулярно вектору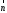 проводим прямую
проводим прямую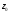 .
.
Необходимо
получить минимум функции цели, т. е.
 .
Параллельным переносом передвигаем
прямую
.
Параллельным переносом передвигаем
прямую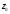 до тех пор пока весь многоугольник не
окажется сверху. В точке С пересеклись
две прямые:
до тех пор пока весь многоугольник не
окажется сверху. В точке С пересеклись
две прямые: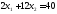 и
и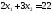 .
Следовательно, координаты точки С
находим из системы уравнений этих
прямых.
.
Следовательно, координаты точки С
находим из системы уравнений этих
прямых.
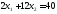 ,
,
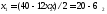 ,
,
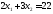 ;
;
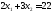 .
.
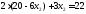
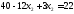
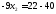
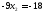
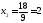
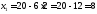
Получили С (8; 2)
Подставляя координаты точки С в уравнение функции цели, получим:
Zmin=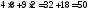 .
.
Ответ: необходимо купить 8 ед. продукта П1 и 2 ед. продукта П2, минимальные денежные затраты равны 50 ден. ед.
№ 18
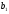 =50,
=50,
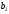 =140,
=140,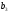 =20,
С1=4,
С2=3,
А=
=20,
С1=4,
С2=3,
А= .
.
Решение.
Данные задачи представим в таблице:
|
Питательные вещества |
Продукты |
Необходимое количество | ||
|
П1 |
П2 | |||
|
белки |
10 |
3 |
50 | |
|
жиры |
10 |
12 |
140 | |
|
углеводы |
1 |
4 |
20 | |
|
Цена |
4 |
3 |
| |
|
количество |
|
|
| |
Пусть
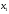 - количество единиц продукта П1,
- количество единиц продукта П1,
 - количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
- количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
С
учетом цены за каждую единицу продукта,
покупателю необходимо будет заплатить
следующую сумму: z=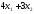 денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
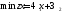
Продукты
необходимо закупить в таком количестве,
чтобы обеспечить организм необходимым
количеством питательных веществ, т. е.
переменные
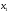 ,
,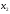 должны удовлетворять ограничениям.
должны удовлетворять ограничениям.
В
одной единице продукта П1
содержится 10 усл. ед. белка, тогда в х1
единицах содержится
 единиц белка. В одной единице продукта
П2
содержится 3 усл. ед. белка, тогда в х2
единицах содержится
единиц белка. В одной единице продукта
П2
содержится 3 усл. ед. белка, тогда в х2
единицах содержится
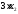 усл. ед. белка.
усл. ед. белка.
Тогда
суммарное количество усл. ед. белка в
рационе равно
 .
.
В
организме же белка должно быть не меньше
необходимого количества, т. е. не меньше
50. Получим первое ограничение
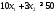 .
.
Рассуждая
аналогично, и просматривая строку «жиры»
данной таблицы, получим второе ограничение:
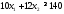
Просматривая
строку «углеводы» данной таблицы,
получим третье ограничение:
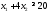
Учтем,
что переменные
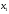 ,
,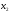 должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
Математическая модель исходной задачи имеет вид:
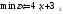
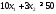 ,
,
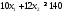 ,
,
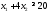 ,
,
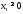 ,
,
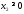 .
.
Строим в прямоугольной декартовой системе координат прямые.
1.
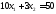 .
.
|
х1 |
5 |
2 |
|
х2 |
0 |
10 |
2.
 .
.
|
х1 |
14 |
2 |
|
х2 |
0 |
10 |
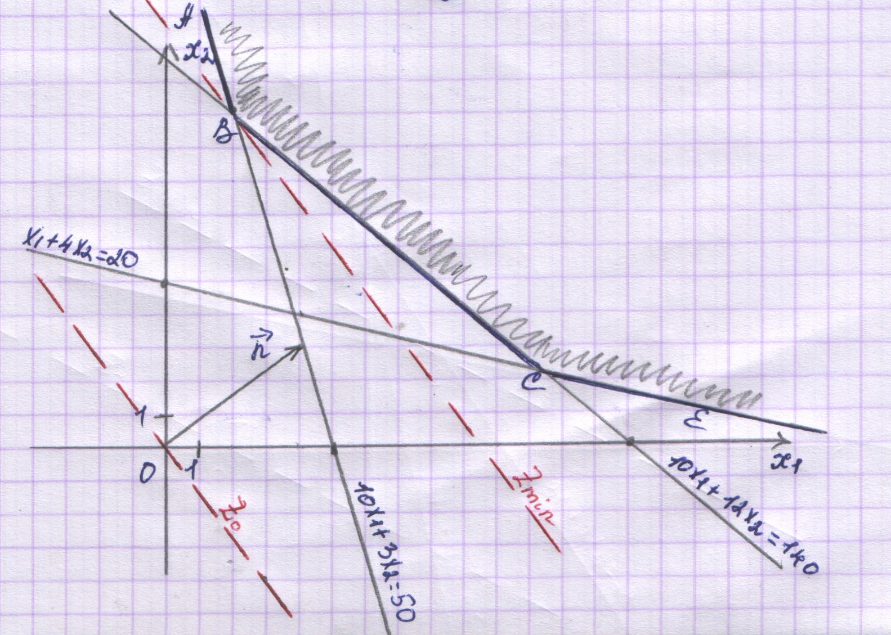
3.
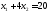 .
.
|
х1 |
0 |
4 |
|
х2 |
5 |
4 |
Каждая из этих прямых разбивает плоскость на две полуплоскости. Только одна из полуплоскостей является решением соответствующего неравенства. Пересечение решений трех неравенств является решением системы – многоугольником решений.
Возьмем точку (1; 1) и подставим в каждое неравенство системы.
1.
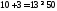 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства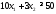 .
.
2.
 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства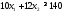 .
.
3.
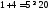 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства .
.
Учтем,
что
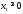 ,
,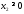 .
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
.
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
Строим
вектор
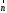 с началом в точке (0; 0) и концов в точке
(4; 3). Перпендикулярно вектору
с началом в точке (0; 0) и концов в точке
(4; 3). Перпендикулярно вектору проводим прямую
проводим прямую .
.
Необходимо
получить минимум функции цели, т. е.
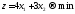 .
Параллельным переносом передвигаем
прямую
.
Параллельным переносом передвигаем
прямую до тех пор пока весь многоугольник не
окажется сверху. В точке В пересеклись
две прямые:
до тех пор пока весь многоугольник не
окажется сверху. В точке В пересеклись
две прямые: и
и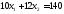 .
Следовательно, координаты точки В
находим из системы уравнений этих
прямых.
.
Следовательно, координаты точки В
находим из системы уравнений этих
прямых.
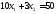 ,
,
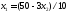 ,
,
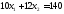 ;
;
 .
.
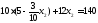

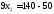
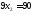
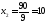
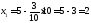
Получили В (2; 10)
Подставляя координаты точки В в уравнение функции цели, получим:
Zmin=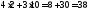 .
.
Ответ: необходимо купить 2 ед. продукта П1 и 10 ед. продукта П2, минимальные денежные затраты равны 38 ден. ед.
№ 19
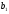 =40,
=40,
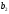 =104,
=104,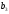 =20,
С1=7,
С2=5,
А=
=20,
С1=7,
С2=5,
А= .
.
Решение.
Данные задачи представим в таблице:
|
Питательные вещества |
Продукты |
Необходимое количество | ||
|
П1 |
П2 | |||
|
белки |
8 |
2 |
40 | |
|
жиры |
8 |
10 |
104 | |
|
углеводы |
1 |
4 |
20 | |
|
Цена |
7 |
5 |
| |
|
количество |
|
|
| |
Пусть
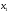 - количество единиц продукта П1,
- количество единиц продукта П1,
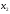 - количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
- количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
С
учетом цены за каждую единицу продукта,
покупателю необходимо будет заплатить
следующую сумму: z=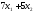 денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
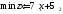
Продукты
необходимо закупить в таком количестве,
чтобы обеспечить организм необходимым
количеством питательных веществ, т. е.
переменные
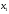 ,
,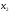 должны удовлетворять ограничениям.
должны удовлетворять ограничениям.
В
одной единице продукта П1
содержится 8 усл. ед. белка, тогда в х1
единицах содержится
 единиц белка. В одной единице продукта
П2
содержится 2 усл. ед. белка, тогда в х2
единицах содержится
единиц белка. В одной единице продукта
П2
содержится 2 усл. ед. белка, тогда в х2
единицах содержится
 усл. ед. белка.
усл. ед. белка.
Тогда
суммарное количество усл. ед. белка в
рационе равно
 .
.
В
организме же белка должно быть не меньше
необходимого количества, т. е. не меньше
40. Получим первое ограничение
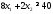 .
.
Рассуждая
аналогично, и просматривая строку «жиры»
данной таблицы, получим второе ограничение:
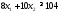
Просматривая
строку «углеводы» данной таблицы,
получим третье ограничение:
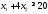
Учтем,
что переменные
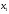 ,
,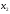 должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
Математическая модель исходной задачи имеет вид:
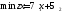
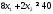 ,
,
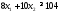 ,
,
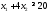 ,
,
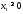 ,
,
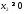 .
.
Строим в прямоугольной декартовой системе координат прямые.
1.
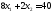 .
.
|
х1 |
5 |
3 |
|
х2 |
0 |
8 |
2.
 .
.
|
х1 |
13 |
3 |
|
х2 |
0 |
8 |
3.
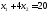 .
.
|
х1 |
0 |
4 |
|
х2 |
5 |
4 |
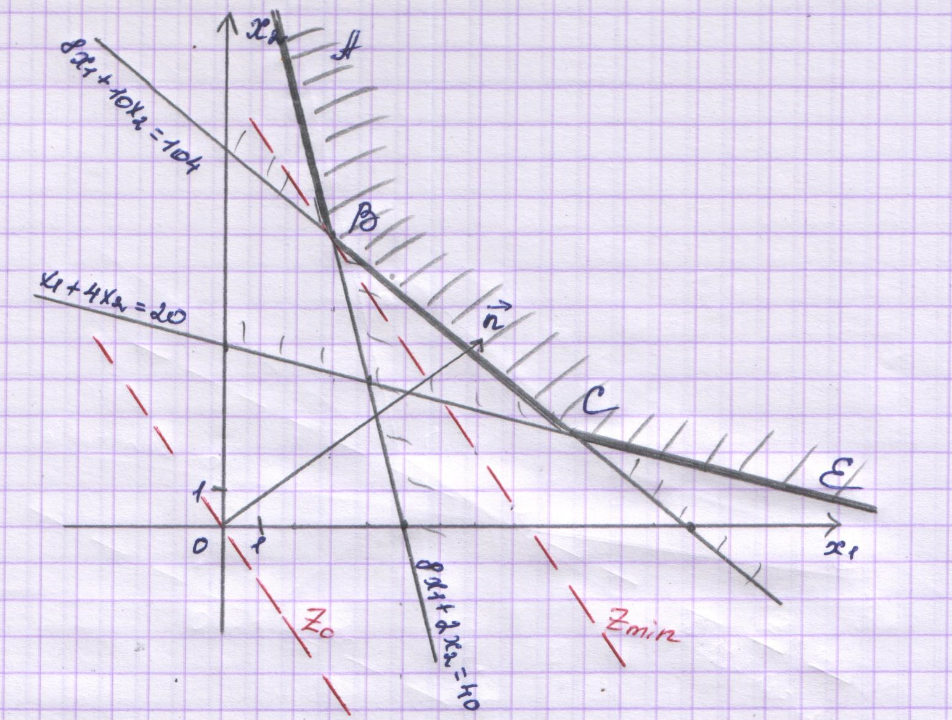
Каждая из этих прямых разбивает плоскость на две полуплоскости. Только одна из полуплоскостей является решением соответствующего неравенства. Пересечение решений трех неравенств является решением системы – многоугольником решений.
Возьмем точку (1; 1) и подставим в каждое неравенство системы.
1.
 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства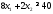 .
.
2.
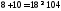 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства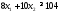 .
.
3.
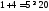 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства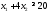 .
.
Учтем,
что
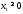 ,
, .
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
.
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
Строим
вектор
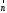 с началом в точке (0; 0) и концов в точке
(7; 5). Перпендикулярно вектору
с началом в точке (0; 0) и концов в точке
(7; 5). Перпендикулярно вектору проводим прямую
проводим прямую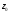 .
.
Необходимо
получить минимум функции цели, т. е.
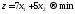 .
Параллельным переносом передвигаем
прямую
.
Параллельным переносом передвигаем
прямую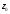 до тех пор пока весь многоугольник не
окажется сверху. В точке В пересеклись
две прямые:
до тех пор пока весь многоугольник не
окажется сверху. В точке В пересеклись
две прямые: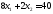 и
и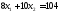 .
Следовательно, координаты точки В
находим из системы уравнений этих
прямых.
.
Следовательно, координаты точки В
находим из системы уравнений этих
прямых.
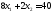 ,
,
 ,
,
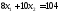 ;
;
 .
.
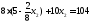
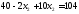
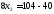

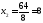
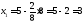
Получили В (3; 8)
Подставляя координаты точки В в уравнение функции цели, получим:
Zmin= .
.
Ответ: необходимо купить 3 ед. продукта П1 и 8 ед. продукта П2, минимальные денежные затраты равны 61 ден. ед.
№ 20
 =138,
=138,
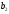 =60,
=60,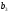 =110,
С1=6,
С2=10,
А=
=110,
С1=6,
С2=10,
А= .
.
Решение.
Данные задачи представим в таблице:
|
Питательные вещества |
Продукты |
Необходимое количество | ||
|
П1 |
П2 | |||
|
белки |
23 |
6 |
138 | |
|
жиры |
5 |
4 |
60 | |
|
углеводы |
5 |
14 |
110 | |
|
Цена |
6 |
10 |
| |
|
количество |
|
|
| |
Пусть
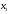 - количество единиц продукта П1,
- количество единиц продукта П1,
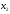 - количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
- количество единиц продукта П2,
которое планируется закупить. Таблица
дополнена этими переменными.
С
учетом цены за каждую единицу продукта,
покупателю необходимо будет заплатить
следующую сумму: z= денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
денежных единиц. Т. о. целевая функцияz(x)
будет выражать стоимость рациона,
которую необходимо минимизировать:
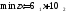
Продукты
необходимо закупить в таком количестве,
чтобы обеспечить организм необходимым
количеством питательных веществ, т. е.
переменные
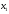 ,
,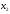 должны удовлетворять ограничениям.
должны удовлетворять ограничениям.
В
одной единице продукта П1
содержится 23 усл. ед. белка, тогда в х1
единицах содержится
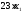 единиц белка. В одной единице продукта
П2
содержится 6 усл. ед. белка, тогда в х2
единицах содержится
единиц белка. В одной единице продукта
П2
содержится 6 усл. ед. белка, тогда в х2
единицах содержится
 усл. ед. белка.
усл. ед. белка.
Тогда
суммарное количество усл. ед. белка в
рационе равно
 .
.
В
организме же белка должно быть не меньше
необходимого количества, т. е. не меньше
138. Получим первое ограничение
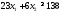 .
.
Рассуждая
аналогично, и просматривая строку «жиры»
данной таблицы, получим второе ограничение:
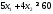
Просматривая
строку «углеводы» данной таблицы,
получим третье ограничение:
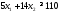
Учтем,
что переменные
 ,
,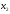 должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
должны быть неотрицательными (нельзя
купить отрицательное число единиц
продукта).
Математическая модель исходной задачи имеет вид:
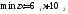
 ,
,
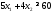 ,
,
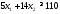 ,
,
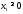 ,
,
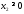 .
.
Строим в прямоугольной декартовой системе координат прямые.
1.
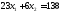 .
.
|
х1 |
6 |
3 |
|
х2 |
0 |
11,5 |
2.
 .
.
|
х1 |
12 |
4 |
|
х2 |
0 |
10 |
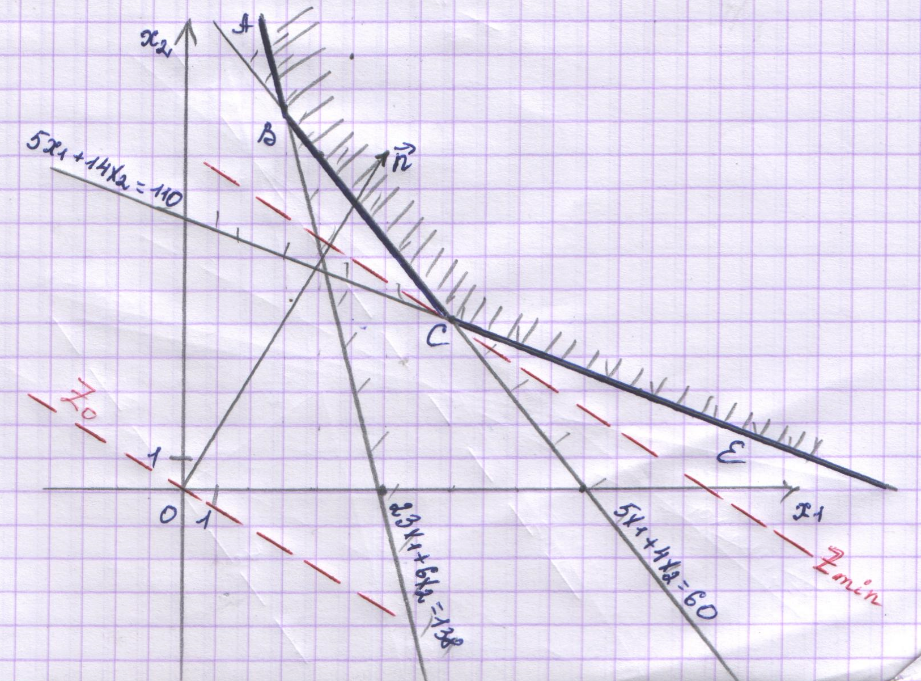
3.
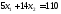 .
.
|
х1 |
8 |
13,6 |
|
х2 |
5 |
3 |
Каждая из этих прямых разбивает плоскость на две полуплоскости. Только одна из полуплоскостей является решением соответствующего неравенства. Пересечение решений трех неравенств является решением системы – многоугольником решений.
Возьмем точку (1; 1) и подставим в каждое неравенство системы.
1.
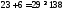 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства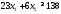 .
.
2.
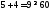 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства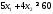 .
.
3.
 не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства
не верно. Часть плоскости, в которой
лежит точка (1; 1) не является решением
неравенства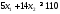 .
.
Учтем,
что
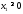 ,
, .
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
.
Заштриховав соответствующие области,
получим многоугольник решений АВСЕ –
неограничен сверху.
Строим
вектор
 с началом в точке (0; 0) и концов в точке
(6; 10). Перпендикулярно вектору
с началом в точке (0; 0) и концов в точке
(6; 10). Перпендикулярно вектору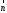 проводим прямую
проводим прямую .
.
Необходимо
получить минимум функции цели, т. е.
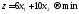 .
Параллельным переносом передвигаем
прямую
.
Параллельным переносом передвигаем
прямую до тех пор пока весь многоугольник не
окажется сверху. В точке С пересеклись
две прямые:
до тех пор пока весь многоугольник не
окажется сверху. В точке С пересеклись
две прямые: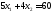 и
и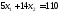 .
Следовательно, координаты точки С
находим из системы уравнений этих
прямых.
.
Следовательно, координаты точки С
находим из системы уравнений этих
прямых.
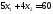 ,
,
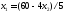 ,
,
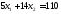 ;
;
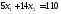 .
.
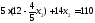
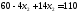
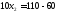
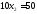
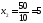
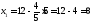
Получили С (8; 5)
Подставляя координаты точки С в уравнение функции цели, получим:
Zmin=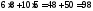 .
.
Ответ: необходимо купить 8 ед. продукта П1 и 5 ед. продукта П2, минимальные денежные затраты равны 98 ден. ед.