
- •Менський Микола Іванович побудова фрактальних зображень
- •Основна частина Що таке фрактал ?
- •Множина Мандельброта
- •Фрактальні орбіти
- •Ітераційні функціональні системи (ifs)
- •Геометричні фрактали.
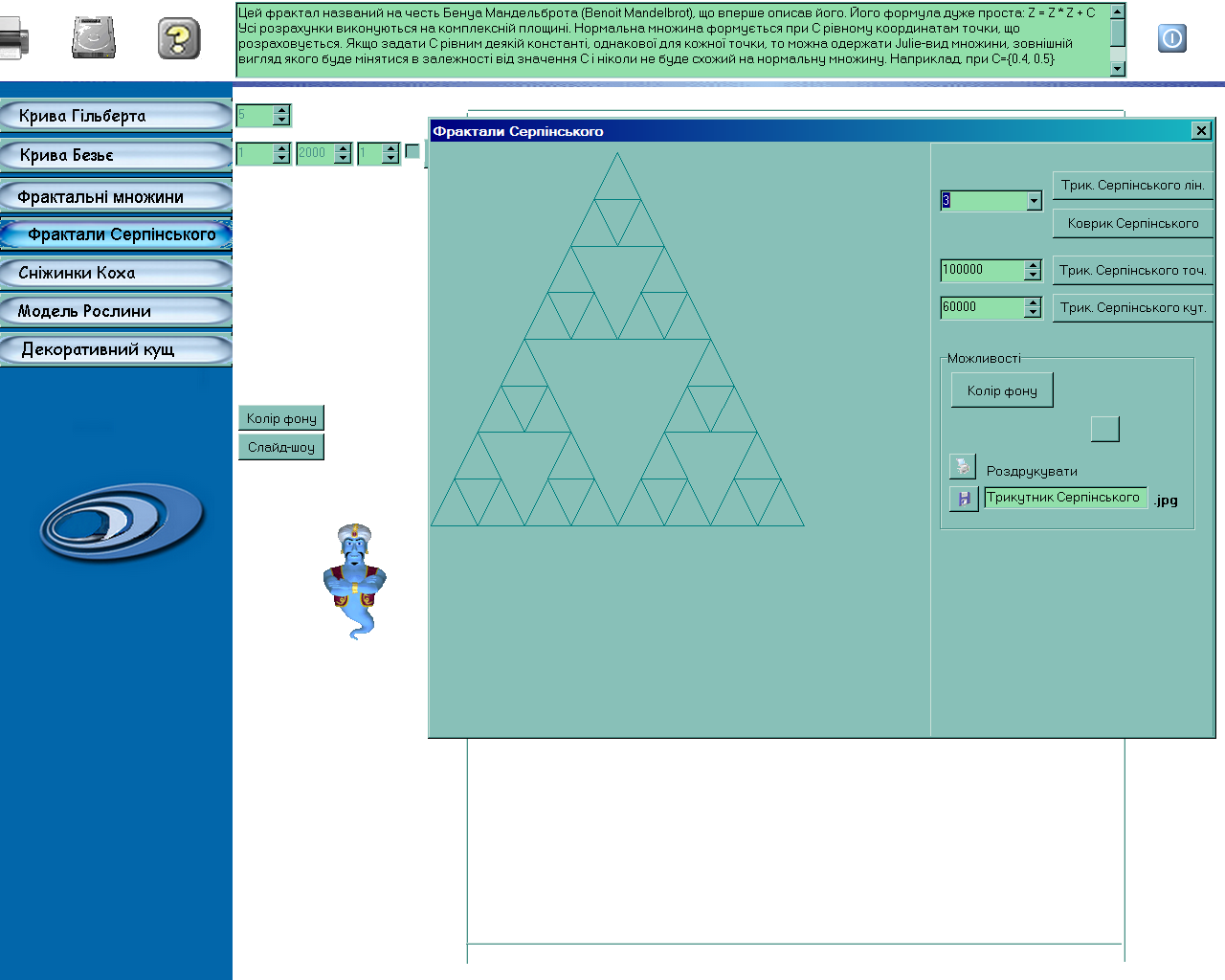
- •Побудова графічного зображення трикутника Серпінського
- •Побудова графічного зображення кривої Коха
- •Крива Гільберта
- •Крива Безьє
- •Технічне завдання Опис схеми програмного продукту «Фрактальний сад»
- •Вимоги до програмного забезпечення
- •Вимоги до апаратного забезпечення
- •Стадії та етапи розробки
- •Опис застосування
- •Висновок
- •Рекомендації
- •Список використаної літератури:
- •Додатки
- •Построение фракталов. Часть первая.
Рекомендації
Простіше кажучи, комп’ютерна графіка - це те що ми бачимо на моніторі комп’ютера, це те, що діє на наші органи зору, те, що разом із суто інформаційною складовою несе емоційне навантаження.
На мою думку вивчення шкільного курсу комп’ютерної графіки повинно бути більш глибоким та ефективним.
Можливо тему «Графічні операції» в програмуванні слід вивчати відразу після лінійних алгоритмів і тоді вивчення розгалужень і циклів можна буде наповнити новим змістом - графічними елементами.
Використовувати програмний продукт «Фрактальний сад» можна на початку вивчення програмування, це дає хороший мотиваційний поштовх до створення власних програм, унаочнює поняття інформаційної моделі. Підтвердилась ефективність використання посібника та програмного продукту на уроках створення графічних програм.
У перспективі – розробка нової версії посібника та програмного продукту з підтримкою побудови об’ємних фрактальних зображень
Вивчення курсу інформатики в загальноосвітній школі повинно бути не тільки змістовно, але й емоційно наповненим. Учні, що володіють навичками роботи на комп’ютері, знають основи програмування – «золотий запас» нації, її інтелектуальна еліта. Необхідно зробити все, щоб у їх знаннях не було прогалин, а їх компетенції були повними і цілісними
Список використаної літератури:
Глинський Я.М. Turbo Pascal & Delphi 2002.
Васильев П.П. Turbo Pascal – мой друг: М.: Компьютер, ЮНИТИ, 1995.-96с.
Анохін В.Є. Язык программирования Delphi 7 2000.
Програмирование в Turbo Pascal и Delphi, 1999.
Додатки

















Построение фракталов. Часть первая.
Хочу
поделиться одним интересным способом
раскраски холста, называемым
фракталом.
Всего мною лично было
опробовано 3 способа реализации фракталов,
но все они происходили посредством
написания рекурсивной процедуры. Сам
смысл рекурсивной (в математике —
рекуррентной) процедуры в том, что она
вызывает сама себя внутри своего тела.
Вызов происходит обычным образом, как
если бы мы это делали в основном теле
программы.
Смысл первого способа
заключается в том, что мы производим
все вычисления в памяти самой рекурсии,
самой программы. Это самый банальный и
легко реализуемый способ, но и как
водится в нашем мире — самый дорогостоящий…
в плане затрат ресурсов.
Прежде всего
необходимо определиться — что мы хотим
нарисовать — будь то банальный узор,
возможно снежинка Коха — или что-то
интересное с математической точки
зрения — как например фрактал Бенуа
Мандельброта: выбор исключительно за
вами. Давайте определимся, что я буду
сторить для примера небольшое фрактальное
симметричное деревце.
![]() Принцип
его построения в последовательной
надстройке: сначала мы сторим основание,
на нём на длине 1/3 от «корня» Расположены
две первые ветки под углом Pi/6, и на 2/3
две другие, чуть поменьше. Далее мы
принимаем каждую из веток как
самостоятельное деревце, корнем которого
будет являться собственно ветка. Таким
образом получим вторую итерацию:
Принцип
его построения в последовательной
надстройке: сначала мы сторим основание,
на нём на длине 1/3 от «корня» Расположены
две первые ветки под углом Pi/6, и на 2/3
две другие, чуть поменьше. Далее мы
принимаем каждую из веток как
самостоятельное деревце, корнем которого
будет являться собственно ветка. Таким
образом получим вторую итерацию: Дальнейшей
преобразования должны быть ясны.
Начнём
реализацию с простого — разместим на
форме компоненты TImage, TEdit и TButton. Первый
будет служить полотном для рисования,
второй для принятия уровня рисуемого
фрактала, и третий соответственно для
запуска. Хочу заметить, что вывод будет
осуществляться стандартными средствами,
т.к. главное понять суть, а техническая
часть может быть улучшена
самостоятельно.
Создаём нашу рекурсивную
процедуру, в параметрах мы должны
передать ей координаты
{x,y} (я
выбрал координаты «корня», но вы можете
условиться для себя на другие — всё
равно расчёты относительны), длину
{Lh}(необходимо
для аккуратного уменьшения), угол{angle},
т.е. в каком направлении строить
и уровень{level} самой
рекурсии — для контроля её
окончания.
(1)Координаты.
Всё в этом мире зависит от пространственных
координат. Поэтому и наша плоскость
рисования не является исключением. x,y
– это координаты точки, от которой мы
будем вести наши дальнейшие расчёты.
Но это сложно осуществить без следующих
2-х параметров:
(2)Длина.
Фактически, это длина ветки. Она будет
помогать определять смещение
координат.
(3)Угол.
После вышеизложенного материала у
читателя с пытливым умом уже должен был
возникнуть вопрос о том, как вести не
абсолютное, но относительное
позиционирование. Ответ прост: мы
воспользуемся школьной теорией. Ведь
для того чтобы определить положение
точки через длину конечного отрезка
достаточно знать угол, косинус или синус
коего будет умножаться на длину.
(4)Уровень.
Для того чтобы контролировать нашу
процедуру — а она в нашем случае как
ядерная реакция, её продукт является
топливом для следующего уровня. Делается
это просто. В самом начале мы ставим
разветвитель — условие, которое будет
проверять переменную уровня итерации
и сравнивать её скажем с 1(level>1).Далее
имеем, если да, то необходимо вызвать
эту же процедуру но с параметрами,
указывающими координаты начала веток
в виде параметров «корня», угол у нас
будет поворачиваться на -Pi/6 и +
Pi/6(angle-Pi/6 и angle+Pi/6). {Примечание} {Существует
небольшой вариант, при котором вы будете
продолжать рисовать ветки не только на
самих ветках, но и на самом первом
основании, тобишь по стволу будут также
расходиться маленькие ветки наряду с
большими, образующими опоры. В этом
случае надо будет написать отдельный
вариант на тот же угол angle что и наш, без
отклонения.} Длину Lh уменьшим соответствующим
образом, т.е. если скажем длина основного
ствола была h, а ветка получилась длины
h/2, то в параметрах передадим h/2. Ну и
наконец уровень level. Его необходимо
уменьшить на 1. Таким образом нам надо
вызвать процедуру 4{5,6} раза.
Сразу
после тела цикла должны быть процедуры
рисования — они выполняются при
невыполнении условия {чаще всего при
level=1, но бывали и другие случаи}. Тут
рисуем задуманные объекты в виде процедур
рисования. В Delphi это выглядит примерно
так:
With
Image1.Canvas do
begin
MoveTo(x,y); //Перейти
к точке "Корня"
LineTo(X+3*Lh*cos(angle),
y+3*Lh*sin(angle)) //Линия
к точке, получаемая как точка радиуса
3*Lh под углом angle. При этом Lh здесь не как
вся длина ствола дабы упростить расчёты
веток - иначе придется округлять
результаты деления длины на
3.
MoveTo(x+Lh*Cos(angle),y+lh*sin(angle));
LineTo(x+Lh*(Cos(angle)+cos(angle-Pi/6)/2),y+lh*(sin(angle)+sin(angle-Pi/6)/2)); //Первая
ветка
влево
MoveTo(x+Lh*Cos(angle),y+lh*sin(angle));
LineTo(x+Lh*(Cos(angle)+cos(angle-Pi/6)/2),y+lh*(sin(angle)+sin(angle-Pi/6)/2)); //Первая
ветка
вправо
MoveTo(x+2*Lh*cos(angle),y+2*Lh*sin(angle));
LineTo(x+Lh*(2*Cos(angle)+cos(angle-Pi/6)/3),y+lh*(2*sin(angle)+sin(angle-Pi/6)/3)); //Вторая
ветка
влево
MoveTo(x+2*Lh*cos(angle),y+2*Lh*sin(angle));
LineTo(x+Lh*(2*Cos(angle)+cos(angle+Pi/6)/3),y+lh*(2*sin(angle)+sin(angle+Pi/6)/3)); //Вторая
ветка вправо
end;
После
всего сделанного остаётся только
написать обработчик события нажатия
клавиши, в котором вызвать первый раз
процедуру с приблизительно следующими
параметрами: координаты – середина
формы по x и её низ по y; Длина – чуть
меньше высоты формы делённая на 3; угол
– вертикально вверх {в Delphi это будет
–Pi/2}; А уровень достаточно считать из
TEdit.
В конце лишь хочу заметить тот
факт, что работа будет происходить
медленно на уровнях выше 9, т.к. вся работа
происходит параллельно: высчитывание
координат по формулам для чисел с
плавающей точкой, обращение к секторам
винчестера, да и собственно сам процесс
рисования на полотне – всё это очень
трудоёмко, когда речь идёт о 9 уровне
вложенности процедуры самой в себя. {4
в степени (9-1) + 1 = 65'537 — количество
вызванных нами процедур. Для понимающего
человека это исчерпывающее объяснение.}
Поэтому при следующей нашей встрече я
опишу иной, более последовательный
способ обработки информации.
Дальнейшей
преобразования должны быть ясны.
Начнём
реализацию с простого — разместим на
форме компоненты TImage, TEdit и TButton. Первый
будет служить полотном для рисования,
второй для принятия уровня рисуемого
фрактала, и третий соответственно для
запуска. Хочу заметить, что вывод будет
осуществляться стандартными средствами,
т.к. главное понять суть, а техническая
часть может быть улучшена
самостоятельно.
Создаём нашу рекурсивную
процедуру, в параметрах мы должны
передать ей координаты
{x,y} (я
выбрал координаты «корня», но вы можете
условиться для себя на другие — всё
равно расчёты относительны), длину
{Lh}(необходимо
для аккуратного уменьшения), угол{angle},
т.е. в каком направлении строить
и уровень{level} самой
рекурсии — для контроля её
окончания.
(1)Координаты.
Всё в этом мире зависит от пространственных
координат. Поэтому и наша плоскость
рисования не является исключением. x,y
– это координаты точки, от которой мы
будем вести наши дальнейшие расчёты.
Но это сложно осуществить без следующих
2-х параметров:
(2)Длина.
Фактически, это длина ветки. Она будет
помогать определять смещение
координат.
(3)Угол.
После вышеизложенного материала у
читателя с пытливым умом уже должен был
возникнуть вопрос о том, как вести не
абсолютное, но относительное
позиционирование. Ответ прост: мы
воспользуемся школьной теорией. Ведь
для того чтобы определить положение
точки через длину конечного отрезка
достаточно знать угол, косинус или синус
коего будет умножаться на длину.
(4)Уровень.
Для того чтобы контролировать нашу
процедуру — а она в нашем случае как
ядерная реакция, её продукт является
топливом для следующего уровня. Делается
это просто. В самом начале мы ставим
разветвитель — условие, которое будет
проверять переменную уровня итерации
и сравнивать её скажем с 1(level>1).Далее
имеем, если да, то необходимо вызвать
эту же процедуру но с параметрами,
указывающими координаты начала веток
в виде параметров «корня», угол у нас
будет поворачиваться на -Pi/6 и +
Pi/6(angle-Pi/6 и angle+Pi/6). {Примечание} {Существует
небольшой вариант, при котором вы будете
продолжать рисовать ветки не только на
самих ветках, но и на самом первом
основании, тобишь по стволу будут также
расходиться маленькие ветки наряду с
большими, образующими опоры. В этом
случае надо будет написать отдельный
вариант на тот же угол angle что и наш, без
отклонения.} Длину Lh уменьшим соответствующим
образом, т.е. если скажем длина основного
ствола была h, а ветка получилась длины
h/2, то в параметрах передадим h/2. Ну и
наконец уровень level. Его необходимо
уменьшить на 1. Таким образом нам надо
вызвать процедуру 4{5,6} раза.
Сразу
после тела цикла должны быть процедуры
рисования — они выполняются при
невыполнении условия {чаще всего при
level=1, но бывали и другие случаи}. Тут
рисуем задуманные объекты в виде процедур
рисования. В Delphi это выглядит примерно
так:
With
Image1.Canvas do
begin
MoveTo(x,y); //Перейти
к точке "Корня"
LineTo(X+3*Lh*cos(angle),
y+3*Lh*sin(angle)) //Линия
к точке, получаемая как точка радиуса
3*Lh под углом angle. При этом Lh здесь не как
вся длина ствола дабы упростить расчёты
веток - иначе придется округлять
результаты деления длины на
3.
MoveTo(x+Lh*Cos(angle),y+lh*sin(angle));
LineTo(x+Lh*(Cos(angle)+cos(angle-Pi/6)/2),y+lh*(sin(angle)+sin(angle-Pi/6)/2)); //Первая
ветка
влево
MoveTo(x+Lh*Cos(angle),y+lh*sin(angle));
LineTo(x+Lh*(Cos(angle)+cos(angle-Pi/6)/2),y+lh*(sin(angle)+sin(angle-Pi/6)/2)); //Первая
ветка
вправо
MoveTo(x+2*Lh*cos(angle),y+2*Lh*sin(angle));
LineTo(x+Lh*(2*Cos(angle)+cos(angle-Pi/6)/3),y+lh*(2*sin(angle)+sin(angle-Pi/6)/3)); //Вторая
ветка
влево
MoveTo(x+2*Lh*cos(angle),y+2*Lh*sin(angle));
LineTo(x+Lh*(2*Cos(angle)+cos(angle+Pi/6)/3),y+lh*(2*sin(angle)+sin(angle+Pi/6)/3)); //Вторая
ветка вправо
end;
После
всего сделанного остаётся только
написать обработчик события нажатия
клавиши, в котором вызвать первый раз
процедуру с приблизительно следующими
параметрами: координаты – середина
формы по x и её низ по y; Длина – чуть
меньше высоты формы делённая на 3; угол
– вертикально вверх {в Delphi это будет
–Pi/2}; А уровень достаточно считать из
TEdit.
В конце лишь хочу заметить тот
факт, что работа будет происходить
медленно на уровнях выше 9, т.к. вся работа
происходит параллельно: высчитывание
координат по формулам для чисел с
плавающей точкой, обращение к секторам
винчестера, да и собственно сам процесс
рисования на полотне – всё это очень
трудоёмко, когда речь идёт о 9 уровне
вложенности процедуры самой в себя. {4
в степени (9-1) + 1 = 65'537 — количество
вызванных нами процедур. Для понимающего
человека это исчерпывающее объяснение.}
Поэтому при следующей нашей встрече я
опишу иной, более последовательный
способ обработки информации.
Фрактал, Фракталы, Программирование, часть 1
Побудова
фрактальних зображень


