
- •2. Понятие и виды коррел. И регресс. Задачи коррел. И регресс. Ан-за
- •3. Парн. Лин. Регресс.(плр)
- •5.Коэф-т корреляции
- •6.Предпос. М-да наим. Квадратов. Т. Г-м
- •7.Анализ точности опред. Оценок коэф-ов регрессии.
- •1. Понятие экон-ки. Осн. Задачи экон-ки.
- •8) Проверка гипотез относит. Коэф-тов лин. Ур-я регрес
- •9. Интерв. Оценки коэф-ов лин. Ур-ния регрессии
- •13. Расчет коэф-в множ. Регр-ии.
- •24/Обратная модель.
- •14. Дисперсии и станд. Ошибки коэф-в.
- •19. Проверка равенства двух коэффициентов детерминации.
- •20. Проверка гипотезы о совпадении уравнений регрессии для двух выборок
- •21. Статистика Дарбина-Уртсона
- •22.Логарифмические (лог-линейные) модели.
- •33. Метод лин.Комбинаций част.Критериев.
- •34. Метод ведущего критерия.
- •36. Метод равных и наим-их относит. Отклонени
- •37. Метод минимакса
- •38. Предмет и основные понятия теории игр
- •42. Решение матричных игр в смешанных стратегиях. Теорема о необходимом и достаточном условии смешанных стратегий
- •43.Теорема о преобразованиях эл-ов платежной матрицы
- •16. Пров стат значимости коэф ур-ния множ лин регрессии
- •44. Теорема о сведении плат-й матрицы к матрице с полож числами.
- •45. Сведение матричной игры к задаче линейного программирования
- •46. Игры с природой. Понятие риска сиатистика. Матрица рисков.
- •47. Критерии Байеса и Лапласа выбора наилучшей стратегии статистика
- •48. Критерии Вальда, Сэвиджа и Гурвица выбора наилучшей стратегии статистика.
- •49. Модели анализа основных финансовых операций.
- •50. Дисконтирование денежных потоков. Текущая стоимость проекта.
- •51. Чистая текущая стоимость инвестиционного проекта
- •52. Внутренняя норма прибыли проекта
- •Вопрос 53. Индекс прибыльности и период окупаемости проекта.
- •Вопрос 54. Влияние инфляции на денежные потоки проекта.
- •58. Осн. Понятия и опр. Спу
- •57.Анализ чувств-ти ден. Потоков проекта
- •17, 18. Проверка общ кач-ва ур множ рег-сии и статзначимостикоэф детерминации.
- •59. Правила построения сет. Графиков
- •60. Расч. Врем. Парам. Событ.
- •63. Оптимизация проекта по времени, если задан срок выполнения проекта
- •62. Линейный график комплекса работ (график Ганта). Диаграмма потребления ресурсов
- •61. Расч времен парам раб.
- •64. Оптимизац проекта по времени за счет вложен выделен сумм.Ср.
- •65. Оптимизация проекта по стоимости при нефиксированной величине критического пути.
- •66. Оптимизация проекта по стоимости при фиксированной величине критического пути
- •67. Оптимизация проекта по ресурсам
- •70. Основные соотношения, отражающие сущность моб.
- •71. Мат. Модель моб. Эк. Сущность коэф-тов прямых затрат (кпз).
- •72Испол.Моб в исслед.Взаимосв. Отрасл.Структур
- •73. Использование модели моб в прогноз.Цен
- •68.Принципиальная схема моб в снс.
- •69. Экономическое содержание квадрантов моб.
7.Анализ точности опред. Оценок коэф-ов регрессии.
Оценки
коэффициентов регрессии
 и
и является
тем надёжнее, чем < их дисперсии Д(
является
тем надёжнее, чем < их дисперсии Д( )
и Д(
)
и Д(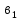 ),
т.е. чем < их разброс вокруг
),
т.е. чем < их разброс вокруг и
и .
.
Надёжность
оценок тесно связана с дисперсией
случайных отклонений. Фактически Д( )=
)= явл. дисперсией Д(У/
явл. дисперсией Д(У/ )
случайной переменной У.
)
случайной переменной У.
Выведем формулы связей дисперсий оценок коэффициентов с дисперсией случайных отклонений.
Для
этого преставим формулы для определения
 и
и
 в виде линейных функций относительно
значений переменных У.
в виде линейных функций относительно
значений переменных У.
 =
= =
= ,
т.к.
,
т.к.
Обозначим
 через
через
 ,
тогда
,
тогда

 ,
где
,
где

Т.к.
предполагается, что дисперсия У постоянна
и не зависит от Х, то
 и
и можно рассмотреть как некоторые пост.,
следовательно дисперсия
можно рассмотреть как некоторые пост.,
следовательно дисперсия
Д( =
Д(
=
Д( =
= =
= (1)
(1)
Д( =
Д(
=
Д( =
= .
(2)
.
(2)
Из формул 1 и 2 видно, что:
1.)дисперсия оценок прямо пропорциональна дисперсии случайного отклонения следовательно чем больше фактор случайности, тем менее точными будут оценки;
2.) чем больше число наблюдений n, тем более точными будут оценки;
3.) чем больше дисперсия объясняющей переменной, тем менее дисперсия оценок коэф-ов.
Но
т.к. случайные отклонения
 по выборке определены быть не могут, то
при анализе надёжности оценок, она
заменяется оценками.
по выборке определены быть не могут, то
при анализе надёжности оценок, она
заменяется оценками.
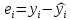 =
= ,
а их дисперсии заменяются несмещённой
оценкой.
,
а их дисперсии заменяются несмещённой
оценкой.
 в
этом случае выборочные исправленные
дисперсии будут иметь вид:Д (
в
этом случае выборочные исправленные
дисперсии будут иметь вид:Д ( Д
(
Д
( =
=
 необъяснённая
дисперсия, т.е. это доля разброса зависимой
переменной, кот. не объясняется регрессией.
необъяснённая
дисперсия, т.е. это доля разброса зависимой
переменной, кот. не объясняется регрессией.
S= - стандартная ошибка регрессии
- стандартная ошибка регрессии
S =
=
 иS
иS =
= -
стандартные ошибки оценок коэффициентов
регрессии.
-
стандартные ошибки оценок коэффициентов
регрессии.
1. Понятие экон-ки. Осн. Задачи экон-ки.
Экон-ка (измер. в эконом.)- наука, в кот. на основ. реальн. стат. дан. строятся, анализ. и соверш-ся мат. модели реальн. эк. явл. и проц-в.Объект исслед.-эк. явл. и проц.
Предмет-их коллич. хар-ки и показат.Экон-ка появ-сь на осн. эк. теории, мат. экономики, эк. и мат. стат-ки.
задачи:
1)постр. эконометрич. моделей-этап спецификац.
2)оценка параметров постр-ой модели-этап параметризации
3)проверка кач-ва найден. парам-в модели и самой модели-этап верификац.4)исп. постр-х моделей для объясн. поведения исслед-х эк. показат. для прогноз-ния, а также для провед. осмысл.эк. политики.
8) Проверка гипотез относит. Коэф-тов лин. Ур-я регрес
При
стат. анализе возник. необх-ть сравнения
эмпирич.значений коэф-тов с теоретич.
ожидаемыми их значениями. Такой анализ
осущ-ся по схеме статистич. проверки
гипотез.Гипотеза
 ,
подлежащая проверке, наз-ся основой(нулевой).
Гипотеза
,
подлежащая проверке, наз-ся основой(нулевой).
Гипотеза ,
которая будет приниматься, если отклонится
,
которая будет приниматься, если отклонится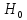 наз-ся альтернативной (конкурирующей).
наз-ся альтернативной (конкурирующей).
Для
проверки гипотезы
 :
: =
= ;
; :
: ≠
≠ ,строитсяt-статистика
по формуле
,строитсяt-статистика
по формуле
 =(в0-β)/
=(в0-β)/ .
При справедливости гипотезы
.
При справедливости гипотезы она имеет распределение Стьюдента с
числом степеней свободы ν=n-2,
где
n-объем
выборки. По числу степеней свободы и
заданному ур-ню значимости α по таблицам
критич. точек нах-ся критич. значение
она имеет распределение Стьюдента с
числом степеней свободы ν=n-2,
где
n-объем
выборки. По числу степеней свободы и
заданному ур-ню значимости α по таблицам
критич. точек нах-ся критич. значение
 Гипотеза
Гипотеза отклоняется,
если│
отклоняется,
если│ │≥
│≥ (для
коэф-та
(для
коэф-та аналогично).
аналогично).
На
начальном этапе статистич. анализа
более важной задачей явл-ся установление
линейн. связи между переменными X,Y.Эта
задача решается аналогично:
 :
: =0;
=0; :
: ≠0.
≠0.
 =
= :
: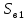 ;
│
;
│ │≥
│≥ ,
то гипотеза
,
то гипотеза отклоняется.
Данную гипотезу называют гипотезой о
статистич. значимости коэф-та регрессии.
Если
отклоняется.
Данную гипотезу называют гипотезой о
статистич. значимости коэф-та регрессии.
Если приним-ся,
приним-ся, -статистически
незначим.Чтобы определить статистич.
значимость можно не пользоваться
таблицами:
-статистически
незначим.Чтобы определить статистич.
значимость можно не пользоваться
таблицами:
Если
│t│ 1-то
в этом случае коэф-т не может быть признан
значимым. Доверительная вероят-ть
составит меньше чем 0,7 Если 1˂│t│
1-то
в этом случае коэф-т не может быть признан
значимым. Доверительная вероят-ть
составит меньше чем 0,7 Если 1˂│t│ 2-
то найденная оценка может рассматриваться
как слабозначимая. В этом случае доверит.
вероят-ть нах-ся в пределах 0,7 и 0,95.Если
2˂│t│
2-
то найденная оценка может рассматриваться
как слабозначимая. В этом случае доверит.
вероят-ть нах-ся в пределах 0,7 и 0,95.Если
2˂│t│ 3-
то в этом случае говорят о сильной
линейной зависимостиX
и Y.Доверительная
вероят-ть от 0,95 до 0,99.Если │t│
3-
то в этом случае говорят о сильной
линейной зависимостиX
и Y.Доверительная
вероят-ть от 0,95 до 0,99.Если │t│ 3-очень
сильная линейная зависимость.
3-очень
сильная линейная зависимость.
