
- •2. Понятие и виды коррел. И регресс. Задачи коррел. И регресс. Ан-за
- •3. Парн. Лин. Регресс.(плр)
- •5.Коэф-т корреляции
- •6.Предпос. М-да наим. Квадратов. Т. Г-м
- •7.Анализ точности опред. Оценок коэф-ов регрессии.
- •1. Понятие экон-ки. Осн. Задачи экон-ки.
- •8) Проверка гипотез относит. Коэф-тов лин. Ур-я регрес
- •9. Интерв. Оценки коэф-ов лин. Ур-ния регрессии
- •13. Расчет коэф-в множ. Регр-ии.
- •24/Обратная модель.
- •14. Дисперсии и станд. Ошибки коэф-в.
- •19. Проверка равенства двух коэффициентов детерминации.
- •20. Проверка гипотезы о совпадении уравнений регрессии для двух выборок
- •21. Статистика Дарбина-Уртсона
- •22.Логарифмические (лог-линейные) модели.
- •33. Метод лин.Комбинаций част.Критериев.
- •34. Метод ведущего критерия.
- •36. Метод равных и наим-их относит. Отклонени
- •37. Метод минимакса
- •38. Предмет и основные понятия теории игр
- •42. Решение матричных игр в смешанных стратегиях. Теорема о необходимом и достаточном условии смешанных стратегий
- •43.Теорема о преобразованиях эл-ов платежной матрицы
- •16. Пров стат значимости коэф ур-ния множ лин регрессии
- •44. Теорема о сведении плат-й матрицы к матрице с полож числами.
- •45. Сведение матричной игры к задаче линейного программирования
- •46. Игры с природой. Понятие риска сиатистика. Матрица рисков.
- •47. Критерии Байеса и Лапласа выбора наилучшей стратегии статистика
- •48. Критерии Вальда, Сэвиджа и Гурвица выбора наилучшей стратегии статистика.
- •49. Модели анализа основных финансовых операций.
- •50. Дисконтирование денежных потоков. Текущая стоимость проекта.
- •51. Чистая текущая стоимость инвестиционного проекта
- •52. Внутренняя норма прибыли проекта
- •Вопрос 53. Индекс прибыльности и период окупаемости проекта.
- •Вопрос 54. Влияние инфляции на денежные потоки проекта.
- •58. Осн. Понятия и опр. Спу
- •57.Анализ чувств-ти ден. Потоков проекта
- •17, 18. Проверка общ кач-ва ур множ рег-сии и статзначимостикоэф детерминации.
- •59. Правила построения сет. Графиков
- •60. Расч. Врем. Парам. Событ.
- •63. Оптимизация проекта по времени, если задан срок выполнения проекта
- •62. Линейный график комплекса работ (график Ганта). Диаграмма потребления ресурсов
- •61. Расч времен парам раб.
- •64. Оптимизац проекта по времени за счет вложен выделен сумм.Ср.
- •65. Оптимизация проекта по стоимости при нефиксированной величине критического пути.
- •66. Оптимизация проекта по стоимости при фиксированной величине критического пути
- •67. Оптимизация проекта по ресурсам
- •70. Основные соотношения, отражающие сущность моб.
- •71. Мат. Модель моб. Эк. Сущность коэф-тов прямых затрат (кпз).
- •72Испол.Моб в исслед.Взаимосв. Отрасл.Структур
- •73. Использование модели моб в прогноз.Цен
- •68.Принципиальная схема моб в снс.
- •69. Экономическое содержание квадрантов моб.
66. Оптимизация проекта по стоимости при фиксированной величине критического пути
Пусть для каждой работы известны след. данные:
 -
мин. прод-ть выполн. раб., кот. соотв.
наименьшие затраты
-
мин. прод-ть выполн. раб., кот. соотв.
наименьшие затраты
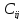 .
.
 -норм.
прод-ть, кот. будут соответств. наименьшие
затраты
-норм.
прод-ть, кот. будут соответств. наименьшие
затраты
 .
.
Будем считать, что затраты на выполнение отд. работ нах-ся в обратной зав-ти от прод-ти их выплн-я.
К-м
доп. затрат (КДЗ) будем считать к-т, кот.
нах-ся по форм.
 и
показывает, насколько увел-ся ст-ть
работы (ij)при
уменьшении времени её выполнения на
одну ед.
и
показывает, насколько увел-ся ст-ть
работы (ij)при
уменьшении времени её выполнения на
одну ед.
Пусть
задан сетевой гр. проекта. Известны
прод-ти выполнения работ и их ст-ть в
срочном режиме (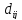 ;
; ).
).
Понятно,
что в этом сл. cт-ть
проекта будет наиб-й, а время вып-я
наименьшим. Ставится задача миним-и
ст-ти проекта за счёт увеличения времени
отд. работ при фиксир. сроке t0
. В этом сл. tкр.
может быть < заданного срока или равно
ему. Если
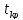 =t0
, то в этом сл. оптим-я возможна только
за счёт резервов некрит. работ, а если
=t0
, то в этом сл. оптим-я возможна только
за счёт резервов некрит. работ, а если
 <0,
то за счёт резервов всех работ проекта.
После оптим-и все работы будут крит-ми,
т.к. их прод-ти будутдостигать наиб-х
возм. значений. Ни одно событие, ни одна
работа не будут иметь резерва. Такой
план наз-ся безерезервным. Здесь ранние
и поздние сроки свершения событий будут
совпадать, а времена начала и окончания
работ будут совпадать со сроками
свершения событий, поэтому неизв. задачи
будем считать сроки свершения событий.
Прод-ть выпол-я кажд. работы в оптим.
плане опр-ся как разность , а ст-ть вып-я
работ будет опр-ся по формуле
<0,
то за счёт резервов всех работ проекта.
После оптим-и все работы будут крит-ми,
т.к. их прод-ти будутдостигать наиб-х
возм. значений. Ни одно событие, ни одна
работа не будут иметь резерва. Такой
план наз-ся безерезервным. Здесь ранние
и поздние сроки свершения событий будут
совпадать, а времена начала и окончания
работ будут совпадать со сроками
свершения событий, поэтому неизв. задачи
будем считать сроки свершения событий.
Прод-ть выпол-я кажд. работы в оптим.
плане опр-ся как разность , а ст-ть вып-я
работ будет опр-ся по формуле
 .
.
След-но, модель задачи запишется в виде:

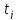 -
- >=
>= ,
(i;j)∊
,
(i;j)∊
 =0,
=0,
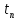 <=
<=
67. Оптимизация проекта по ресурсам
Данная задача явл-ся осн. задачей при планир-и.
Пусть
задан сет. график проекта: G=(E; ).
Кол-во ресурсов =R.
Для каждой работы будут приписаны 2
числа: 1. Прод-ть вып-я работы (
).
Кол-во ресурсов =R.
Для каждой работы будут приписаны 2
числа: 1. Прод-ть вып-я работы ( );
2.
);
2. –
интенсивность потр. рес-в, т.е. кол-во
ресурса, кот. необходимо для вып-я работ
(i;j).
Требуется так разместить работы во
времени, чтобы в любой момент времени
было дост. кол-во ресурса и при этом
время вып-я всего комплекса работ было
мин-м.
–
интенсивность потр. рес-в, т.е. кол-во
ресурса, кот. необходимо для вып-я работ
(i;j).
Требуется так разместить работы во
времени, чтобы в любой момент времени
было дост. кол-во ресурса и при этом
время вып-я всего комплекса работ было
мин-м.
Алгоритм
Предв. шаг: по сет. гр. составляем лин., по кот. опр-м крит. время и крит. путь.
1. 1 проецир-м на ось времени начало и конец кажд. работы. На каждом врем. отрезке опр-м суммарное кол-во потр-го ресурса.
1.2
рассматриваем отрезок [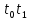 ]
. Над этим отрезком рассм-м все работы.
Нумеруем эти работы в порядке возрастания
их полных резервов времени. Работы с
одинаковыми полными резервами нумеруем
в порядке убывания интенсивности.
]
. Над этим отрезком рассм-м все работы.
Нумеруем эти работы в порядке возрастания
их полных резервов времени. Работы с
одинаковыми полными резервами нумеруем
в порядке убывания интенсивности.
1.3 в порядке присвоенных номеров послед-но суммируем инт-ти работ и сравниваем полученные суммы с заданной величиной ресурса. Если после прибавления инт-ти оосн. работ сумма превосходит R, то эта работа сдвигается вправо на вел-ну рассматр. отрезка. Переходим к добавлению инт-ти очередной работы.
Общий шаг:
1.
Рассматриваем отрезок [ ;
; ].
Рассм. все работы, лежащие над этим
отрезком. Нумеруем эти работы, но в
первую очередь нумеруются работы, кот.
нач-ся левее начала отрезка. Эти работы
нумеруются в порядке возрастания
разности между остальными резервами
этих работ и концом отрезка. Ост. работы
нум-ся согл. 1-го шага.
].
Рассм. все работы, лежащие над этим
отрезком. Нумеруем эти работы, но в
первую очередь нумеруются работы, кот.
нач-ся левее начала отрезка. Эти работы
нумеруются в порядке возрастания
разности между остальными резервами
этих работ и концом отрезка. Ост. работы
нум-ся согл. 1-го шага.
2. пунк 3 1-го шага.
