60. Расч. Врем. Парам. Событ.

Ранн. срок совершен. событ. j – t _p(j) - самый ранн. момент врем., к к-му заверш. все предшеств. этому событ. раб.

Будем счит. t _p(1) =0, а все послед. ранн. срок. событ. будем опред-ть по ф-ле:, - множ. работ, вход. в j-ое событ.

Поздн. срок свершен. событ. i, 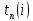- сам. поздн. мом-т врем, после к-го остает. ровно стольк. врем., скольк. надо для завершен. всех раб. след. за этим событ. , а все остав-ся определ разност. м/ду и длин максим из след путей , -множ. раб. выход. из i-го событ.

Резерв времен. соб i (R(i)) – разн-ть м/ду поздн и ранн срок. совершен. событ.:

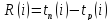Все раб. событ., лежащ на крит. пути имеют нулев. резерв врем.

При расч времен парамет событ. удобно пользов. 4-х секторн схем .

1. В верхн сектор. проставл № событ.

2. Рассматр-ем событ. в порядке возрастан. № и считая, что t _p(1) =0. По ф-ле по входящ. в событ. раб. опр-ем и запис-ем в лев. сектор.

3. Перепис. в заверш. событ. число из лев. сект. в прав. и по обратн. №№ событ. по ф-ле по выходн. раб. опр-ем . Там, гдеR(i)=0 – крит. путь.

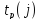
63. Оптимизация проекта по времени, если задан срок выполнения проекта

Пусть задан срок выполнения проекта t0, а расчетное время tкр больше t0 (tкр>t0)/ В этом случае оптимизация комплекса работ сводится к сокращению продолжительности критического пути. Это сокращение может быть достигнуто либо за счет перераспределения внутренних резервов, либо за счет привлечения дополнительных средств.

Рассмотрим 2 постановки задачи оптимизации проектов по времени с использованием дополнительных средств.

Задача1. Пусть задан сетевой график проекта g=(E,e).Время выполнения каждой работы обозначим tij. Вложения дополнительных средств x_ij в работу (i , о)сокращает ее выполнение до значения t_ij = t_ij – x_ij * k_{ij ,} k_ij – технологические коэффициенты использования дополнительных средств. Сокращение продолжительности работы не беспредельно. Существует минимально возможное время ее выполнения d_ij . Требуется найти величины дополнительных вложений в каждую работу x_ij , а также время начала t_ij и окончание t⁰_ij каждой работы , чтобы общая сумма привлеченных дополнительных средств была минимальной, а время выполнения всего комплекса работ не превосходила t₀.

Min F= ∑x_ij

≤t₀ , (i, n) є

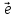
t_ij⁰ – tⁿ_ij ≥d_{ij ,} (i, n) є

t_ij⁰ – tⁿ_ij = t_ij – x_ij * k_ij , (i, n) є

t_jr≥ t_ij⁰ , i, j, r є E

x_ij ≥ 0, tⁿ_ij ≥ 0 , t_ij⁰≥ 0 , (i, n) є

Пример : Проект представлен следующим сетевым графиком

Для каждой работы известны 2 числа : продолжительность выполнения ( 1-ое число), минимальное возможное время выполнения ( 2-ое число).

Задано время выполнения проекта t₀=22 , технологические коэффициенты использования дополнительных средств

k₁₂=0,1 k₁₃=0,5

k₂₃=0,1 k₂₄=0,3

k₃₅=0,2 k₄₅=0,5

x_ij=? , tⁿ , t⁰ →min

Решение :

Min F = x₁₂+x₁₃+x₂₃+x₂₄+x₃₅+x₄₅

T⁰₃₅≤22, t⁰₄₅≤22

t⁰₁₂- tⁿ₁₂≥4, t⁰₁₃-tⁿ₁₃≥6, t⁰₂₃- tⁿ₂₃≥5

t⁰₂₄-tⁿ₂₄≥4, t⁰₃₄- tⁿ₃₄=0, t⁰₃₅-tⁿ₃₅≥3, t⁰₄₅-tⁿ₄₅≥7

t⁰₁₂- tⁿ₁₂=6-0,1*x₁₂, t⁰₁₃-tⁿ₁₃=10 – 0,5x₁₃

t⁰₂₃- tⁿ₂₃=12-0,1x₂₃, t⁰₂₄-tⁿ₂₄=8 – 0,3x₂₄

t⁰₃₅-tⁿ₃₅=6-0,2x₃₅ , t⁰₄₅-tⁿ₄₅ = 9- 0,5x₄₅

tⁿ₁₂= tⁿ₁₃=0

tⁿ₂₃≥ t⁰₁₂ tⁿ₂₄≥ t⁰₁₂

tⁿ₃₄≥ t⁰₁₃ , tⁿ₃₄≥ t⁰₂₃

tⁿ₃₅≥ t⁰₁₃, tⁿ₃₅≥ t⁰₂₃

tⁿ₄₅≥ t⁰₂₄, tⁿ₄₅≥ t⁰₃₄

x_ij≥0, tⁿ_ij≥0, t⁰_ij≥0 (i, n) є