- •2. Понятие и виды коррел. И регресс. Задачи коррел. И регресс. Ан-за
- •3. Парн. Лин. Регресс.(плр)
- •5.Коэф-т корреляции
- •6.Предпос. М-да наим. Квадратов. Т. Г-м
- •7.Анализ точности опред. Оценок коэф-ов регрессии.
- •1. Понятие экон-ки. Осн. Задачи экон-ки.
- •8) Проверка гипотез относит. Коэф-тов лин. Ур-я регрес
- •9. Интерв. Оценки коэф-ов лин. Ур-ния регрессии
- •13. Расчет коэф-в множ. Регр-ии.
- •24/Обратная модель.
- •14. Дисперсии и станд. Ошибки коэф-в.
- •19. Проверка равенства двух коэффициентов детерминации.
- •20. Проверка гипотезы о совпадении уравнений регрессии для двух выборок
- •21. Статистика Дарбина-Уртсона
- •22.Логарифмические (лог-линейные) модели.
- •33. Метод лин.Комбинаций част.Критериев.
- •34. Метод ведущего критерия.
- •36. Метод равных и наим-их относит. Отклонени
- •37. Метод минимакса
- •38. Предмет и основные понятия теории игр
- •42. Решение матричных игр в смешанных стратегиях. Теорема о необходимом и достаточном условии смешанных стратегий
- •43.Теорема о преобразованиях эл-ов платежной матрицы
- •16. Пров стат значимости коэф ур-ния множ лин регрессии
- •44. Теорема о сведении плат-й матрицы к матрице с полож числами.
- •45. Сведение матричной игры к задаче линейного программирования
- •46. Игры с природой. Понятие риска сиатистика. Матрица рисков.
- •47. Критерии Байеса и Лапласа выбора наилучшей стратегии статистика
- •48. Критерии Вальда, Сэвиджа и Гурвица выбора наилучшей стратегии статистика.
- •49. Модели анализа основных финансовых операций.
- •50. Дисконтирование денежных потоков. Текущая стоимость проекта.
- •51. Чистая текущая стоимость инвестиционного проекта
- •52. Внутренняя норма прибыли проекта
- •Вопрос 53. Индекс прибыльности и период окупаемости проекта.
- •Вопрос 54. Влияние инфляции на денежные потоки проекта.
- •58. Осн. Понятия и опр. Спу
- •57.Анализ чувств-ти ден. Потоков проекта
- •17, 18. Проверка общ кач-ва ур множ рег-сии и статзначимостикоэф детерминации.
- •59. Правила построения сет. Графиков
- •60. Расч. Врем. Парам. Событ.
- •63. Оптимизация проекта по времени, если задан срок выполнения проекта
- •62. Линейный график комплекса работ (график Ганта). Диаграмма потребления ресурсов
- •61. Расч времен парам раб.
- •64. Оптимизац проекта по времени за счет вложен выделен сумм.Ср.
- •65. Оптимизация проекта по стоимости при нефиксированной величине критического пути.
- •66. Оптимизация проекта по стоимости при фиксированной величине критического пути
- •67. Оптимизация проекта по ресурсам
- •70. Основные соотношения, отражающие сущность моб.
- •71. Мат. Модель моб. Эк. Сущность коэф-тов прямых затрат (кпз).
- •72Испол.Моб в исслед.Взаимосв. Отрасл.Структур
- •73. Использование модели моб в прогноз.Цен
- •68.Принципиальная схема моб в снс.
- •69. Экономическое содержание квадрантов моб.
47. Критерии Байеса и Лапласа выбора наилучшей стратегии статистика
К первой группе относительных критериев, в которых используются вероятности состояний природы, относятся критерии Байеса и Лапласа. В качестве оптимальной по критерию Байеса принято считать стратегию при которой максимизируется средний выигрыш статистика
Max ai = max (i) ∑(j=1,n)aijqj , i = 1,m
Если статистик представляет в равной мере правдоподобными все состояния природы q1=q2=….=qn=1/n, то по критерию Лапласа в качестве оптимальной берется стратегия обеспечичвающая max ai = max 1/n ∑(j=1,n)aij , i = 1,m
48. Критерии Вальда, Сэвиджа и Гурвица выбора наилучшей стратегии статистика.
По критерию Вайда (критерий крайнего пессимизма) в качестве оптимальной считается стратегия, при которой в наихудших условиях гарантируется максимальный выигрыш:
v=maxi
minj
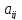 .
.
По критерию Сэвиджа (критерий минимального риска) в качестве оптимальной рекомендуется выбирать стратегию, для которого величина максимального риска минимизируется:
r=minj
maxi
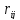 .
.
По критерию Гурвица в качестве оптимальной следует выбирать стратегию, для которой выполняется соотношение:
g=maxi
[αminj
 + (1-α)maxj
+ (1-α)maxj
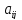 ],
где 0>α>1.
],
где 0>α>1.
Если α=0, то получим критерий крайнего оптимизма.
Если α=1, то получим критерий Вайда.
49. Модели анализа основных финансовых операций.
Пусть
Р – начальный капитал, положенный в
банк при годовой %-ной ставке r.
Тогда в конце периода капитализации
наращенная сумма, т.е. сумма начального
капитала и %-тов, составит Р(1+r),
где r
выражена в долях.В конце 2 периода
капитализации наращенная сумма составит
 .В
общем случае наращенная сумма за n
периодов капитализации будет равна
.В
общем случае наращенная сумма за n
периодов капитализации будет равна
 –1.
–1.
Наращенная сумма называется будущей стоимостью начального капитала (FV).
Коэф.
 называется коэф. аккумуляции, который
показывает денежную сумму нарастающую
заn
периодов капитализации при начальном
капитале 1 ден. ед.
называется коэф. аккумуляции, который
показывает денежную сумму нарастающую
заn
периодов капитализации при начальном
капитале 1 ден. ед.
Из
формулы 1
следует,
что
 ,
т.е. для того, чтобы сумма наращенная заn
,
т.е. для того, чтобы сумма наращенная заn
периодов
капитализации составила S
ден. ед. в начале срока нежно положить
в банк
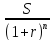 ден. ед.
ден. ед.
Такой начальный капитал, обеспечивающий заданную наращенную сумму называется текущей стоимостью (PV) суммы S.
Следовательно
PV=
 –2.
–2.
Коэф.
δ=
 называется коэф. дисконтирования,
который показывает, какую сумму нужно
положить в банк для того, чтобы черезn
периодов капитализации наращенная
сумма составила 1 ден. ед.
называется коэф. дисконтирования,
который показывает, какую сумму нужно
положить в банк для того, чтобы черезn
периодов капитализации наращенная
сумма составила 1 ден. ед.
50. Дисконтирование денежных потоков. Текущая стоимость проекта.
Инвестиц. проект – любое инвестирование денег, генерирующее денежные потоки в будущем.
Метод дисконтирования денежных потоков инвестиц. проекта является ключевым в современном финансовом анализе, при этом дисконтируются свободные денежные потоки, которые представляют собой разность прибыли и инвестиций в заданном периоде времени.

Предположим,
что инвестиц. проект генерирует
положительные свободные денежные потоки
в течение n
периодов времени:
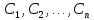 .
.
Начальные
инвестиции в проект равны
 .
.
Временную диаграмму свободных денежных потоков можно представить в виде:
|
Своб ден поток |
|
|
|
… |
|
|
|
Время |
0 |
1 |
2 |
… |
n-1 |
n |
Вместо того, чтобы инвестировать деньги в проект, инвестор может положить некоторую сумму в банк под % с целью получения таких же денежных платежей в будущем.
Текущей стоимостью свободных денежных потоков инвестиц. проекта называется начальный капитал, положенный в банк под %, обеспечивающий последовательность денежных потоков, равных денежным потокам инвестиц. проекта.
 –3.
–3.
Т.о. текущая стоимость инвестиц. проекта равна сумме дисконтированных денежных потоков.
%-ная ставка, используемая при дисконтировании свободных денежных потоков проекта называется нормой (ставкой) дисконтирования.
Банковскую %-ную ставку можно брать в качестве нормы дисконтирования только в том случае, когда риск, связанный с денежными потоками проекта и риск, связанный с банковскими депозитами, равны.