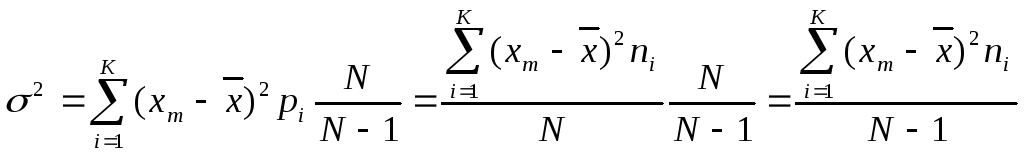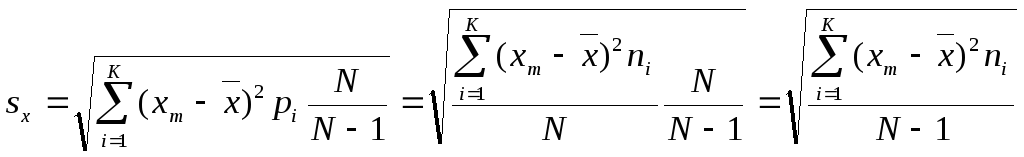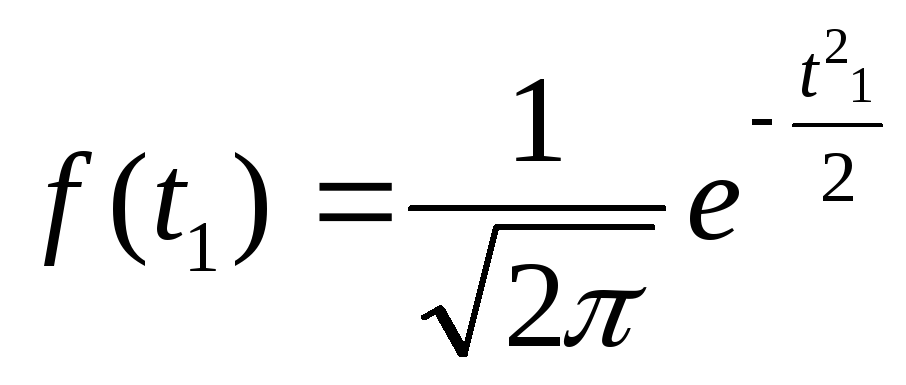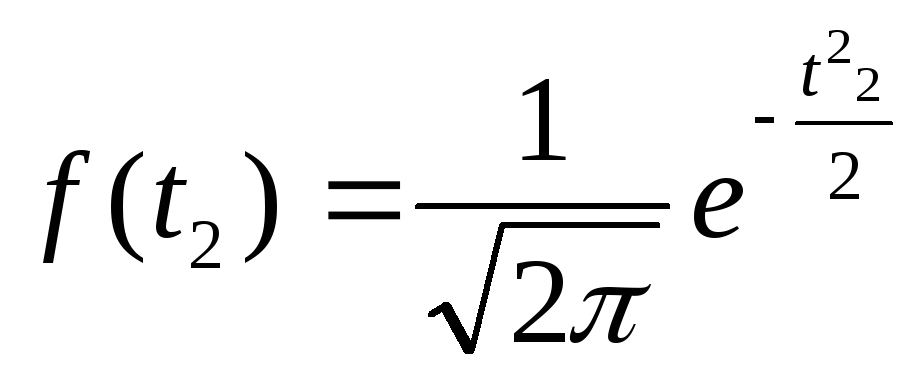Задание для студентов на практическое №7по теме

«Основы математической статистики. Элементы корреляционного анализа»

Цель занятия: Научиться решать примеры и задачи по данной теме

Вопросы теории ( исходный уровень)

1. Основные понятия математической статистики

2. Генеральная совокупность и выборка.

3. Вариационный и интервальный статистические ряды.

4. Полигон частот и гистограмма.

5. Точечная и интервальная оценка параметров генеральной совокупности по данным выборки.

6. Порядок статистической обработки экспериментальных данных.

7. Статистическая обработка данных лабораторного эксперимента.

8. Теория погрешностей.

9. Обработка результатов непосредственных и косвенных измерений

10. Правила оформления результатов лабораторных работ.

11. Элементы корреляционного анализа

(лекция №2)

Содержание занятия:

1.ответить на вопросы по теме занятия

2.решить примеры

Задачи и примеры

Определить соответствие вариационного распределения измеренной величины нормальному закону распределения

1. Произвести измерения N величин и записать результаты измерений в протокол.

2. По результатам измерений построить вариационный ряд.

2.1.- в измеренных величинах найти величину ( х_min) с наименьшим значением и величину (х_max) с наибольшим значением.

2.2.-определить размах вариации R , представляющий собой разность между максимальной и минимальной вариантами совокупности ( R = x_max- x_min).

2.3.-по числу элементов совокупности N определим число классов К на которые следует разбить совокупность измеренных величин. При N≤100 К определим по формуле

K= 1+3,32 lg N, при N›100 К по формуле K= 5 lg N .

2.4.-определить величину классового интервала λ , как частное от деления размаха вариации R на число классов К , λ =R/К = (x_max- x_min)/ К.

Если окажется , что λ=1, собранный материал распределяется в безынтервальный вариационный ряд; если λ≠1, исходные данные необходимо распределить в интервальный ряд. При этом точность величины классового интервала должна соответствовать точности принятой при измерении величин.

2.5.- определить ширину классов входящих в интервальный вариационный ряд в которых расположатся все измеренные величины от x_max до x_min.

Ширина первого класса имеет протяженность от x_min до x_min+λ, т.е.[ x_min ÷ x_min+λ].

Ширина второго класса имеет протяженность от x_min+ λ +10^-5λ до x_min+2λ , т.е.

[ x_min+ λ +10^-5λ ÷ x_min+2λ] , где 10^-5λ незначащее число и применяется для того, чтобы разграничить числа находящиеся на границе классовых интервалов и используется во всех классах для различия начала нового класса от конца предыдущего класса.

Ширина К-того класса имеет протяженность от x_min+(К-1) (λ +10^-5λ ) до x_max, т.е.

[x_min+(К-1) (λ +10^-5λ ) ÷ x_max], где x_max= x_min +К λ.

2.6.- найти среднее значение каждого класса х_m . Среднее значение каждого класса равно полусумме значений начала и конца класса без незначащего числа 10^-5λ, т.е.

х_m=( x_min+(I-1) λ +x_min+Iλ)/2, где I принимает значения от 1 до К (I =1;2;…К).

2.7.- определить количество элементов n из измеренных N величин входящих в каждый класс, т.е. получить n₁, n₂,… n_К

2.8. – определить относительную частоту р_i попадания количества элементов n_i из измеренных N величин в каждый класс, т.е. р_i= n_i/ N. Найти р₁, р₂,… р_К.

3. На основании пункта 2 заполнить таблицу:

N=
xmax= xmin= R = xmax- xmin=
K= 1+3,32 lg N=
λ =R/К = (xmax- xmin)/ К=
Классные интервалы	1	2	…	К
Границы клас-сных интервалов	[ xmin ÷ xmin+λ]	[ xmin+ λ +10-5λ ÷ xmin+2λ]	…	[xmin+(К-1) (λ +10-5λ ) ÷ xmax]
Среднее значе-ние классного интервала хm	xmin+λ/2	xmin+3λ/2	…	xmin+(К+1)λ/2
Количество ве-личин входящих в класс ni	n1	n2	…	nК
Частота попа-дания величин в класс рi= ni/ N	р1= n1/ N	р2= n2/ N	…	рК= nК/ N
(хm)I*pi	(xmin+λ/2)р1	(xmin+3λ/2)р2	…	(xmin+(К+1)λ/2)рК

4. По полученным данным построить графики вариационных рядов.

4.1. - полигон частот; по оси абсцисс откладывают среднее значение классов, по оси ординат частоту попадания величин в класс. Высота перпендикуляров, восставляемых на ось абсцисс, соответствует частоте классов. Соединяя вершины перпендикуляров прямыми линиями, получают геометрическую фигуру в виде многоугольника называемую полигоном распределения частот. Линия соединяющая вершины перпендикуляров, называют вариационной кривой или кривой распределения частот вариационного ряда.

4.2. – гистограмма; по оси абсцисс откладывают границы классовых интервалов , по оси ординат – частоты интервалов. В результате получается совокупность прямоугольников . т.е. гистограмма распределения.

4.3. – кумулята; по оси абсцисс откладывают среднее значение классов, по оси ординат – накопление частоты интервалов ( накопление частот находят последовательным суммированием или кумуляцией частот в направлении от первого класса до конца вариационного ряда , т.е. например в третьем классе накопленная частота будет соответствовать сумме частот трех классов) с последующим соединением точек прямыми линиями, получается график называемый кумулятой. Имеет вид S-образной кривой.

4.4. – огива; по оси абсцисс откладывают частоты , а по оси ординат значение классов с последующим соединением геометрических точек прямыми линиями, полученный график называют огивой.

При построении вариационной кривой масштабы на осях прямоугольных координат следует выбирать с таким расчетом, чтобы основание кривой было в 1,5 –2,0 больше ее высоты.

5. Определить основные характеристики варьирующих величин .

5.1. – средняя арифметическая ; найти произведение среднего значения каждого класса (х_evi) _i на относительную частоту р_i попадания количества элементов n_i из измеренных N величин в каждый класс, т.е. р_i*(х_m)_i. Найти р_1*(х_m) ₁, р_2*(х_m)₂,... р_К*(х_m)_К. и по формуле определить среднее арифметическое

5.2. – дисперсия s_x² или σ²;

5.2.1. - найти отклонение среднего значение каждого класса х_m от среднего арифметического ,т.е.(х_m)_I-,

5.2.2. – возвести в квадрат отклонение среднего значение каждого класса х_m от среднего арифметического ,т.е.[(х_m)_i-]²,

5.2.3. – умножить квадрат отклонений среднего значение каждого класса х_m от среднего арифметического на относительную частоту попадания в класс р_i, т.е.

[ (х_m)_i-]²*р_i и по формуле определить дисперсию;

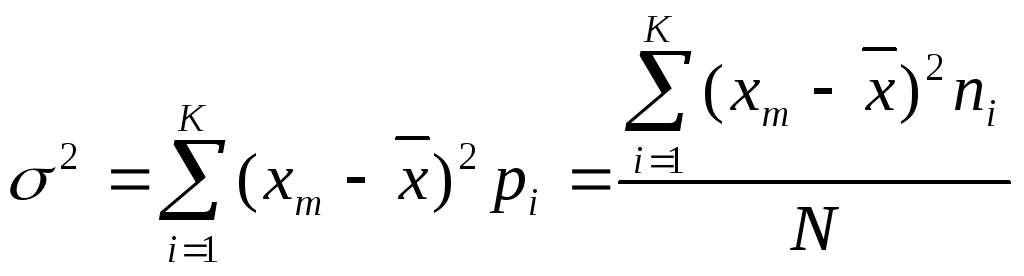
5.2.4.Установлено, что рассчитываемая по формуле дисперсия оказывается смещенной по отношению к своему генеральному параметру на величину , равную N/(N-1). Эта величина называется поправкой Бесселя. Разность (N-1)=k называют числом степеней свободы под которыми понимают число свободно варьирующих величин в составе численно ограниченной совокупности.

Несмещенная дисперсия и среднеквадратичное отклонение определяются;

5.2.4.1. – умножить квадрат отклонений среднего значение каждого класса х_evi от среднего арифметического наколичество элементов n из измеренных N величин входящих в каждый класс, т.е. найти [ (х_m)_i-]²*n_i и по формуле определить несмещенную дисперсию,

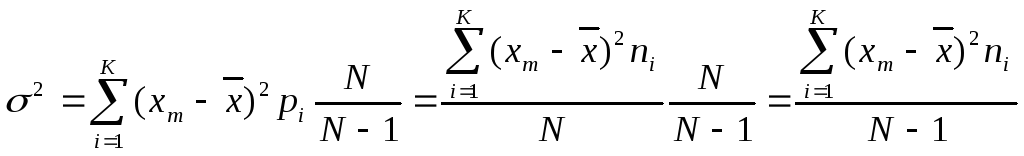
5.2.4.2. – среднее квадратическое отклонение s_x есть показатель, представляющий корень квадратный из дисперсии,

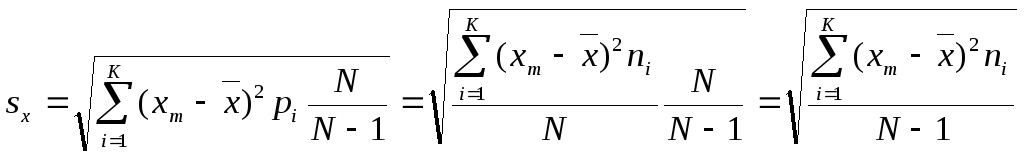
6.На основании пункта 5 заполнить таблицу:

	1	2	…	К
(хm)I-,	(хm)1-,	(хm)2-,	…	(хm)К-,
[ (хm)i-]2,	[ (хm)1-]2	[ (хm)2-]2	…	.[ (хm)К-]2
умножить ква[ (хm)i-]2*рi	[ (хm)1-]2*р1	[ (хm)2-]2*р2	…	[ (хm)К-]2*рК
определить дисперсию
[ (хm)i-]2*ni	[ (хm)1-]2*n1	[ (хm) 2-]2*n2		[ (хm)К-]2*nК
определить несмещенную дисперсию,
Определить среднее квадратическое отклонение sx

7. Определить соответствие вариационного распределения нормальному закону;

7.1. – найти нормированное отклонение t . Отклонение той или иной варианты от средней арифметической, отнесенное к величине среднего квадратического отклонения , называют нормированным отклонением и находят по формуле,

7.1. – Для соответствующих классов найдем функцию нормированного отклонения f(t) по таблице или по формуле,

7.2. – найдем выравнивающие частоты вариационного ряда f^I (t). Для того чтобы ордината выражала не вероятность, а абсолютные значения случайной величины, т.е. выравнивающие частоты вариант эмпирического распределения нужно f^I (t) найти по формуле,

8. На основании пункта 7 заполним таблицу:

	1	2	…	К
нормированное отклонение t			…
нормированного отклонения f(t)			…
выравнивающие частоты вариационного ряда fI (t)			…

9. На графике полигона частот построить точки соответствующие выравнивающей частоте вариационного ряда, вычисленная по нормальному закону.

10. Записать значение исследуемой величины с границами доверительного интервала.

Таблица: Значения функции