Вопрос 3 Спектр непериодического сигнала

Для спектрального представления непериодических сигналов вводится понятие спектральной плотности.

Спектральная плотность – это комплексно-значная функция частоты, одновременно несущая информацию, как об амплитуде, так и о фазе элементарных синусоид.

Спектральная плотность и сигнал связаны между собой парой преобразований Фурье:

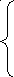
(2.9)

(2.10Поскольку для представления спектров непериодических сигналов используются интегральные преобразования Фурье, эти спектры сплошные.

Спектральная плотность может быть представлена в виде:

Вещественная часть спектральной плотности есть чётная функция частоты:

Мнимая часть спектральной плотности есть нечётная функция частоты:

Если записать спектральную плотность в показательной форме, то можно выделить её модуль и аргумент:

Модуль спектральной плотности называется амплитудным спектром сигнала:

а аргумент спектральной плотности – фазовым спектром сигнала.

Пара преобразований Фурье имеет фундаментальное значение в теории электросвязи, так как многие характеристики сигналов связаны между собой этими преобразованиями.

Все свойства спектральной плотности объединены в основных теоремах о спектрах.

Вопрос 6 Спектр произведения сигналов

Теорема о свёртке.

Как известно, при суммировании сигналов их спектры складываются. Однако спектр произведения сигналов не равен произведению спектров, а выражается некоторым специальным интегральным соотношением между спектрами сомножителей.

Пусть и- два сигнала, для которых известны соответствия,.Образуем произведение этих сигналов:и вычислим его спектральную плотность. По общему правилу:

(2.18)

Применив обратное преобразование Фурье, выразим сигнал через его спектральную плотность и подставим результат в (2.18):

Изменив порядок интегрирования, будем иметь:

откуда:

(2.19)

Интеграл, стоящий в правой части называют свёрткой функций V и U. Символически операция свёртки обозначается как *

Таким образом, спектральная плотность произведения двух сигналов с точностью до постоянного числового множителя равна свёртке спектральных плотностей сомножителей:

(2.20)

Операция свёртки коммутативна, т.е. допускает изменения порядка следования преобразуемых функций:

Теорема о свёртке может быть обращена: если спектральная плотность некоторого сигнала представляется в виде произведения , причёми, то сигналявляется свёрткой сигналови, но уже не в частной , а во временной области:

(2.21)

Вопрос7Равенство Парсеваля

Пусть имеется два вещественных сигнала U(t) и V(t). Назовём взаимным энергетическим спектром двух вещественных сигналов функцию (4.1)

такую что:

(4.2)

причём:

(4.3)

Взаимный энергетический спектр - функция, принимающая в общем случае, комплексные значения:

(4.4)

где - чётная, анечётная функция частоты. Вклад в интеграл даёт только вещественная часть, поэтому:

(4.5)

Последняя формула даёт возможность проанализировать взаимосвязь сигналов. Более того формула (4.5) указывает путь, позволяющий уменьшить связи между двумя сигналами, добившись в пределе их ортогональности. Для этого один из сигналов нужно подвергнуть обработке частотным фильтром. К этому фильтру предъявляется требование не пропускать на выход спектральные составляющие, находящиеся в пределах частотного интервала, где вещественная часть взаимного энергетического спектра велика. Частотная зависимость к-та передачи такого сигнала ортогонализирующего фильтра будет обладать резко выраженным минимумом в пределах указанной области частот.

Если в формуле (4.1) сигналы U(t) и V(t) считать одинаковыми то эта формула приобретает вид:

(4.6)

Величина носит название спектральной плотности энергии сигналаU(t) или, короче, его энергетического спектра. Формула равенства Парсеваля при этом запишется так:

(4.7)

Подход, основанный на спектральном представлении энергии сигнала, выгодно отличается относительной простотой. Энергии, отвечающие различным областям частотной оси, складываются так же, как вещественные числа. Однако, изучая сигнал с помощью его энергетического спектра, мы неизбежно теряем информацию, которая заключается в фазовом спектре сигнала, поскольку в соответствии с формулой (4.6) энергетический спектр есть квадрат модуля спектральной плотности и не зависит от её фазы. Однако понятие энергетического спектра широко применяется для инженерных оценок, устанавливающих ширину спектра сигнала и копи:

Рассмотрим некоторый сигнал, , разложенный в ряд по ортонормированной базисной системе и вычислим его энергию, непосредственно подставив этот ряд в соответствующий интеграл:

(1.13)

Поскольку базисная система функций ортонормирована, в сумме (1.13) отличными от нуля окажутся только члены с номерами . Отсюда получается замечательный результат, который называется равенством Парсеваля:

(1.14)

Смысл этой формулы: энергия сигнала есть сумма энергий всех компонент, из которых складывается обобщённый ряд Фурье.

Для того чтобы выяснить физический смысл дисперсии, положим в (6.24) Тогда поскольку, получаем

(6.26)

Следует подчеркнуть различие между энергетическим спектром детерминированного импульсного сигналаu(t) и спектральной плотностью мощности стационарного случайного процессаX(t). Функция характеризует меру энергии, приходящуюся на единичную полосу частот. В отличие от этого функцияхарактеризует удельную меру мощности. Этот факт находит отражение и в разных физических размерностях данных функций.

Свойства спектральной плотности мощности

1) По своему физическому смыслу спектр мощности вещественен и неотрицателен:

Необходимо указать, что спектральная плотность мощности стационарного случайного процесса, будучи всегда вещественной, не содержит никакой информации о фазовых соотношениях между отдельными спектральными составляющими. Поэтому по спектру мощности принципиально невозможно восстановить какую либо отдельно взятую реализацию случайного процесса.

2) Поскольку чётная функция аргумента, то соответствующий спектр мощностипредставляет собой чётную функцию частоты. Отсюда следует, что пару преобразований Фурье (6.25), (6.26) можно записать, используя лишь интегралы в полубесконечных пределах:

(6.27)

(6.28)