Приближенное вычисление корней

Пусть нужно извлечь корень . Всегда можно подобрать такое целое число, чтобыбыло возможно ближе к, тогда

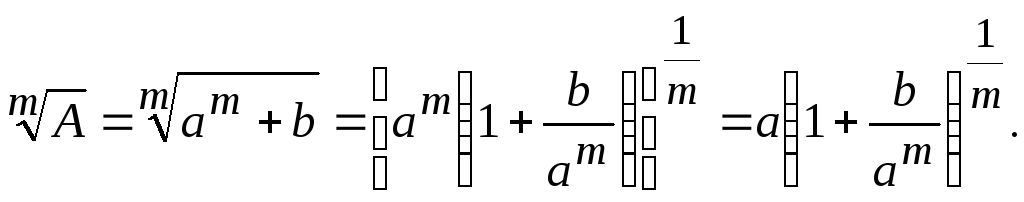
При условии последнее выражение можно вычислить, используя биномиальный ряд:

, .

Пример 24. Вычислить с точностью до 0,0001.

Решение

Используя биномиальный ряд

, при , получим

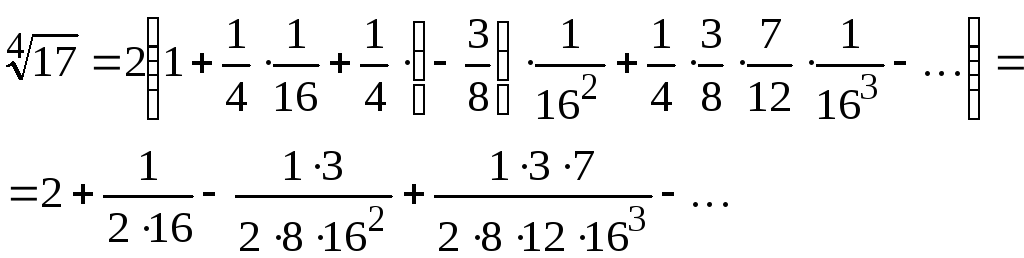
Это знакочередующийся ряд.

; .

Поэтому, ограничившись суммой первых трех членов, получаем .

Приближенное вычисление определенных интегралов

Многие практически нужные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, так как первообразная не может быть выражена через конечное число элементарных функций.

Однако, если подынтегральная функция разлагается в степенной ряд, а пределы интегрирования принадлежат области сходимости, то можно вычислить определенный интеграл с заданной степенью точности.

Пример 25. Вычислить с точностью 0,0001.

Решение

1) Разложим подынтегральную функцию в ряд:

, .

2. Проинтегрируем его почленно

3. Получили знакочередующийся ряд. Для обеспечения требуемой точности достаточно взять сумму первых 7 членов, так как при

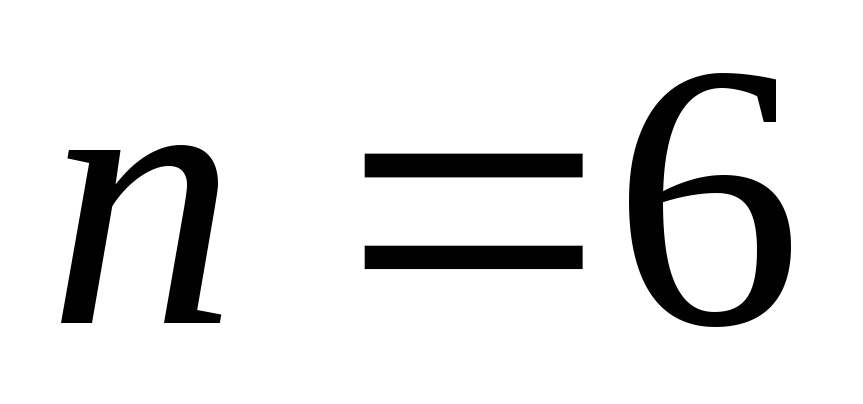
при

.

4) Вычислим приближенно интеграл с одной запасной цифрой.

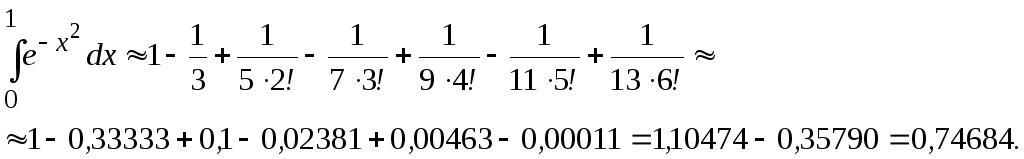
Округляя, получим .

Приближенное решение дифференциальных уравнений

Степенные ряды широко используются при интегрировании дифференциальных уравнений. В этом случае решение задачи Коши

; ;ищется в виде степенного ряда.

Пример 26. Найти первые пять членов разложения в степенной ряд решения задачи Коши ,.

Решение

Так как начальное условие задано при , то

(начальное условие).

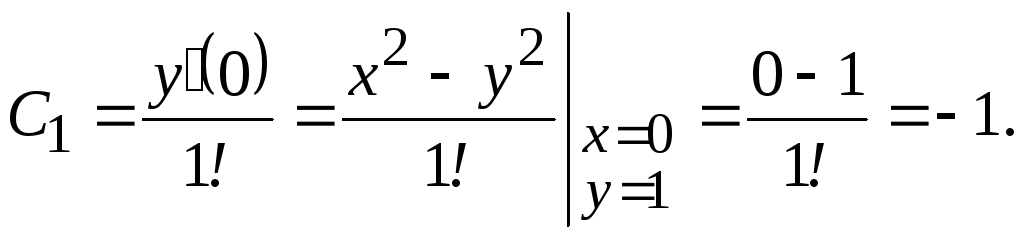
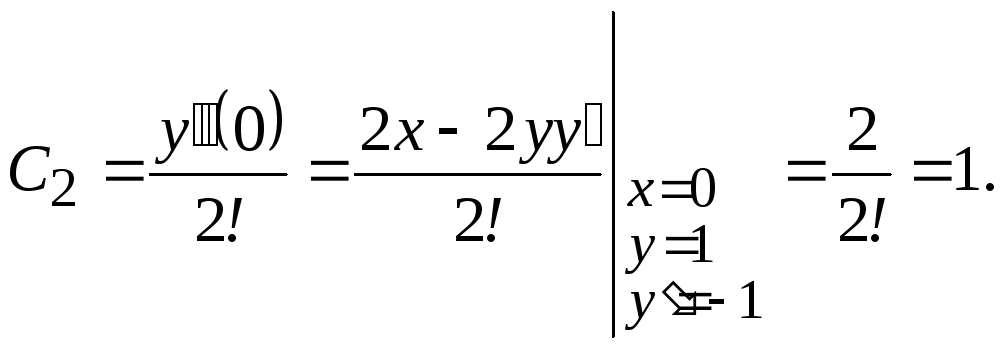
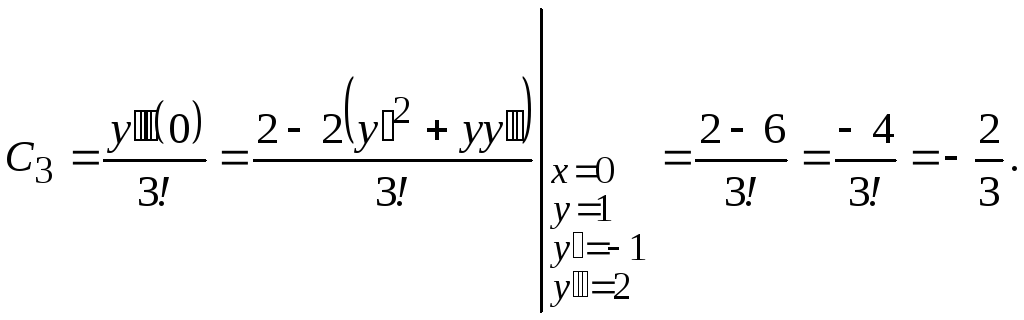
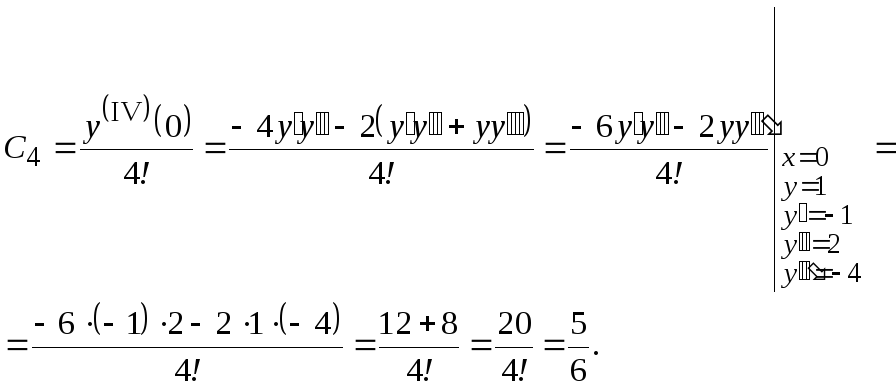
Получаем ряд

Литература

1 Пискунов Н.С. Дифференциальное и интегральное исчисление, т.2. – М.: Наука, 1976 (и последующие издания).

2 Минюк С.А., Самаль С.А., Шевченко Л.И. Высшая математика для экономистов, т.1 – Мн.: Элайда, 2003.

3 Минюк С.А., Ровба Е.А. Высшая математика. – ГрГУ, 2000.

4 Колобов А.М. Избранные главы высшей математики. – Мн.: Высшая школа, 1965.

5 Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 1989.

6 Гусак А.А. Пособие к решению задач по высшей математике. – Мн.: Вышэйшая школа, 1967.

7 Гурский Е.И. Руководство к решению задач по высшей математике. Часть I. – Мн.: Вышэйшая школа, 1989.

С О Д Е Р Ж А Н И Е

ЧИСЛОВЫЕ РЯДЫ Числовой ряд. Общий член ряда Сходящиеся и расходящиеся ряды Основные свойства сходящихся рядов Признаки сходимости числовых рядов Необходимый признак сходимости ряда Знакоположительные числовые ряды Достаточные признаки сходимости знакоположительных рядов ЗНАКОЧЕРЕДУЮЩИЕСЯ И ЗНАКОПЕРЕМЕННЫЕ РЯДЫ Знакочередующиеся ряды Знакопеременные ряды ФУНКЦИОНАЛЬНЫЕ РЯДЫ Функциональный ряд и его область сходимости Степенные ряды РАЗЛОЖЕНИЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ Приближенное вычисление значений некоторых функций Приближенное вычисление корней Приближенное вычисление определенных интегралов Приближенное вычисление дифференциальных уравнений Литература

3 3 3 4 5 5 6 7 15 15 17 20 20 21 24 26 26 28 29 30 31

План 2004/2005, поз.103

Гладкова Галина Александровна

Гладков Лев Львович