
- •Учреждение образования «высший государственный колледж связи» числовые и степенные ряды
- •«Высшая математика»
- •Числовые ряды Числовой ряд. Общий член ряда
- •Сходящиеся и расходящиеся ряды
- •Основные свойства сходящихся рядов
- •Признаки сходимости числовых рядов
- •Необходимый признак сходимости ряда
- •Знакоположительные числовые ряды
- •Достаточные признаки сходимости знакоположительных рядов
- •, , …,, … (8)
- •Знакочередующиеся и знакопеременные ряды Знакочередующиеся ряды
- •Знакопеременные ряды
- •Функциональные ряды Функциональный ряд и его область сходимости
- •Степенные ряды
- •, (15)
- •Разложение элементарных функций в степенные ряды
- •Приближенные вычисления
- •С помощью степенных рядов
- •Приближенное вычисление значений
- •Некоторых функций
- •Приближенное вычисление корней
- •Приближенное вычисление определенных интегралов
- •Приближенное решение дифференциальных уравнений
- •Литература
- •Числовые и степенные ряды
- •«Высшая математика»
- •220114, Г. Минск, ул. Ф. Скорины 8, к.2
Учреждение образования «высший государственный колледж связи» числовые и степенные ряды
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
по дисциплине
«Высшая математика»
для студентов уровней ССО и ВО всех специальностей
Минск 2007
Составители: Г.А. Гладкова, Л.Л. Гладков
Приведен теоретический материал по теме «Числовые и степенные ряды», причем большинство теорем дается с доказательствами. Рассмотрен ряд примеров по исследованию сходимости рядов, а также практическое применение степенных рядов в приближенных вычислениях.
Рецензент: Л.А. Рябенкова
Издание утверждено на заседании кафедры М и Ф
28 апреля 2005 г., протокол № 9
Зав. кафедрой Л.Л. Гладков
Числовые ряды Числовой ряд. Общий член ряда
Определение
Если
дана бесконечная последовательность
чисел
![]() ,
,![]() ,
,![]() ,...,
то выражение вида
,...,
то выражение вида
![]() (1)
(1)
называется
числовым
рядом;
числа
![]() ,
,![]() ,
,![]() ,...–
членами (элементами) ряда,
,...–
членами (элементами) ряда,![]() –
общим членом ряда, если
–
общим членом ряда, если
![]() не зафиксировано.
не зафиксировано.
Пример
1.
Дан ряд
![]() ,
где
общий член
,
где
общий член
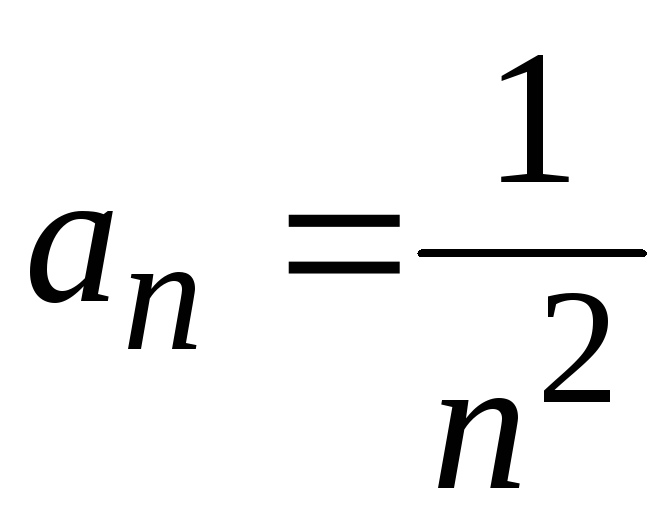 .
Найти
.
Найти![]() .
.
Решение
Заменяя
в общем члене
![]() на
на![]() ,
получим
,
получим![]() .
.
Сходящиеся и расходящиеся ряды
Если
дан ряд (1), то сумма первых n
членов этого ряда называется
![]() ой
частичной суммой
и обозначается через
ой
частичной суммой
и обозначается через
![]() .
Следовательно, суммы
.
Следовательно, суммы
![]() – 1-ая
частичная сумма;
– 1-ая
частичная сумма;
![]() – 2-ая
частичная сумма;
– 2-ая
частичная сумма;
![]() – 3-ая
частичная сумма;
– 3-ая
частичная сумма;
– ……………………….
![]() –
–
![]() ая
частичная сумма;
ая
частичная сумма;
... – ……………………….
образуют
последовательность частичных сумм
![]() ,
,![]() ,
...,
,
...,![]() ,
...
,
...
Определение
Ряд
(1) называется сходящимся,
если существует конечный предел
последовательности частичных сумм, то
есть
![]() .
При этом число
.
При этом число![]() называетсясуммой
ряда.
Если для данного ряда последовательность
частичных
сумм
называетсясуммой
ряда.
Если для данного ряда последовательность
частичных
сумм
![]() не имеет конечного предела при
не имеет конечного предела при![]() ,
то этот ряд называетсярасходящимся.
,
то этот ряд называетсярасходящимся.
Пример 2. Исследовать на сходимость ряд, составленный из членов геометрической прогрессии (геометрический ряд)
![]() ,
,
![]() .
.
Решение
Из
элементарной математики известно, что
сумма n
членов геометрической прогрессии
![]() .
Отсюда следует, что если
.
Отсюда следует, что если![]() ,
то геометрический ряд сходится и его
сумма
,
то геометрический ряд сходится и его
сумма![]() .
Если же
.
Если же![]() ,
то геометрический ряд расходится.
,
то геометрический ряд расходится.
Пример 3. Исследовать на сходимость ряд
![]()
Решение
Так
как
![]() ,
то
,
то![]() ая
частичная сумма данного ряда
ая
частичная сумма данного ряда
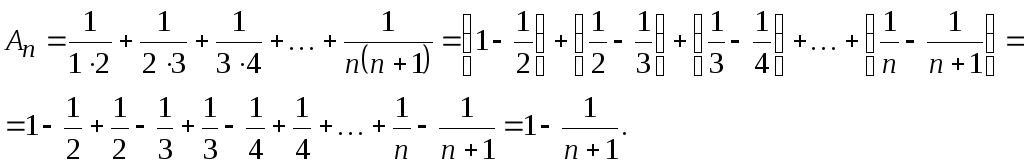
Эта
сумма при
![]() имеет предел
имеет предел
![]() .
.
Итак, данный ряд сходится и его сумма равна единице.
Основные свойства сходящихся рядов
Если ряд
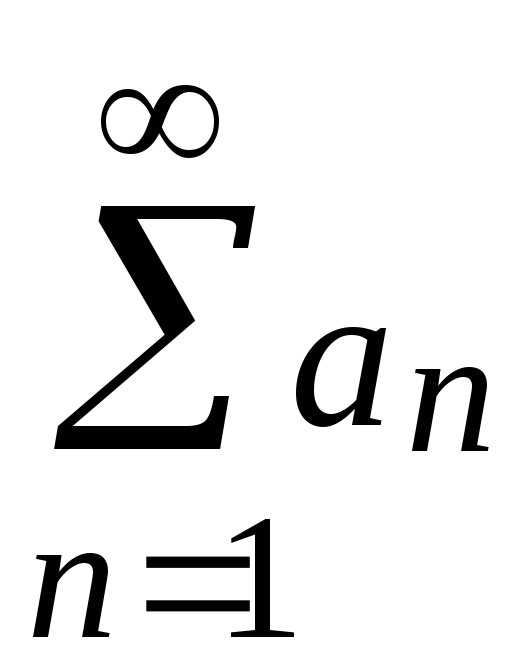 сходится,
то сходится и ряд, полученный отбрасыванием
из него любого конечного числа членов.
сходится,
то сходится и ряд, полученный отбрасыванием
из него любого конечного числа членов.Пусть даны ряды
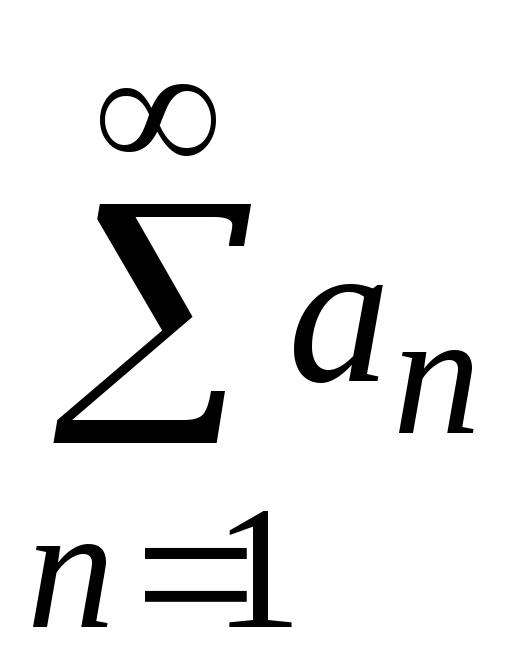 ,
,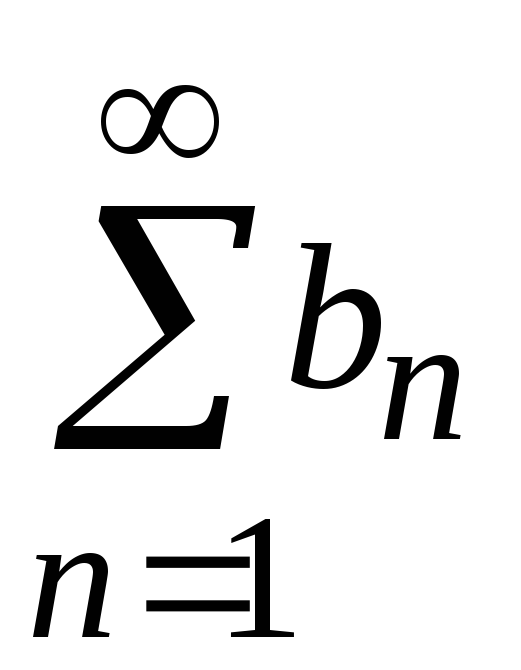 и
и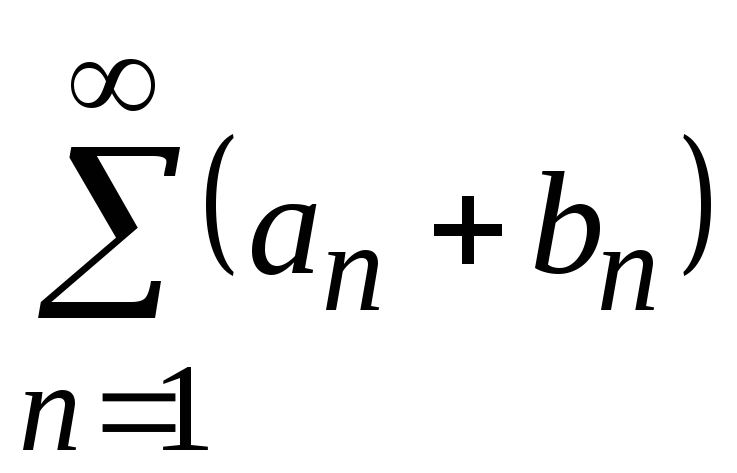 .
Если оба ряда
.
Если оба ряда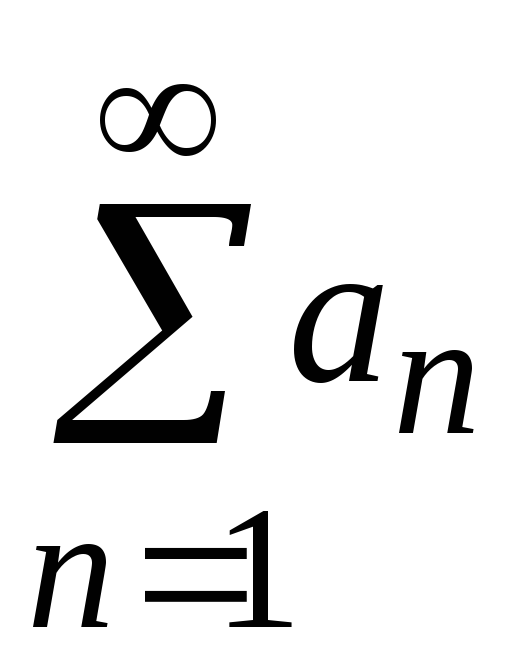 и
и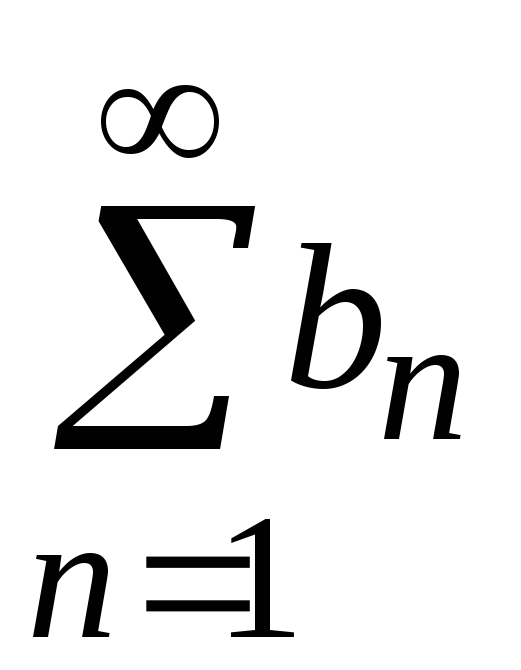 сходятся, а их суммы соответственно
равны
сходятся, а их суммы соответственно
равны и
и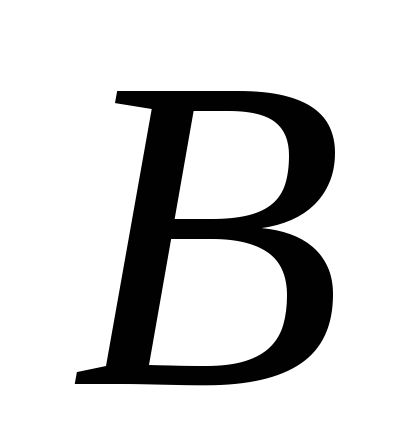 ,
то сходится и ряд
,
то сходится и ряд
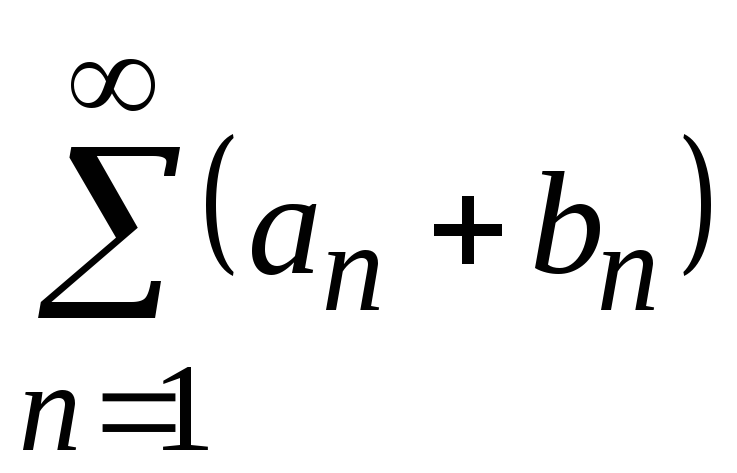 ,
причем его сумма равна
,
причем его сумма равна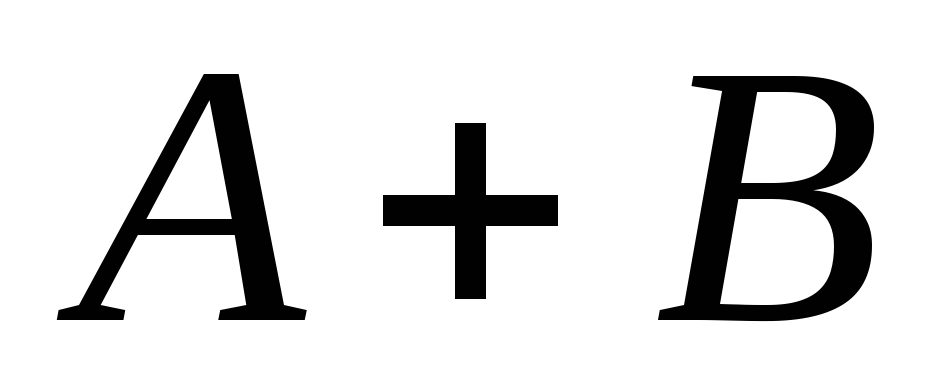 .
.Если ряд
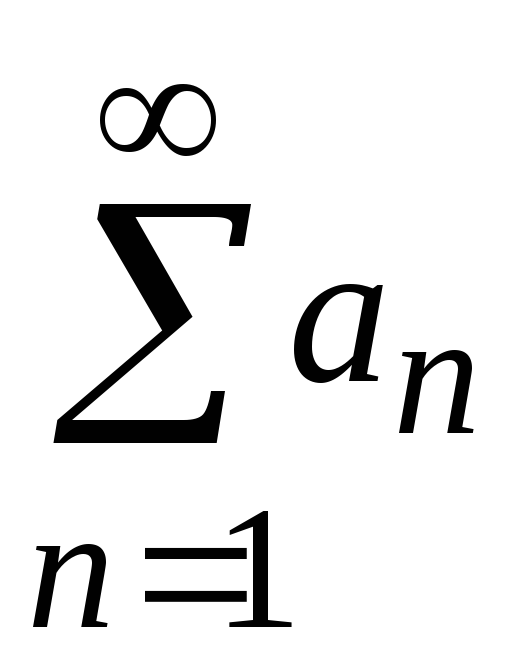 сходится и имеет сумму
сходится и имеет сумму ,
то сходится и ряд
,
то сходится и ряд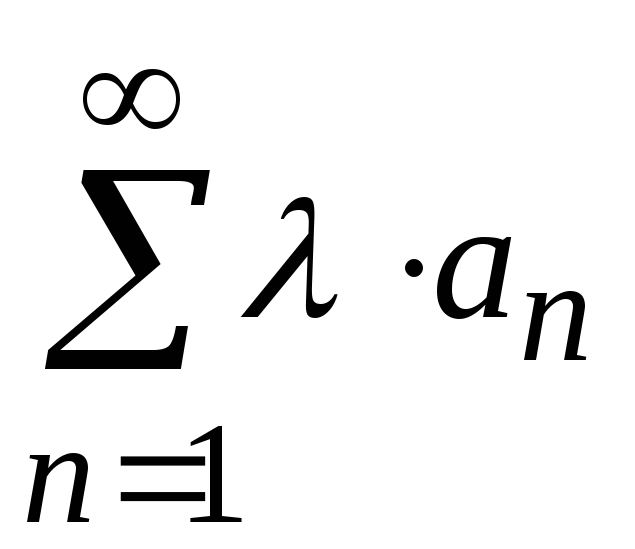 ,
причем его сумма равна числу
,
причем его сумма равна числу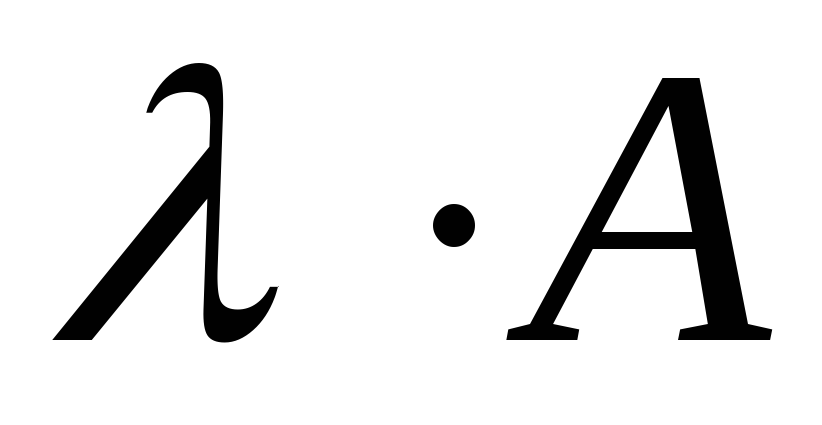 ,
где
,
где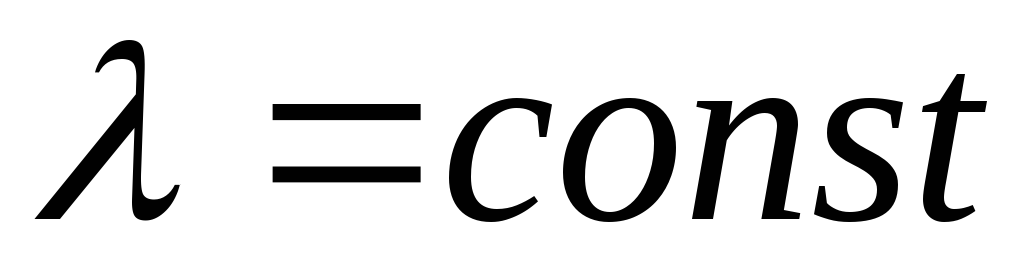 .
.Если ряд
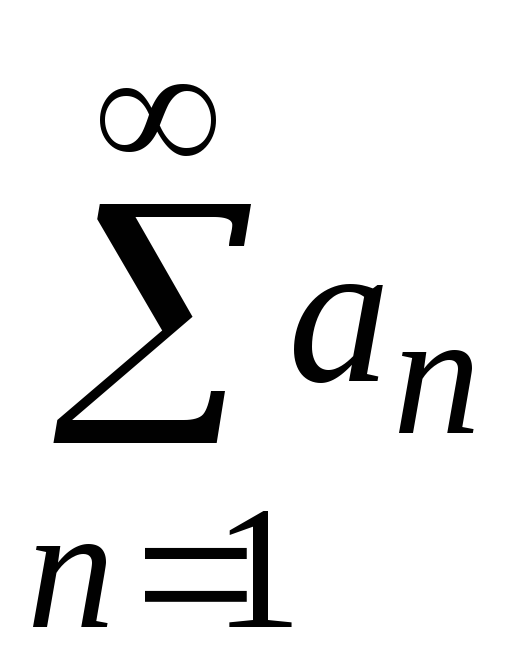 сходится, то сходится и любой ряд,
полученный из него группировкой
слагаемых, не изменяющей порядок
расположения членов ряда, и суммы этих
рядов одинаковы. К примеру, если
сходится, то сходится и любой ряд,
полученный из него группировкой
слагаемых, не изменяющей порядок
расположения членов ряда, и суммы этих
рядов одинаковы. К примеру, если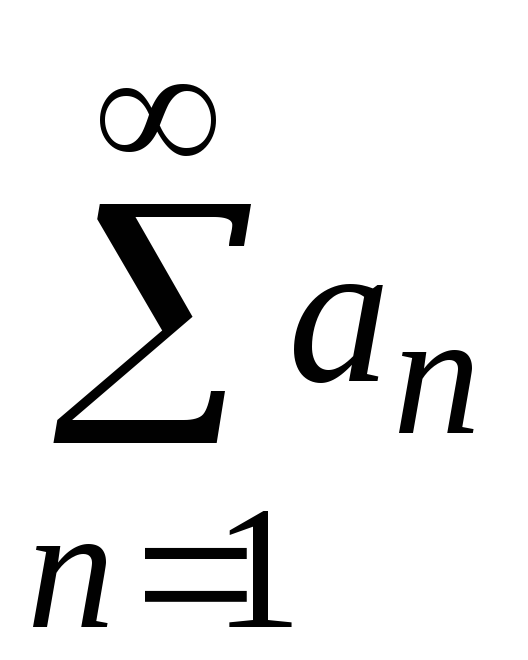 сходится и его сумма равна
сходится и его сумма равна ,
то ряд
,
то ряд
![]()
также
сходится, и его сумма равна
![]() .
.
Эти свойства доказываются с помощью определения сходящихся рядов. Для примера докажем второе свойство.
Пусть ![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
Очевидно,
что при любом
![]()
![]() .
Тогда
.
Тогда![]() ,
что доказывает рассматриваемое свойство.
- данный знак означает окончание
доказательства теорем.
,
что доказывает рассматриваемое свойство.
- данный знак означает окончание
доказательства теорем.
