3.2. Задача об оптимальной стратегии замены оборудования

Известно, что оборудование со временем изнашивается, стареет физически и морально. В процессе эксплуатации падает производительность, и растут эксплуатационные расходы на текущий ремонт. Со временем возникает необходимость замены оборудования, так как его дальнейшая эксплуатация обходится дороже, чем замена. Отсюда задача о замене оборудования может быть сформулирована следующим образом.

Разработать оптимальную стратегию замены оборудования возраста лет в плановом периоде продолжительностьюлет, если известны:

– стоимость продукции, производимой в течение года на оборудовании возрасталет ();

– ежегодные расходы, связанные с эксплуатацией оборудования возрасталет ();

– остаточная стоимость оборудования возрасталет;

– стоимость нового оборудования и расходы, связанные с его установкой, наладкой и запуском.

Поставленную задачу нужно рассмотреть как многошаговую.

На этапе условной оптимизации будем находить максимальную прибыль за последний год планового периода эксплуатации оборудования возраста t лет, за два последних года, за три последних года и т.д., и наконец, за весь плановый период.

В начале каждого года имеется две возможности – сохранить оборудование и получить прибыль или заменить его и получить прибыль. Прибыль от использования оборудования в последнем-м году планового периода запишется в следующем виде

(3.4)

а прибыль от использования оборудования в период с -го по-й год

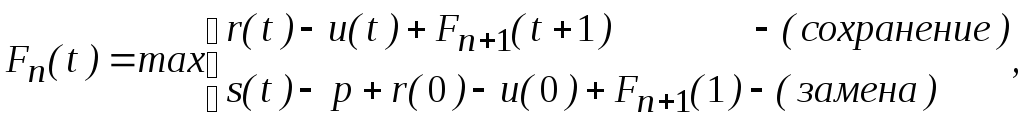(3.5)

где – прибыль от использования оборудования в период с-го по-й год.

В случае, если оба управления («сохранение» и «замена») приводят к одной и той же прибыли, то целесообразно выбрать управление «сохранение».

На этапе безусловной оптимизации определяется оптимальная стратегия замены оборудования на протяжении всего планового периода.

Пример 3.2

Найти оптимальную стратегию замены оборудования возраста 3 года на период продолжительностью 10 лет, если для каждого года планового периода известны стоимость продукции, производимой с использованием этого оборудования, и эксплуатационные расходы(табл. 3.6). Известны также остаточная стоимость, не зависящая от возраста оборудования и составляющая 4 ден. ед., и стоимость нового оборудования, равная 18 ден. ед., не меняющаяся в плановом периоде.

Таблица 3.6

	0	1	2	3	4	5	6	7	8	9	10
	31	30	28	28	27	26	26	25	24	24	23
	8	9	9	10	10	10	11	12	14	16	18

Решение

I этап. Условная оптимизация.

1-й шаг. . Начнем процедуру условной оптимизации с последнего, десятого года планового периода. Найдем максимальную прибыль, получаемую от оборудования возрастаt () лет за последний год планового периода. Функциональное уравнение (3.4) с учетом числовых данных примера принимает вид

.

Тогда

;

;

;

;

;

;

;

;

;

;

.

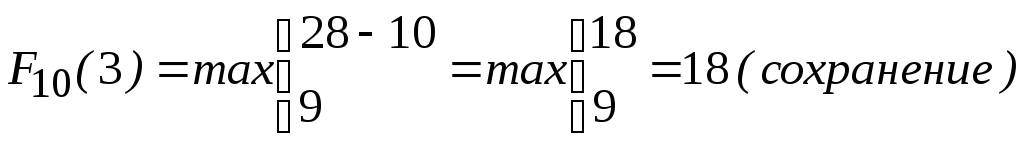Полученные результаты занесём в таблицу (первая строка табл. 3.7).

2-й шаг. . Найдем максимальную прибыль, получаемую от оборудования возрастаt () лет за последние два года (9-ый и 10-ый) планового периода. Функциональное уравнение (3.5) с учетом числовых данных примера принимает вид

.

Тогда

;

;

;

;

;

;

.

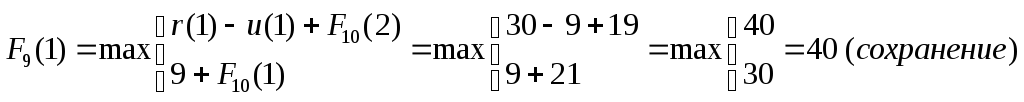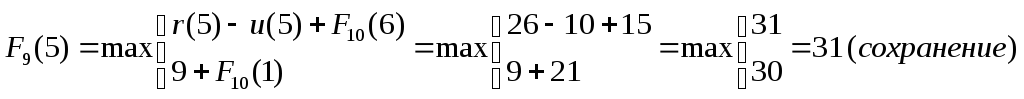Т.к. оборудование возраста 6 лет следует заменить, то и на более старом оборудовании работать будет не целесообразно, т.е. можно сразу записать .

Полученные результаты занесём в таблицу (вторая строка табл. 3.7).

3-й шаг. . Найдем максимальную прибыль, получаемую от оборудования возрастаt () лет за последние три года (с 8-го по 10-ый) планового периода. Функциональное уравнение (3.5) с учетом числовых данных примера принимает вид

.

Тогда

;

;

;

;

;

Т.к. оборудование возраста 4 года следует заменить, то и на более старом оборудовании работать будет не целесообразно, т.е. можно сразу записать .

Полученные результаты занесём в таблицу (третья строка табл. 3.7).

4-й шаг. . Найдем максимальную прибыль, получаемую от оборудования возрастаt () лет за последние четыре года (с 7-го по 10-ый) планового периода. Функциональное уравнение (3.5) с учетом числовых данных примера принимает вид

.

Тогда

;

;

;

.

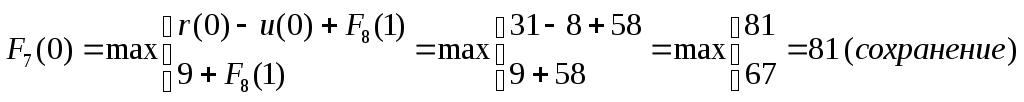Здесь оба управления («сохранение» и «замена») приводят к одной и той же прибыли, то целесообразно выбрать управление «сохранение».

;

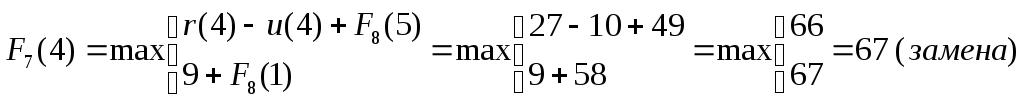Т.к. оборудование возраста 4 года следует заменить, то и на более старом оборудовании работать будет не целесообразно, т.е. можно сразу записать .

Полученные результаты занесём в таблицу (четвертая строка табл. 3.7).

Продолжая вычисления описанным способом, постепенно заполняем всю таблицу (табл. 3.7). При этом области «сохранения» и «замены» разделим жирной линией (табл. 3.7).

Таблица 3.7

	0	1	2	3	4	5	6	7	8	9	10
	23	21	19	18	17	16	15	13	10	9	9
	44	40	37	35	33	31	30	30	30	30	30
	63	58	54	51	49	49	49	49	49	49	49
	81	75	70	67	67	67	67	67	67	67	67
	98	91	86	85	84	84	84	84	84	84	84
	114	107	104	102	101	100	100	100	100	100	100
	130	125	121	119	117	116	116	116	116	116	116
	148	142	138	135	134	134	134	134	134	134	134
	165	159	154	152	151	151	151	151	151	151	151
	182	175	171	169	168	168	168	168	168	168	168

Итак, максимальную прибыль, получаемую от оборудования возраста 3 года за весь плановый период ден. ед.