Проверка на оптимальность невырожденного опорного плана методом потенциалов

1) Каждому поставщику поставим в соответствие потенциал , а каждому потребителю потенциал.

Тогда каждой занятой клетке будет соответствовать уравнение:

.

Так как всех занятых клеток должно быть m+n–1, то есть на единицу меньше числа потенциалов, то для нахождения необходимо решить систему изm+n–1 уравнений сm+n неизвестными. Система является линейно-зависимой и, чтобы найти частное решение, одному из потенциалов нужно присвоить произвольное числовое значение, тогда остальные потенциалы определяются однозначно. Для исследования плана на оптимальность для каждой свободной клетки считаем оценки по формуле:

;

а) если все оценки положительны, то найденный опорный план оптимален и единственен ;

б) если наряду с положительными оценками встречаются и нулевые оценки , то найденный опорный план оптимален, но не единственен;

в) если оценка хотя бы одной свободной клетки отрицательна , то опорный план не является оптимальным, его можно улучшить за счет загрузки этой клетки. Если таких клеток несколько, то наиболее перспективной для загрузки является клетка с наименьшей оценкой. Например, для клетокимеем оценки. Здесь наиболее перспективной для загрузки является клетка.

Переход к новому опорному плану

План перевозок можно улучшить за счет загрузки свободной клетки с отрицательной оценкой. Для этого для наиболее перспективной для загрузки свободной клетки строится замкнутый цикл с вершинами в загруженных клетках. Вершинам этого цикла условно присваиваются знаки: свободной клетке – плюс, следующей по (или против) часовой стрелке занятой клетке – минус, следующей – снова плюс и т.д. Из значений в клетках цикла помеченных знаком минус выбирается наименьшее количество груза, которое прибавляется к значениям клеток, помеченных знаком плюс и отнимается от значений, помеченных знаком минус.

Цикл пересчета

В общем случае цикл пересчета представляет собой замкнутую ломаную линию, состоящую из звеньев, пересекающихся под прямым углом. Каждое звено соединяет две клетки одной линии (строки или столбца). В цикле всегда четное число клеток, причем только одна свободная, та относительно которой он составлен, остальные клетки цикла загружены. Для любой свободной клетки всегда можно построить единственный цикл.

Пример 2.5

По данным примера 2.1 исходя из начального опорного плана найденного в примере 2.2 решить транспортную задачу (найти оптимальный план перевозок и минимальные затраты на транспортировку всего топлива).

Решение

Воспользуемся распределительной таблицей, в которой найден начальный опорный план методом «минимального элемента» (табл. 2.4 и табл. 2.7).

Таблица 2.7

	Потребители										Запас топлива, т
Хранилища
		5		4		3		6		0	70
	40		20						10
		4		3		5		1		0	90
			50				40
		2		4		1		5		0	50
	10				40
Потребность в топливе, т	50		70		40		40		10		210

Для проверки найденного плана на оптимальность найдем потенциалы строк и столбцов (табл. 2.7), составив для каждой занятой клетки уравнение . При этом получим следующую систему уравнений:

Система является линейно-зависимой, для нахождения одного из частных решений присвоим одному из потенциалов любое числовое значение, например , и найдем значения остальных потенциалов:

Потенциалы можно находить непосредственно в распределительной таблице. Нужно присвоить какому-нибудь потенциалу любое числовое значение и по цепочке, используя уравнение , по занятым клеткам найти все остальные потенциалы (в табл. 2.8 указана очередность нахождения потенциалов, приняв).

Таблица 2.8

	Потребители										Запас топлива, т
Хранилища
		5		4		3		6		0	70	1)
	40	–	20			+			10
		4		3		5		1		0	90	6)
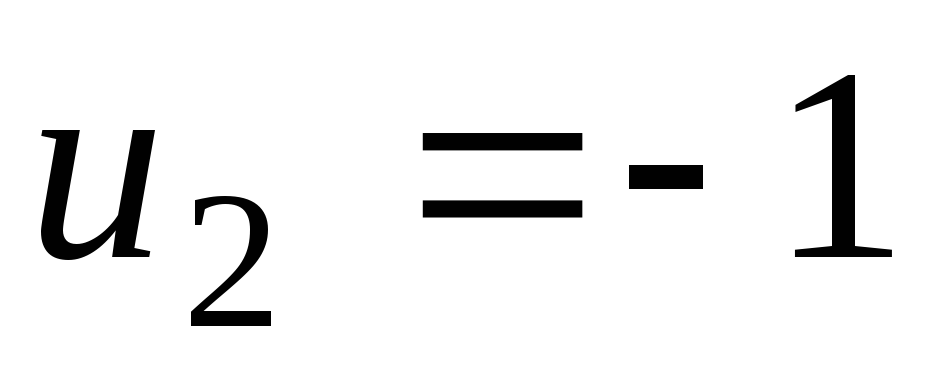
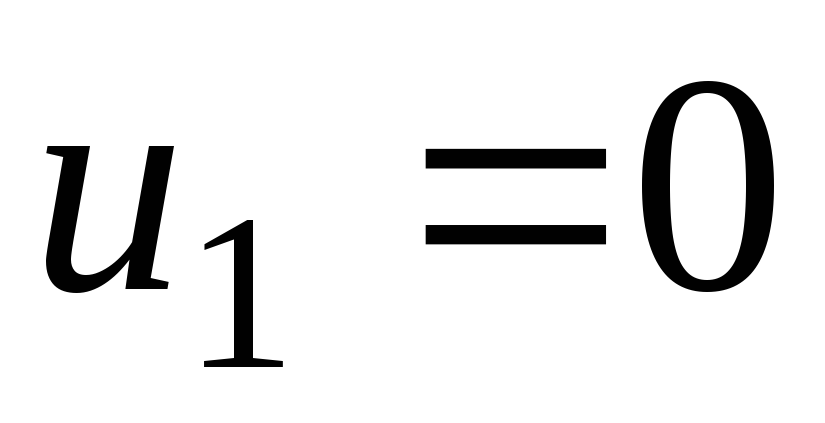
			50				40
		2		4		1		5		0	50	5)
	10	+			40	–
Потребность в топливе, т	50		70		40		40		10		210
	2)		3)		7)		8)		4)

Оценки свободных клеток найдем по формуле :

Так как среди оценок есть отрицательная (), то найденный план не оптимален. Его можно улучшить путем загрузки этой клетки.

Составим цикл пересчета относительно клетки (1,3) и присвоим клеткам цикла знаки «+» и «–». Свободной клетке (1,3) присвоим знак «+», а дальше, по часовой стрелке, следующей клетке цикла (3,3) присвоим знак «–», затем клетке цикла (3,1) присвоим знак «+», далее клетке цикла (1,1) присвоим знак «–» (табл. 2.8).

Из клеток, помеченных знаком «–», выбираем наименьшее количество груза . Чтобы получить новый опорный план нужно прибавить значениек поставкам в клетках, помеченных знаком «+» и вычесть из поставок в клетках, помеченных знаком «–», нули при этом не записываются (табл. 2.9). Т.к. значениеоказалось в двух клетках цикла (клети (1,1) и (3,3) табл. 2.8), то чтобы новый опорный план оказался невырожденным необходимо в одной из этих клеток поставить базисный ноль и считать ее занятой (табл. 2.9).

Таблица 2.9

	Потребители										Запас топлива, т
Хранилища
		5		4		3		6		0	70
	0		20		40				10
		4		3		5		1		0	90
			50				40
		2		4		1		5		0	50
	50
Потребность в топливе, т	50		70		40		40		10		210

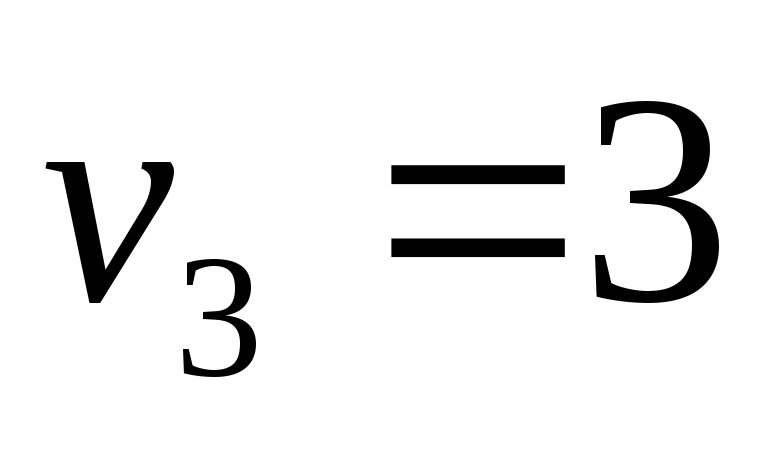
Проверим найденный план на оптимальность. Потенциалы строк и столбцов найдены непосредственно в распределительной таблице (табл. 2.9).

Найдем оценки свободных клеток:

Т.к. все оценки неотрицательны, то найденный опорный план является оптимальным, а т.к. есть нулевая оценка (), то не единственен.

Итак, получен оптимальный план:

.

Транспортные издержки для этого плана:

(усл. ден. ед.).

Итак, по оптимальному плану, необходимо из хранилища А₁ потребителю B₂ доставить 20 т топлива, потребителю B₃  – 40 т топлива; из хранилища А₂ потребителю В₂ доставить 50 т топлива, а потребителю В₄ – 40 т топлива; из хранилища А₃ доставить 50 т топлива потребителю В₁.

При этом затраты на транспортировку будут минимальными и составят 490 усл. ден. ед. Нераспределенное топливо, в размере 10 т останется в хранилище А₁.

Пример 2.6

В четырех хранилищах имеется соответственно 100, 50, 120 и 80 т картофеля. Требуется так спланировать перевозки картофеля к пяти овощным магазинамспрос которых равен соответственно 20, 120, 180, 30 и 100 т, чтобы суммарные транспортные издержки были минимальными. Известны стоимости перевозок 1 т картофеля (ден. ед.) из-го () хранилища в-й () магазин.

Требуется: а) составить математическую модель задачи; б) найти оптимальный план перевозок и минимальные транспортные издержки (решить задачу методом потенциалов исходя из начального опорного плана найденного методом «северо-западного угла»).

Решение

Т.к для данной задачи выполняется условие , то задача является несбалансированной. Преобразуем модель к сбалансированному виду. Добавим поставщика (хранилище), запас которого равен:

(20+120+180+30+100) – (100+50+120+80)=100.

Тарифы фиктивного поставщика равны нулю, т.е. .

Матричная модель сбалансированной задачи будет иметь вид:

	Магазины										Запас, т
Хранилища	В1		В2		В3		В4		В5
А1		5		3		8		2		1	100
А2		10		4		6		7		2	50
А3		3		5		8		4		7	120
А4		10		3		7		8		6	80
А5		0		0		0		0		0	100
Спрос, т	20		120		180		30		100		450

а) составить математическую модель задачи.

Введем переменные – количество картофеля, которое необходимо доставить из-го хранилища в-й магазин.

Целевая функция (затраты на перевозку всего картофеля) будет иметь вид:

Система ограничений задачи:

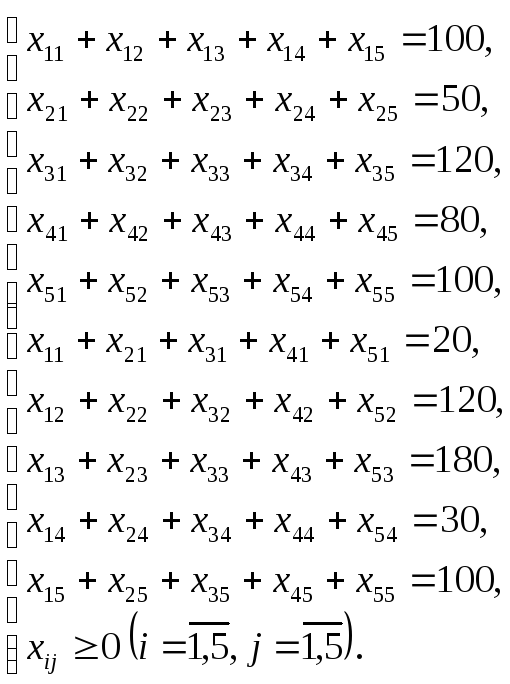
б) Найдем начальный опорный план методом «северо-западного угла» (табл. 2.10).

Таблица 2.10

	Магазины										Запас, т
Хранилища	В1		В2		В3		В4		В5
А1		5		3		8		2		1	100	=0
	20		80
А2		10		4		6		7		2	50	=1
			40		10
А3		3		5		8		4		7	120	=3
					120
А4		10		3		7		8		6	80	=2
					50		30
А5		0		0		0		0		0	100	=–6
							0		100
Спрос, т	20		120		180		30		100		450
	=5		=3		=5		=6		=6

Для проверки плана на оптимальность каждому поставщику поставим в соответствие потенциал , а каждому потребителю потенциал. Найдем их значения непосредственно в распределительной таблице. Для этого присвоим потенциалу и найдем значения остальных потенциалов, используя уравнения для занятых клеток (табл. 2.10).

Для исследования плана на оптимальность для каждой свободной клетки считаем оценки по формуле :

Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки с наименьшей отрицательной оценкой, т.к. таких клеток несколько (клетки (1,5), (2,5), (3,1), (3,4)), то возьмем любую из них, например клетку (1,5). Составим цикл пересчета относительно этой клетки (табл. 2.11).

Таблица 2.11

	Магазины										Запас, т
Хранилища	В1		В2		В3		В4		В5
А1		5		3		8		2		1	100	=0
	20		80	–						+
А2		10		4		6		7		2	50	=1
			40	+	10	–
А3		3		5		8		4		7	120	=3
					120
А4		10		3		7		8		6	80	=2
					50	+	30	–
А5		0		0		0		0		0	100	=–6
							0	+	100	–
Спрос, т	20		120		180		30		100		450
	=5		=3		=5		=6		=6

Из клеток, помеченных знаком «–» выбираем наименьшее количество груза . Прибавляем значениек поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», получим новый план перевозок (табл. 2.12).

Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.12).

Таблица 2.12

	Магазины										Запас, т
Хранилища	В1		В2		В3		В4		В5
А1		5		3		8		2		1	100	=0
	20	–	70						10	+
А2		10		4		6		7		2	50	=1
			50
А3		3		5		8		4		7	120	=8
		+			120	–
А4		10		3		7		8		6	80	=7
					60	+	20	–
А5		0		0		0		0		0	100	=–1
							10	+	90	–
Спрос, т	20		120		180		30		100		450
	=5		=3		=0		=1		=1

Оценки свободных клеток:

Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (3,1). Составим цикл пересчета относительно этой клетки (табл. 2.12). Из клеток, помеченных знаком «–» выбираем наименьшее количество груза . Прибавляем значениек поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», при этом в одну из клеток, которые имеют поставки (это клетки (1,1) и (4,4)) нужно поставить ноль и считать ее занятой, например в клетку (1,1). Таким образом, получим новый невырожденный план перевозок (табл. 2.13).

Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.13).

Таблица 2.13

	Магазины										Запас, т
Хранилища	В1		В2		В3		В4		В5
А1		5		3		8		2		1	100	=0
	0	–	70						30	+
А2		10		4		6		7		2	50	=1
			50
А3		3		5		8		4		7	120	=–2
	20	+			100	–
А4		10		3		7		8		6	80	=–3
					80
А5		0		0		0		0		0	100	=–1
						+	30		70	–
Спрос, т	20		120		180		30		100		450
	=5		=3		=10		=1		=1

Оценки свободных клеток:

Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (5,3). Составим цикл пересчета относительно этой клетки (табл. 2.13). Из клеток, помеченных знаком «–» выбираем наименьшее количество груза . Прибавляя значениек поставкам в клетках, помеченных знаком «+» и вычитая из поставок в клетках, помеченных знаком «–», значения в клетках не изменятся, но в новом плане клетка (5,3) станет базисной (заполнена нулем), а клетка (1,1) станет свободной. Таким образом, получим новый невырожденный план перевозок (табл. 2.14).

Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.14).

Таблица 2.14

	Магазины										Запас, т
Хранилища	В1		В2		В3		В4		В5
А1		5		3		8		2		1	100	=0
			70	–					30	+
А2		10		4		6		7		2	50	=1
			50
А3		3		5		8		4		7	120	=7
	20				100
А4		10		3		7		8		6	80	=6
				+	80	–
А5		0		0		0		0		0	100	=–1
					0	+	30		70	–
Спрос, т	20		120		180		30		100		450
	=–4		=3		=1		=1		=1

Оценки свободных клеток:

Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (4,2). Составим цикл пересчета относительно этой клетки (табл. 2.14). Из клеток, помеченных знаком «–» выбираем наименьшее количество груза . Прибавляем значениек поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», при этом в одну из клеток, которые имеют поставки (это клетки (1,2) и (5,5)) нужно поставить ноль и считать ее занятой, например в клетку (5,5). Таким образом, получим новый невырожденный план перевозок (табл. 2.15).

Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.15).

Таблица 2.15

	Магазины										Запас, т
Хранилища	В1		В2		В3		В4		В5
А1		5		3		8		2		1	100	=0
									100
А2		10		4		6		7		2	50	=7
			50	–						+
А3		3		5		8		4		7	120	=7
	20				100
А4		10		3		7		8		6	80	=6
			70	+	10	–
А5		0		0		0		0		0	100	=–1
					70	+	30		0	–
Спрос, т	20		120		180		30		100		450
	=–4		=–3		=1		=1		=1

Оценки свободных клеток:

Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (2,5). Составим цикл пересчета относительно этой клетки (табл. 2.15). Из клеток, помеченных знаком «–» выбираем наименьшее количество груза . Прибавляя значениек поставкам в клетках, помеченных знаком «+» и вычитая из поставок в клетках, помеченных знаком «–», значения в клетках не изменятся, но в новом плане клетка (2,5) станет базисной (заполнена нулем), а клетка (5,5) станет свободной. Таким образом, получим новый невырожденный план перевозок (табл. 2.16).

Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.16).

Таблица 2.16

	Магазины										Запас, т
Хранилища	В1		В2		В3		В4		В5
А1		5		3		8		2		1	100	=0
								+	100	–
А2		10		4		6		7		2	50	=1
			50	–					0	+
А3		3		5		8		4		7	120	=1
	20				100
А4		10		3		7		8		6	80	=0
			70	+	10	–
А5		0		0		0		0		0	100	=–7
					70	+	30	–
Спрос, т	20		120		180		30		100		450
	=2		=3		=7		=7		=1

Оценки свободных клеток:

Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (1,4). Составим цикл пересчета относительно этой клетки (табл. 2.16), при этом клетка (2,4), в которой звенья цикла пересекаются, не участвует в цикле. Из клеток, помеченных знаком «–» выбираем наименьшее количество груза . Прибавляем значениек поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», получим новый план перевозок (табл. 2.17).

Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.17).

Таблица 2.17

	Магазины										Запас, т
Хранилища	В1		В2		В3		В4		В5
А1		5		3		8		2		1	100	=0
							10	+	90	–
А2		10		4		6		7		2	50	=1
			40	–					10	+
А3		3		5		8		4		7	120	=6
	20			+	100	–
А4		10		3		7		8		6	80	=0
			80
А5		0		0		0		0		0	100	=–2
					80	+	20	–
Спрос, т	20		120		180		30		100		450
	=–3		=3		=2		=2		=1

Оценки свободных клеток:

Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки с наименьшей отрицательной оценкой, т.к. таких две клетки ((3,2) и (3,4)), то возьмем любую из них, например клетку (3,2). Составим цикл пересчета относительно этой клетки (табл. 2.17), при этом клетка (2,4), в которой звенья цикла пересекаются, не участвует в цикле. Из клеток, помеченных знаком «–» выбираем наименьшее количество груза . Прибавляем значениек поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», получим новый план перевозок (табл. 2.18).

Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.18).

Таблица 2.18

	Магазины										Запас, т
Хранилища	В1		В2		В3		В4		В5
А1		5		3		8		2		1	100	=0
							30		70
А2		10		4		6		7		2	50	=1
			20	–		+			30
А3		3		5		8		4		7	120	=2
	20		20	+	80	–
А4		10		3		7		8		6	80	=0
			80
А5		0		0		0		0		0	100	=–6
					100
Спрос, т	20		120		180		30		100		450
	=1		=3		=6		=2		=1

Оценки свободных клеток:

Так как среди оценок есть отрицательная, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (2,3) с отрицательной оценкой. Составим цикл пересчета относительно этой клетки (табл. 2.18). Из клеток, помеченных знаком «–» выбираем наименьшее количество груза . Прибавляем значениек поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», получим новый план перевозок (табл. 2.19).

Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.19).

Таблица 2.19

	Магазины										Запас, т
Хранилища	В1		В2		В3		В4		В5
А1		5		3		8		2		1	100	=0
							30	–	70	+
А2		10		4		6		7		2	50	=1
					20	+			30	–
А3		3		5		8		4		7	120	=3
	20		40		60	–		+
А4		10		3		7		8		6	80	=1
			80
А5		0		0		0		0		0	100	=–5
					100
Спрос, т	20		120		180		30		100		450
	=0		=2		=5		=2		=1

Оценки свободных клеток:

Так как среди оценок есть отрицательная, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (3,4) с отрицательной оценкой. Составим цикл пересчета относительно этой клетки (табл. 2.19), при этом клетка (2,4), в которой звенья цикла пересекаются, не участвует в цикле. Из клеток, помеченных знаком «–» выбираем наименьшее количество груза . Прибавляем значениек поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», при этом в одну из клеток, которые имеют поставки (это клетки (1,4) и (2,5)) нужно поставить ноль и считать ее занятой, например в клетку (2,5). Таким образом, получим новый невырожденный план перевозок (табл. 2.20).

Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.20).

Таблица 2.20

	Магазины										Запас, т
Хранилища	В1		В2		В3		В4		В5
А1		5		3		8		2		1	100	=0
									100
А2		10		4		6		7		2	50	=1
					50				0
А3		3		5		8		4		7	120	=3
	20		40		30		30
А4		10		3		7		8		6	80	=1
			80
А5		0		0		0		0		0	100	=–5
					100
Спрос, т	20		120		180		30		100		450
	=0		=2		=5		=1		=1

Оценки свободных клеток:

Так как все оценки положительные, то найденный опорный план является оптимальным и единственным.

Итак, получили оптимальный план:

.

Транспортные издержки для этого плана:

(ден. ед.).

Итак, по оптимальному плану, необходимо из хранилища А₁ магазину B₅ доставить 100 т картофеля; из хранилища А₂ магазину В₃ доставить 50 т картофеля; из хранилища А₃ доставить 20 т магазину В₁, 40 т магазину В₂, 30 т магазину В₃ и 30 т картофеля магазину В₄; из хранилища А₄ доставить 80 т картофеля магазину В₂; при этом спрос магазина В₃ останется неудовлетворенным на 100 т картофеля. При этом затраты на транспортировку будут минимальными и составят 1260 ден. ед.

Задачи

2.1 – 2.8 Транспортная задача, представлена распределительной таблицей. Тарифы перевозок, спрос потребителей и запасы поставщиков указаны в таблице.

а) Составить математическую модель задачи;

б) Найти начальный опорный план методом «северо-западного угла», оптимальный план перевозок и соответствующие ему затраты по перевозки груза.

в) Найти начальный опорный план методом Фогеля, оптимальный план перевозок и соответствующие ему затраты по перевозки груза.

г) Найти начальный опорный план методом «минимального элемента», оптимальный план перевозок и соответствующие ему затраты по перевозки груза.

2.1

	Потребители				Запасы
Поставщики	В1	В2	В3	В4	груза,
А1	4	5	7	1	40
А2	9	6	3	2	70
А3	6	5	2	4	60
А4	2	4	5	3	50
Спрос,	85	50	75	25

2.2

	Потребители				Запасы
Поставщики	В1	В2	В3	В4	груза,
А1	3	4	5	6	80
А2	9	6	3	7	70
А3	6	5	2	4	50
Спрос,	45	40	55	20

2.3

	Потребители			Запасы
Поставщики	В1	В2	В3	груза,
А1	5	4	9	140
А2	3	6	1	150
А3	4	8	6	130
А4	2	5	4	70
Спрос,	100	250	130

2.4

	Потребители			Запасы
Поставщики	В1	В2	В3		груза,
А1	1	4	3		40
А2	5	3	4		50
А3	6	8	7		20
А4	4	6	9		70
А5	6	4	2		40
Спрос,	80	90	75

2.5

	Потребители				Запасы
Поставщики	В1	В2	В3	В4	груза,
А1	5	3	4	6	20
А2	9	7	2	8	35
А3	2	4	1	5	15
Спрос,	10	15	20	10

2.6

	Потребители				Запасы
Поставщики	В1	В2	В3	В4	груза,
А1	7	5	6	1	50
А2	3	1	4	3	80
А3	6	7	9	8	40
А4	2	6	3	4	30
Спрос,	70	50	20	40

2.7

	Потребители				Запасы
Поставщики	В1	В2	В3	В4	груза,
А1	5	7	4	9	250
А2	3	1	6	5	350
Спрос,	150	200	100	250

2.8

	Потребители					Запасы
Поставщики	В1	В2	В3	В4	В5	груза,
А1	3	6	7	2	9	60
А2	5	2	5	4	8	30
А3	8	4	3	5	2	90
Спрос,	20	40	30	10	15

2.9

Четыре магазина получают овощи из трех совхозовкоторые ежедневно могут поставлять соответственно 15, 16 и 24 т. Суточные потребности магазинов составляют 12, 14, 16 и 15 т. Известна матрица транспортных расходов на доставку 1 т овощей из совхоза магазину:

.

Найти оптимальный план доставки овощей из совхозов магазинам и минимальные транспортные издержки на перевозку всех овощей.

2.10

На пять строительных площадок поступает кирпич с трех заводов. Ежедневная потребность в кирпиче на строительных площадках равна соответственно: 50, 65, 45, 40 и 60 тыс. шт. Данные о производительности заводов за день и транспортные расходы на 1 тыс. шт. приведены в таблице:

	Транспортные расходы на 1 тыс. шт. по строительным площадкам, ден. ед.					Производитель-ность заводов за день, тыс. шт.
Заводы	В1	В2	В3	В4	В5
А1	5	3	4	2	5	90
А2	9	6	7	5	3	110
А3	2	4	8	1	4	80

Определить оптимальный план закрепления строительных площадок за кирпичными заводами, чтобы затраты на транспортировку кирпича были минимальными.

2.11

На заводах №1, №2 и №3 производится однородная продукция в количестве 70, 80 и 60 единиц. При этом затраты на производство единицы продукции на заводах составляют соответственно 3, 2 и 4 ден.ед. Четырем потребителям требуется соответственно 40, 65, 55 и 60 единиц продукции. Расходы (ден. ед.) по перевозке единицы продукции с-го завода-му потребителю известны.

.

Для полного удовлетворения потребностей необходимо увеличить выпуск продукции на первом заводе. При этом дополнительные затраты на производство единицы дополнительной продукции равны 1 ден.ед.

Требуется найти оптимальный план доставки продукции потребителю, при котором совокупные затраты, связанные с изготовлением продукции и ее доставкой потребителям будут минимальными.

2.12

Составить план посева зерновых культур (с учетом плодородия почвы), при котором урожай будет максимальным. Площадь I участка равна 200 га, участка II – 150 га, участка III – 250 га, участка IV – 100 га. Все необходимые данные приведены в таблице:

Зерновые культуры	Урожайность по участкам, ц/га				Посевные
	I	II	III	IV	площади, га
Рожь	30	25	28	26	180
Пшеница	40	37	35	38	350
Ячмень	35	32	29	34	170