35.. Оптимальный прием дискретных сообщений с неопределенной фазой (Некогерентный прием).

В тех случаях, когда не удаётся точно оценить фазу или эта оценка требует применения сложных устройств, используют алгоритм, построенный в предположении, что начальная фаза приходящего сигнала неизвестна и может принимать любое значение на интервале . Такой метод приёма называется некогерентным. Для вывода правила оптимального некогерентного приёма воспользуемся критерием максимального правдоподобия. Математическая модель такого канала:

(13.1)

где – преобразование Гильберта отu(t), – случайная начальная фаза,k– коэффициент передачи канала.

Введём обозначения:

(13.2)

_(13.3)

(13.4)

(13.5)

(13.6)

Тогда можно записать:

, (13.7)

где - модифицированная функция Бесселя. (13.8)

Вместо того, чтобы сравнить отношения правдоподобия можно сравнить их логарифмы, что приводит к следующему алгоритму, который для двоичной системы будет выглядеть:

(13.9)

При выполнении этого неравенства регистрируется 1, в противном случае – 0. Величины иможно получить в момент отсчёта Т на выходе активного фильтра с опорными сигналами, равными соответственно и С учётом сказанного можно осуществить построение на основе активных фильтров схемы, называемой квадратурной и реализующей алгоритм (13.9).

Здесь –соответственно генераторы опорных сигналов ; 90 градусов – фазовращатель всех сигнальных компонентов на 90 градусов (преобразователь Гильберта); БОМ – блок определения модуля вектора; НУ – нелинейные безынерционные устройства с характеристикой.(13.10)

Величины не зависят от начальной фазы сигналови пропорциональны огибающей (в моменты отсчёта, кратные Т) на выходе фильтра, согласованного с сигналом. Таким образом, алгоритм (13.9) можно реализовать и на базе согласованных фильтров.

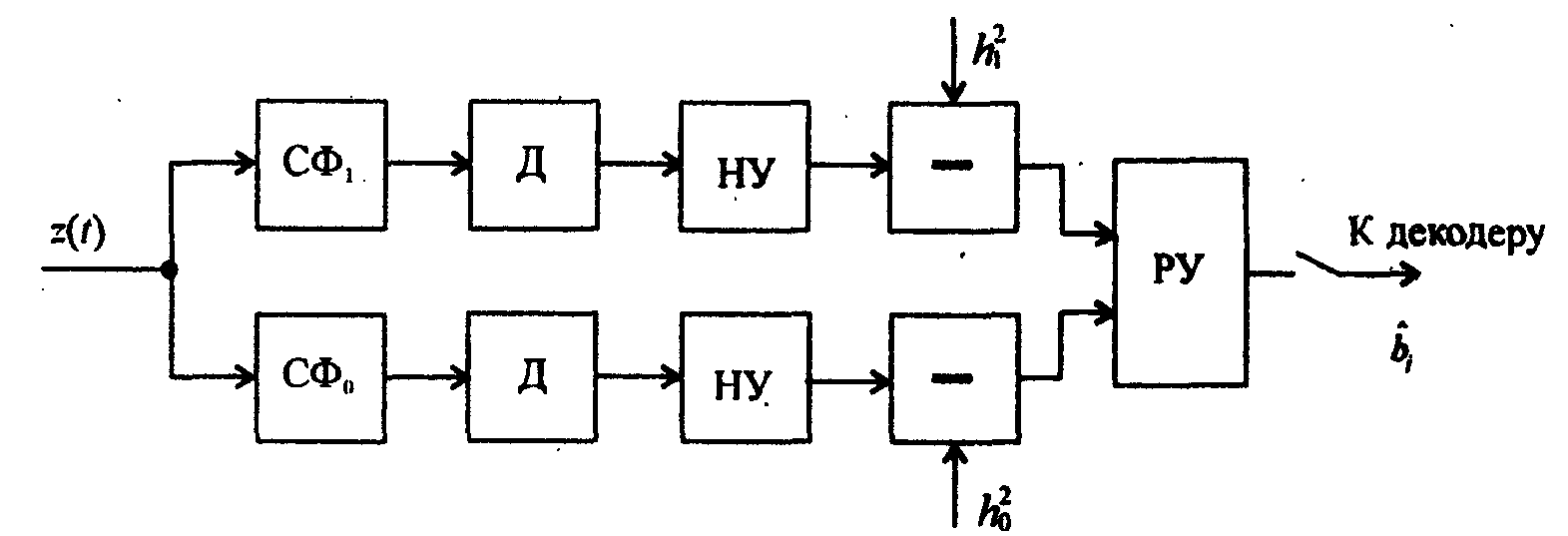
Идеальный детектор Д выделяет огибающую напряжения на выходе согласованного фильтра.

Алгоритм (13.9) и соответственно его реализация существенно упрощаются для систем с равными энергиями (). Для них с учётом монотонного характера функцииалгоритм оптимального некогерентного приёма можно записать так:

(13.11)

Для двоичной системы правило (13.11) упрощается и сводится к проверке одного неравенства

(13.12)

При его выполнении регистрируется символ 1, в противном случае – 0. При реализации алгоритма (13.12) не нужны блоки НУ и блоки вычитания. Схемы упрощаются.

36 Помехоустойчивость систем с различными видами дискретной модуляции при некогерентном приеме.

Исследования вероятности ошибок в канале с неопределённой фазой и аддитивным гауссовским шумом при поэлементном приёме показало, что минимальную вероятность ошибки обеспечивает система с равными энергиями, у которой сигналы удовлетворяют условиям ортогональности в усиленном смысле. Два сигнала x(t) и y(t) называются ортогональными в усиленном смысле, если соответствующие им аналитические сигналы итакже ортогональны. Определим вероятность ошибки при приёме по алгоритму (13.12) двоичных сигналов, удовлетворяющих условиям ортогональности в усиленном смысле. Если передаётся символ 1, то с учётом (11.11) и (13.12) имеем:

(13.13)

, где (13.14)

(13.15)

Если N(t) – нормальный стационарный белый шум с нулевым средним и односторонней спектральной плотностью мощности , то– нормально распределённая величина, так как она определяется линейной операцией над нормальным же случайным процессом. Коэффициенты корреляцииипри системе сигналов, ортогональной в усиленном смысле, равны нулю. Некоррелированность гауссовских величин означает их независимость. Следовательно, случайные величиныинезависимы, причёмимеет распределение Рэлея:

(13.16)

имеет распределение Райса:

(13.17)

Вероятность приёма символа 0 при передаче символа 1 определяется формулой:

_(13.18)

Используя методы теории вероятностей данное выражение можно преобразовать. В итоге получаем:

–для системы ортогональных сигналов в усиленном смысле (ЧМн) (13.19)

Такова же будет вероятность приёма символа 1 при передаче 0.

Для АМн: (13.20)

Для ОФМн (по методу сравнения фаз):

(13.21)