Криволинейные интегралы второго рода Задача о вычислении работы переменной силы. Определение криволинейного интеграла второго рода

Напомним, что если сила постоянна (по величине и по направлению), а путь прямолинеен, то работа этой силы на заданном пути равна скалярному произведению векторови:.

Пусть переменная сила действует вдоль кривой, меняясь при этом в каждой точке приложения как по модулю, так и по направлению, т.е., где,,― непрерывные вдоль данной кривой функции. При перемещении материальной точки вдоль данной кривойсиласовершает некоторую работу.

Чтобы найти эту работу разобьем произвольным образом кривую начастей,длиной.В каждой частивыберем произвольным образом точку, лежащую на кривой. Пусть― единичный вектор касательной к кривойв точке. Тогда вместо участкаможно приближенно рассматривать вектор, равный ему по длине и приблизительно по направлению, учитывая направление вдоль кривой.

Следовательно, ( если считать силу () постоянной на участке) элементарная работасилына участкеприближенно равна скалярному произведению:

.

Вся работа силы на криволинейном пути при­ближенно выражается формулой

.

Переходя к пределу при , где― длина наибольшей из элементарных дуг, получаем точное значение работы

.

Если данная интегральная сумма имеет предел при , то он называется криволинейным интегралом второго рода от вектор - функциипо кривойи обозначается

.

Таким образом, с механической точки зрения криволинейный интеграл второго рода есть работа переменной силы вдоль некоторой линии перемещения.

.

Отметим также, что определение криволинейного интеграла второго рода остается в силе и когда кривая замкнутая. В этом случае начальная и конечная точки совпадают. Криволинейный интеграл второго рода по замкнутому контуруобозначается следующим образом:

.

Отметим два свойства криволинейного интеграла.

Свойство 1.Криволинейный интеграл определяется подынтегральным выражением, формой кривой интегрирования и указанием направления интегрирования. При изменении направления интегрирования криволинейный интеграл меняет знак на противоположный.

Свойство 2.Разобьем кривую интегрирования точкой на части и, тогда

.

Криволинейный интеграл второго рода в координатной форме

При определении криволинейного интеграла второго рода элементарная работа силына участкенаходилась как скалярное произведение вектораи вектора, приближенно равного по длине и направлению участку. Вместо вектора, в качестве вектора, близкого кможно взять вектор, начало и конец которого совпадают с началом и концом участка.

Найдем скалярное произведение векторов ив координатной форме как сумму произведений соответствующих координат:

Переходя к пределу при , где― длина наибольшей из элементарных дуг, получаем точное значение работы

.

Следовательно, криволинейный интеграл второго рода в скалярной координатной форме имеет вид:

или, в более краткой форме

.

Вычисление криволинейных интегралов второго рода

Пусть линия задана параметрически

:.

Тогда по определению дифференциала

Отметим начало дуги точкой, конец — точкой. В этом случае говорят, что задано направление перемещения по кривой от точкик точкеи тем самым указано направление ориентирующего вектора.

Покажем, что вычисление криволинейного интеграла второго рода по линии заданной параметрически, сводится к вычислению однократного определенного интеграла по параметру:

А в случае плоской кривой, когда , последняя формула примет вид:

Замечание.Для плоской кривой, заданной уравнением,криволинейный интеграл второго рода в координатной скалярной форме сводится к определенному интегралу по переменной

(Выбрана ориентация , при которой,соответствуют началу и окончанию пути интегрирования.)

Если кривая задана уравнением,, то при соответствующей ориентации интегрирование по переменнойбудет осуществляться отдо:

.

Пример. Вычислить, где— отрезок прямой с началом в точкеи концом в точке.

Решение. Изобразим на рисунке линию интегрирования.

Воспользуемся формулами параметрических уравнений прямой с направляющим вектором , проходящей через начальную точку с координатами:

Запишем параметрические уравнения прямой, которой принадлежит отрезок , приняв за направляющий вектор прямойвектор.

.

Начальной точкой отрезка является точка. Следовательно, параметрические уравнения этой прямой:

Из полученных уравнений находим, что точке соответствует значение параметра, а точкезначение.

По определению дифференциала

Подставляя в интеграл значения и, а также учитывая значения параметраи, соответствующие началу и концу дуги, получим:

.

Пример. Вычислить, где— отрезок прямой с началом в точкеи концом в точке.

Решение. Изобразим на рисунке линию интегрирования.

Воспользуемся формулами параметрических уравнений прямой с направляющим вектором , проходящей через начальную точку с координатами:

Запишем параметрические уравнения прямой, которой принадлежит отрезок , приняв за направляющий вектор прямойвектор, т. е..

Начальной точкой отрезка является точка. Следовательно, параметрические уравнения этой прямой:

Из полученных уравнений находим, что точке соответствует значение параметра, а точкезначение.

По определению дифференциала

Учитывая, что и, подставляем в интеграл только значенияи, а также значения параметраи, соответствующие началу и концу дуги

.

Пример. Вычислить, где—плоская кривая, являющаяся частью параболыот точкидо точки.

Решение. Изобразим на рисунке линию интегрирования.

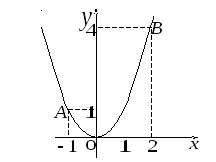
Воспользуемся формулой:

В данном случае соответствуют началу и окончанию пути интегрирования,, следовательно:

.