Вычисление двойного интеграла в полярной системе координат

Осуществим в двойном интеграле , заданном в декартовой системе координат, замену переменных по формулам перехода к полярной системе координат:,. В этом случае подынтегральная функция будет зависеть от полярных координати:. Пусть область такова, что любой луч, выходящий из начала координат и проходящий через внутреннюю точку области, пересекает границу не более, чем в двух точках . Линии, ограничивающие область, имеют уравнения,, где,. Такую область, применительно к полярной системе координат, будем называть правильной (см. рис.).

Поскольку предел интегральной суммы не зависит от способа разбиения фигуры на элементарные, подобное разбиение можно осуществить с помощью лучей , проходящих через начало координат, и концентрических окружностейс центрами в начале координат. При пересечении двух окружностей радиусов,и лучей, проведенных под угламии, образуется элементарная криволинейная фигура. Ее, с точностью до бесконечно малых высшего порядка, можно рассматривать как прямоугольник со сторонами, и, площадь которого.

Следовательно, двойной интеграл в полярных координатах имеет вид

.

Итак, если область является правильной применительно к полярным координатам, то вычисление двойного интеграла сводится к вычислению двукратного интеграла по переменными. Для расстановки пределов интегрирования из полюса проводят ограничивающие лучии, записывают уравнения линий входа в область(AMВ) —и выхода из нее(АКВ) —. Тогда,.

Как правило, внешний интеграл вычисляется по переменной , а внутренний — по. На основании изложенного имеет место следующая формула вычисления двойного интеграла в полярных координатах:

,

при этом лучи и, и кривые, ограничивают фигуру, по которой осуществляется вычисление двойного интеграла.

Пример. Вычислить двойной интеграл по области, ограниченной линиями:,,,.

Решение.Изобразим на рисунке заданную область интегрирования.

Если рассматривать данную область как стандартную относительно оси , то область интегрирования необходимо разбить на две области, а повторный интеграл представить как сумму двух интегралов, так как снизу функциявыражена двумя аналитическими выражениями (и), то область интегрирования необходимо разбить на две области, а повторный интеграл представить как сумму двух интегралов. Аналогичная ситуация возникнет и для оси. При этом, как и в первом случае, так и во втором мы придем к необходимости нахождения достаточно сложных интегралов. Так как линиями, частично ограничивающими область, являются окружности, имеет смысл перейти к полярной системе координат.

Перейдем к полярным координатам по формулам:

,.

Тогда уравнение в полярных координатах запишется в виде:

.

Уравнение получит вид:

.

Ограничение в полярных координатах будет иметь вид:

.

Аналогично .

Подынтегральная функция примет вид:.

Область является правильной применительно к полярным координатам, следовательно, можем использовать формулу:

.

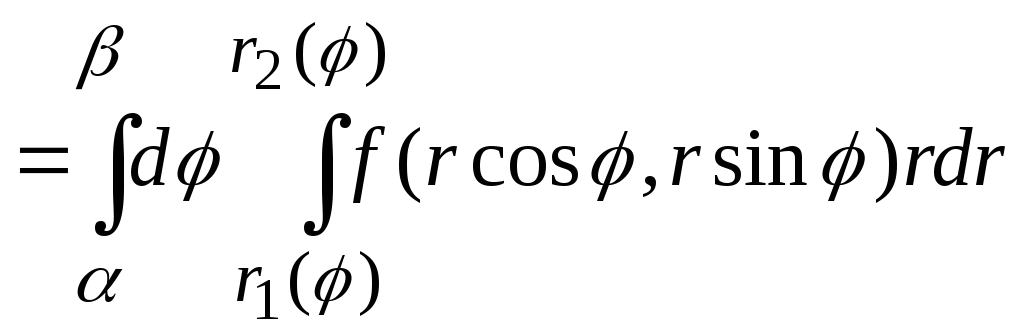Получаем:

.