
контр робота ЗЕЕ-10-ск
.docЧастина І.
Задача 1.
Розв’язати
систему лінійних рівнянь: а) методом
Гаусса; б) за формулами Крамера; в) методом
оберненої матриці (з цією метою ввести
необхідні позначення і записати систему
у вигляді матричного рівняння, розв’язком
якого буде стовпець невідомих; для
перевірки обчислень оберненої матриці
скористатися однією з рівностей
![]() ).
).
|
Вар |
|
Вар |
|
|
1. |
2x – y – z = 3; 3x + 4y – 5z = 1; – 5x – 4y + 3z = – 15. |
2. |
4x + 9y + z = – 27; – 5x – 4 y + 4z = – 1; 2x – y – 3 z = – 5. |
|
3. |
– 4x – 3y + 4z = – 12; – 5x – 4y + 5z = – 22; – 2x + 3y – z = – 9. |
4. |
2x – y + 5z = – 2; 4x + 4y + 5z = 12; 4x – 4y – 5z = 22. |
|
5. |
4x + 4y – 3z = – 34; – 5x – 2y + 2z = 41; 2x – 4y – 3z = 1. |
6. |
3x – 8y + 5z = – 3; – 6x – 3y + 4z = – 1; 8x – 2y – 2z = – 21. |
|
7. |
7x – 2y + 4z = 29; – 5x + 3y – 2z = 10; – 3x – 5y + z = 9. |
8. |
– 5x – y – 4z = 22; 2x + 3y – 4z = 13; 8x + 5y + 2z = 5.. |
|
9. |
5x – 3y – 2z = – 2; 2x – 4y – 2z = 29; 5x + 5y + z = 41. |
10. |
– 5x – 2y – 4z = – 2; – 2x – 4y – 3z = 1; 4x + 3y + 4z = – 2. |
|
11. |
3x – y – 2z = – 2; 5x + 9y – z = 3; – 2x + 2y + z = 3. |
12. |
9x – y – z = 6; – 5x + 9y – 5z = 2; 2x – 2y + 2z = 7. |
|
13. |
x – 3y + 3z = 8; 2x – y – z = – 3; 3x + 6y + 4z = 9. |
14. |
– x + 2y + 2z = 1; 2x – 8y + 4z = 9; 6x – 7y – z = 4. |
|
15. |
7x + 2y – 3z = 8; 2x – y – z = 5; x + 2y – z = 3. |
16. |
x + 2y – z = 2; 2x – y + z = – 1; – 3x + y + 2z = – 3. |
|
17. |
2x + z = 1; 4x + 3y + 5z = 8; 3x + 2y + 6z = 7. |
18. |
3x – 2y + 2z = – 1; 5x + 9y – 6z = 3; 7x + 6y + 2z = 0. |
|
19. |
x + y – 2z = 3; 3x + 2y + z = 8; 4x + 6y + 3z = 9. |
20. |
4x – 8y – 5z = – 5; 2x + 2y + 4z = 9; x + 3y + 5z = 10. |
|
|
|
|
|
|
21. |
– 5x – 3y – 2z = 7; 7x – 9y – 3z = 18; – 5x – 5y – 3z = 14. |
22. |
2x – 3y – 2z = 7; 3x + 8y – 3z = 1; 5x – 5y - 3z = 8. |
|
23. |
2x – y + 7z = – 1; 3x + 5y – z = 4; – 3x – 5y – 3z = 3. |
24. |
9x – 3y – 2z = 7; 7x – 9y – 3z = 18; – 5x – 5y – 3z = 14. |
|
25. |
– 4x – 3y + 3z = 7; 7x + 2y + 2z = – 2; – 5x + y – 3z = 3. |
26. |
3x – 3y – 2z = 7; 7x + 8y + 7z = 18; 9x – 5y – 3z = 14. |
|
27. |
4x – 3y – 2z = 7; 7x – 9y – 3z = 18; – 5x – 5y – 3z = 14. |
28. |
– 4x – 3y – 2z = 7; 3x – 9y – 3z = 18; – 5x – 5y – 3z = 14. |
|
29. |
7x – 3y – 2z = 7; 5x + 4y – 3z = 9; 4x – 5y – 3z = 14 |
30. |
6x – 3y – 2z = 7; x – 3y – z = 6; – 5x – 5y – 3z = 14. |
Задача 2.
Відомі
координати векторів
![]() в ортонормованому базисі. Необхідно:
в ортонормованому базисі. Необхідно:
1. обчислити
![]()
2.
знайти координати одиничних векторів
![]() і
і
![]() ,
колінеарних вектору
,
колінеарних вектору
![]()
3.
обчислити
![]() ,
,
![]() ,
,![]() ;
;
4. обчислити роботу
А сили
![]() при
переміщені матеріальної точки з точки
D(5,9,-8)
у
точку E(4,7,-6);
при
переміщені матеріальної точки з точки
D(5,9,-8)
у
точку E(4,7,-6);
5. знайти
момент
![]() сили
сили
![]() відносно точки P(-2,3,5),
якщо
сила прикладена до важеля
PQ
у
точці Q(-1,2,8);
відносно точки P(-2,3,5),
якщо
сила прикладена до важеля
PQ
у
точці Q(-1,2,8);
6.
перевірити, чи утворюють базис вектори
![]() .
Якщо утворюють, то знайти координати
вектора
.
Якщо утворюють, то знайти координати
вектора
![]() в
цьому базисі.
в
цьому базисі.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Задача 3. Відомі координати вершин трикутника ABC. Необхідно:
1. знайти
координати нормального вектора
![]() і кутовий коєфіцієнт
і кутовий коєфіцієнт
![]() прямої ВС;
прямої ВС;
2. з’ясувати, чи є трикутник АВС прямокутним;
3. скласти рівняння прямої АА1, паралельної до прямої ВС;
4. скласти рівняння висоти АН;
5. скласти рівняння медіани ВМ;
6. обчислити координати точки перетину Е прямих АН і ВМ;
7. накреслити трикутник АВС за координатами його вершин, побудувати прямі АА1, АН, ВМ за їх рівняннями та перевірити відповідність координат точки Е малюнку.

![]()



Задача 4. Відомі координати точок А, В, С, D. Необхідно:
1. побудувати піраміду АВСD за координатами її вершин;
2. скласти рівняння площини АВС;
3. знайти висоту hD як відстань від точки D до площини АВС;
4. знайти рівняння висоти hD;
5. знайти точку H перетину висоти hD з площиною АВС;
6. знайти кут між висотою DH та ребром DC;
7. знайти площу трикутника АВС;
8. знайти об’єм піраміди;
9.
перевірити,
що
![]() .
.
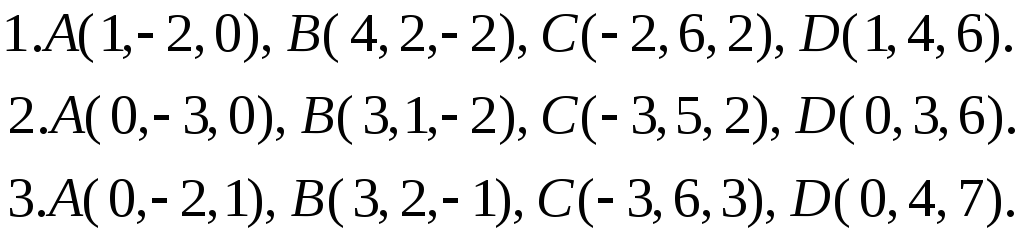
![]()
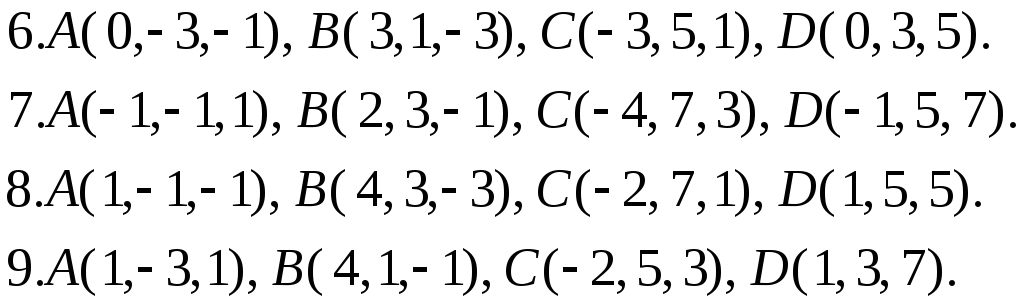
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
Задача 5. Дано рівняння деяких ліній. Необхідно:
-
визначити типи лінії;
-
побудувати лінії за їх рівнянням.
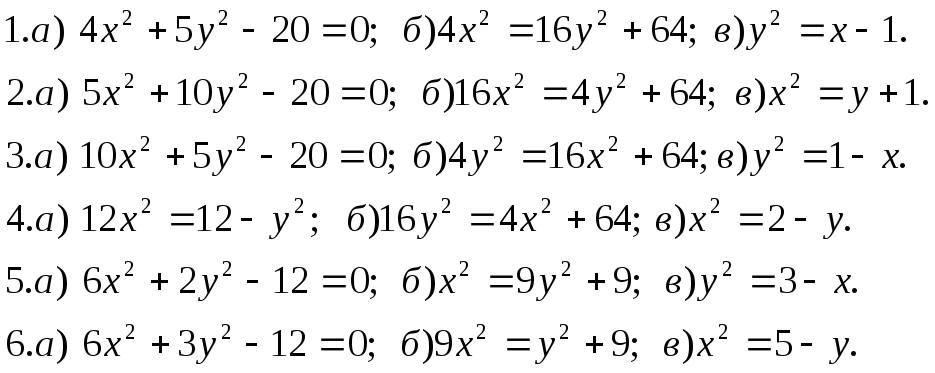
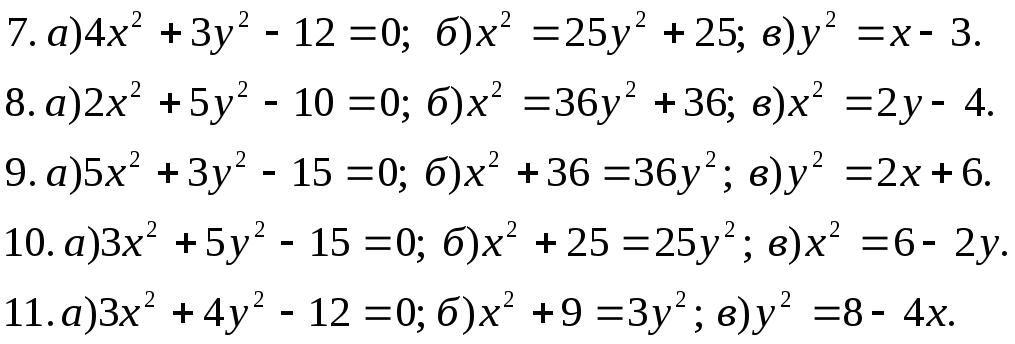
![]()
![]()
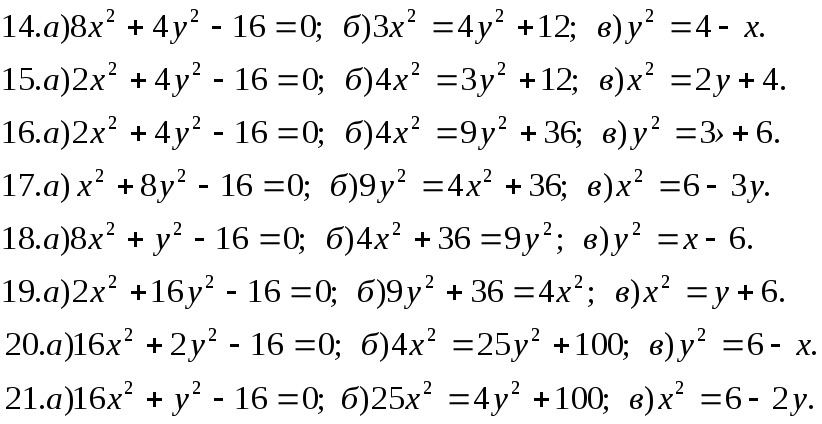
![]()
![]()

![]()
Задача 6.
За
варіантами 1 - 30 дано полярне рівняння
лінії
![]() (
(![]() -полярний кут,
-полярний кут,
![]() - полярний радіус). Необхідно:
- полярний радіус). Необхідно:
а) побудувати за точками задану лінію;
б)
використовуючи зв’язок
між полярними та прямокутними координатами,
рівняння
![]() перетворити в рівняння
перетворити в рівняння
![]() у прямокутних координатах.
у прямокутних координатах.
Вказівка.
Скласти таблицю значень
![]() і
і
![]() :
:
|
|
|
|
|
… |
|
|
|
|
|
… |
Куту
![]() надавати значень
надавати значень
![]()
![]() .
Побудувати точки
.
Побудувати точки
![]() і сполучити ці точки плавною лінією.
Для перевірки обчислень, рівняння
і сполучити ці точки плавною лінією.
Для перевірки обчислень, рівняння
![]() шляхом виділення повних квадратів
звести до вигляду
шляхом виділення повних квадратів
звести до вигляду
![]()
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
16. |
|
|
17. |
|
18. |
|
|
19. |
|
20. |
|
|
21. |
|
22. |
|
|
23. |
|
24. |
|
|
25. |
|
26. |
|
|
27. |
|
28. |
|
|
29. |
|
30. |
|
Задача 7. Дано комплексні числа z1 і z2.
а)
Обчислити вираз
![]() Для контролю перевірити рівність
Для контролю перевірити рівність
![]() .
.
б)
обчислити
![]() іншим способом, виконуючи дії з числами
іншим способом, виконуючи дії з числами
![]() ,
,
![]() ,
,![]() в показниковій формі (для контролю
відповідь за допомогою формули Ейлера
записати в алгебраичному вигляді і
порівнняти з результатом пункту а).
в показниковій формі (для контролю
відповідь за допомогою формули Ейлера
записати в алгебраичному вигляді і
порівнняти з результатом пункту а).
|
|
|
|
|
|
|
|
1. |
|
|
2. |
|
|
|
3. |
|
|
4. |
|
|
|
5. |
|
|
6. |
|
|
|
7. |
|
|
8. |
|
|
|
9. |
|
|
10. |
|
|
|
11. |
|
|
12. |
|
|
|
13. |
|
|
14. |
|
|
|
15. |
|
|
16. |
|
|
|
17. |
|
|
18. |
|
|
|
19. |
|
|
20. |
|
|
|
21. |
|
|
22. |
|
|
|
23. |
|
|
24. |
|
|
|
25. |
|
|
26. |
|
|
|
27. |
|
|
28. |
|
|
|
29. |
|
|
30. |
|
|
