Пример решения задачи

(рабочее тело – водяной пар)

Дано:

V₁ = 10 л = 10^-2 м³

Р₁ = 8·10⁵ Па

Т₁= 800 K

d = 0,3·10^-9 м

M = 0,018 кг/моль

i = 6; n₁= 2;

n₂= 2;

m-? V₂ - ? V₃ - ? V₄ - ? T₂ - ?

Р₂ - ? Р₃ - ? P₄ - ? - ? <l₁> - ? D₂ - ? E_П - ? E_В - ? с_р - ? с_v - ? A₁₂ - ? A₂₃ - ? A₃₄ - ? A₄₁ - ?

Q₁ - ? Q₂ - ? A - ? η - ?

ΔU₁₂ - ? ΔU₂₃ - ? ΔU₃₄ - ? ΔU₄₁ - ?

Масса m рабочего тела определяется из уравнения Менделеева-Клапейрона для состояния (1)

(1)

P₁,V₁,T₁ - давление, объем, температура (по шкале Кельвина) для состояния (1), М – молярная масса, R=8,31 - универсальная газовая постоянная.

Участок (1) - (2) – изотермическое расширение (постоянная температура T₁). Запишем уравнение Менделеева - Клапейрона для состояния (2)

(2)

Сопоставив формулы (1) и (2), получим

Определяем давление:

(3)

По условию задачи, при изотермическом расширении (1)-(2), объем V₂ возрастает в n₁ раз, т.е. .

Из формулы (3) получаем:

м³

Участок (2) - (3) - адиабатное расширение в n₂ раз. Согласно уравнению для адиабатного процесса

= const ,

где - показатель адиабаты.

- число степеней свободы молекулы. Для одноатомных молекул (Ar, He) =3, для двухатомных молекул (N,O) =5, для многоатомных молекул (CO, HO) =6.

Внимание! В случае, когда рабочим телом является воздух, число степеней свободы і = 5.

Для процесса (2) - (3) уравнение Пуассона принимает вид

Находим (4)

По условию задачи м,

Тогда уравнение (4) примет вид

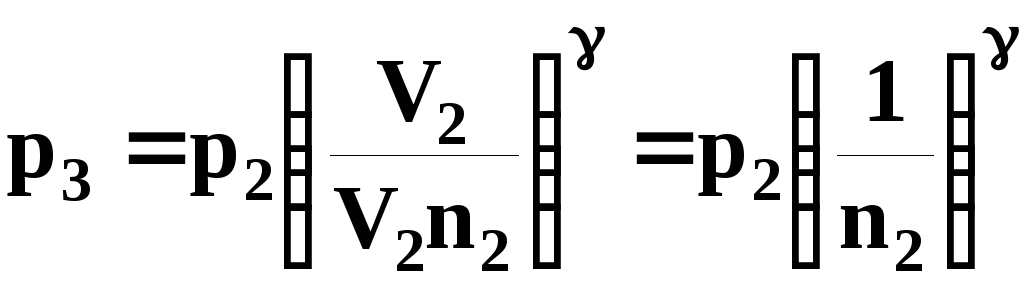
В данной задаче рабочее тело – водяной пар. Для него число степеней свободы молекулы =6. Вычисляем показатель адиабаты

Находим давление в состоянии (3)

Точка 4 цикла находится на пересечении изотермы (3) - (4) и адиабаты (4) - (1). Для изотермы (3)-(4) справедливо соотношение

(5)

Для адиабаты (4) - (1)

(6)

Представляем (5) в (6)

После упрощения получаем:

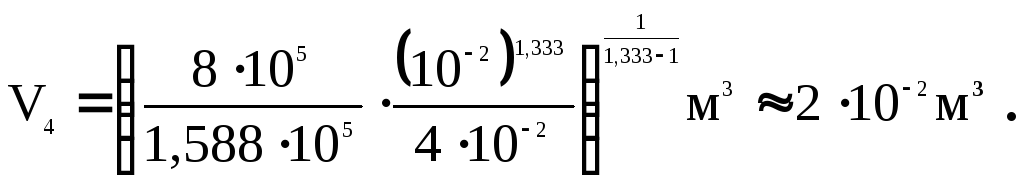
По формуле (5) вычисляем P₄

Для контроля проверим выполнение соотношения (5)

Соотношение (6) выполняется с достаточной точностью

Для адиабатического процесса

= const (7)

Тогда для адиабаты (2) - (3) можно записать

(8)

Из формулы (8) определяем температуру T состояния (3)

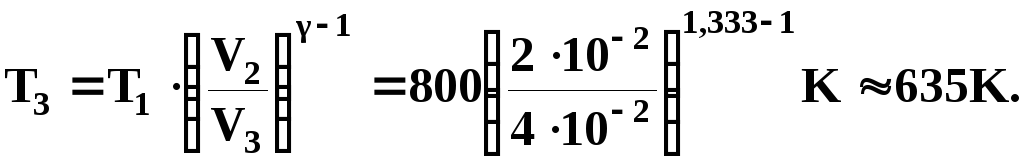
Параметры состояний 1,2,3,4 приведены ниже в таблице.

Состояние	P, Па	V, м3	T, К
1
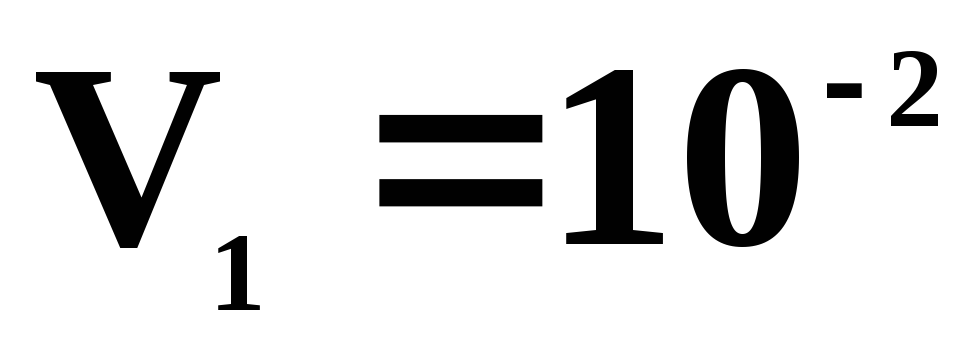
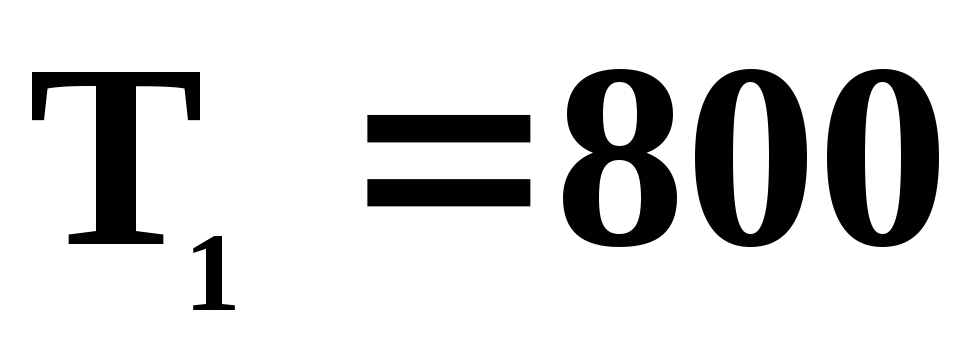
2
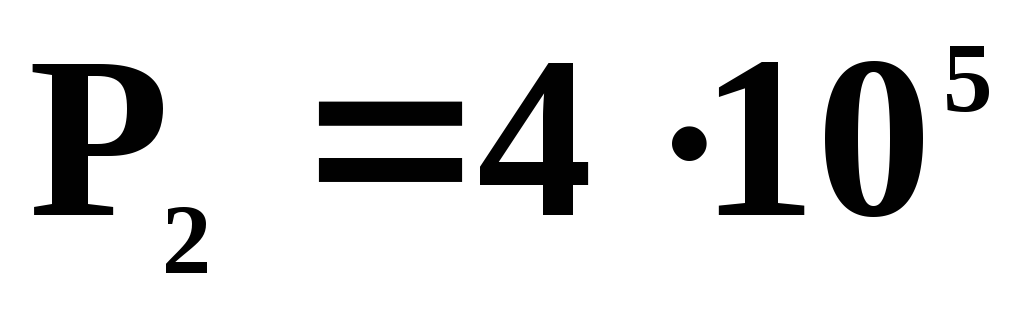
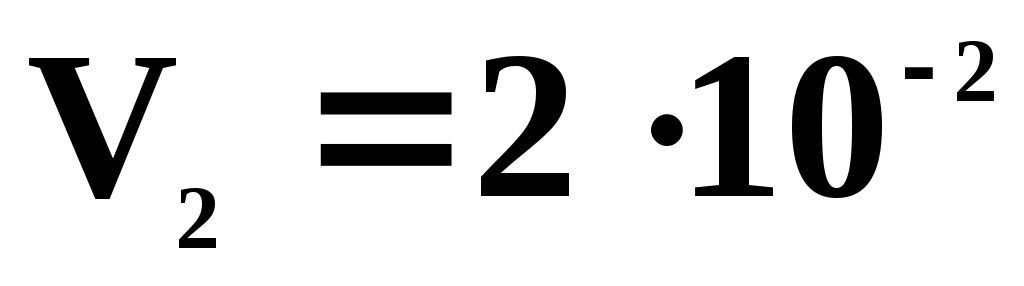
3
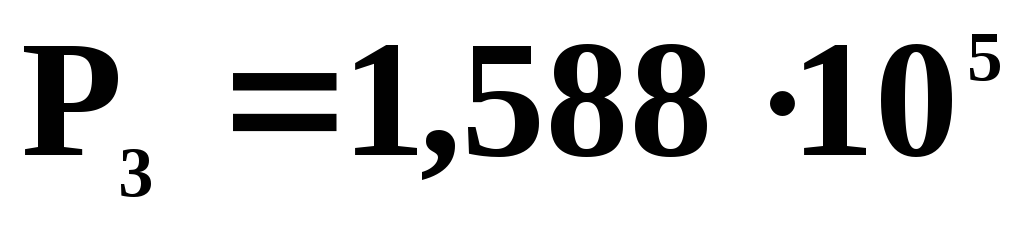
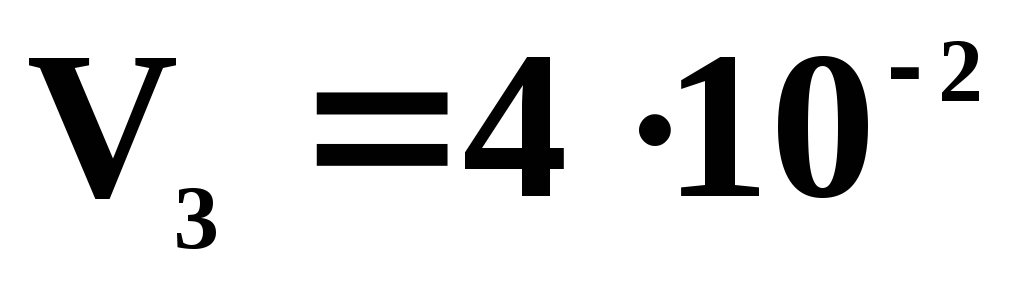
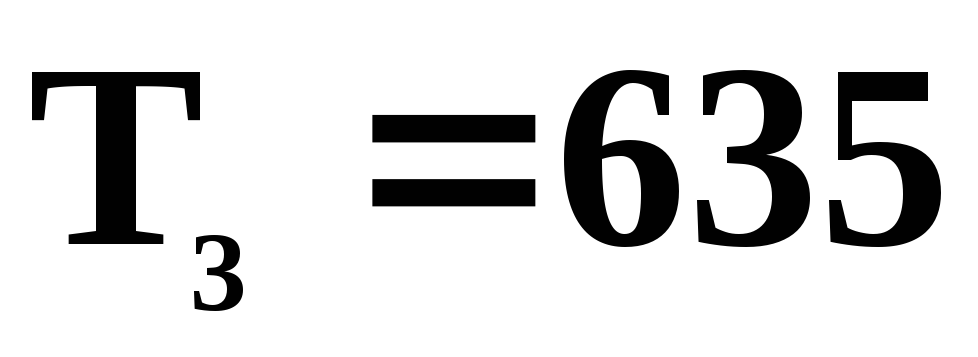
4

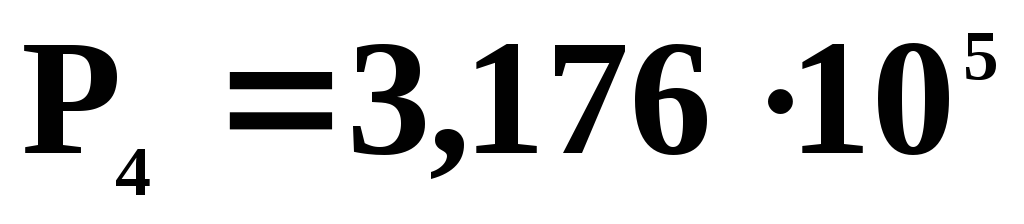
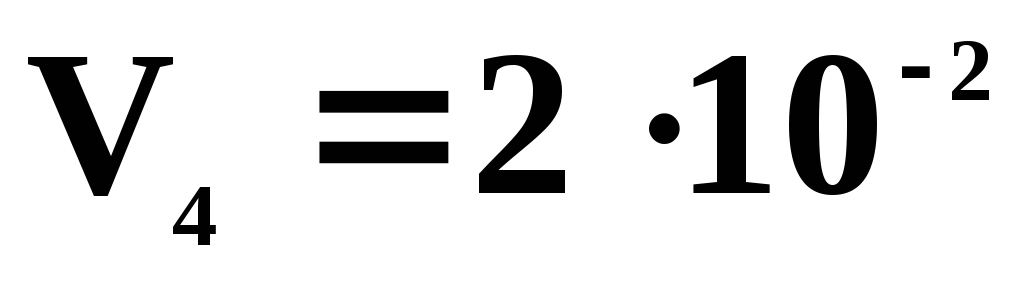
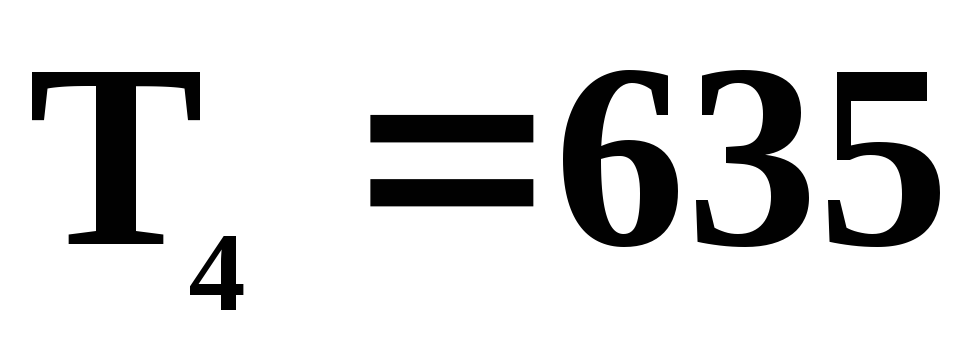
Плотность водяного пара в состоянии (3):

Средняя длина свободного пробега молекул водяного пара в состоянии (1):

(9)

- эффективный диаметр молекул (табличная величина), - концентрация молекул в состоянии (1)

(10)

- число молекул, - число молей,-число Авогадро. Подставляем (10) в (9) и вычисляем среднюю длину свободного побега молекул

(11)

Коэффициент диффузии D₂ молекул водяного пара в состоянии

(12)

где - средняя скорость молекул водяного пара в состоянии 2,- средняя длина пробега молекул в состоянии 2.

Для аналогично формуле (11) можно записать

После подстановки выражений и<l> в (12) получаем коэффициент диффузии в состоянии (2)

Среднее значение кинетической энергии поступательного движения всех молекул водяного пара

(13)

-среднее значение кинетической энергии поступательного движения одной молекулы, - постоянная Больцмана.

Среднее значение кинетической энергии вращательного движения молекул:

- число вращательных степеней свободы молекул. Для трехатомных молекул , для двухатомных, для одноатомных.

Теплоемкость при постоянном давлении для данной массы газа

- молярная теплоемкость идеального газа при постоянном давлении

Теплоемкость при постоянном объеме для данной массы газа

- молярная теплоемкость идеального газа при постоянном объеме

Работа изотермического процесса

(14)

V_н- начальный объем, V_к- конечный объем

При изотермическом расширении 1 - 2 работа газа равна

При изотерическом сжатии 3 – 4 работа газа равна

Работа адиабатического процесса равна

(15)

Т_н - начальная температура

Т_к - конечная температура

Работа адиабатического расширения 2-3

Работа адиабатического сжатия 4-1

Работа A, совершаемая тепловой машиной за один цикл равна

Определим количество теплоты , полученное от нагревателя и количество теплоты, отданное рабочим теплом охладителю.

Согласно первому началу термодинамики

(16)

- количество теплоты, переданное системе, - изменение внутренней энергии системы,-работа, совершенная системой.

Внутренняя энергия идеального газа

Изменение внутренней энергии

(17)

Рабочее тело получает теплоту от нагревателя при изотермическом расширении (1) - (2). При этомU = 0. Тогда согласно равенству (16)

При изотермическом сжатии (3) - (4) охладителю отдается количество теплоты

Адиабатические процессы 2 - 3 и 4-1 проходят без теплообмена с окружающей средой. Тогда работа , совершенная за один цикл, будет равна

Это значение совпадает со значением, полученным выше путем суммирования работ для отдельных участков цикла.

Коэффициент полезного действия тепловой машины равен отношению работы , совершенной за один цикл, к количеству теплоты, полученному от нагревателя

Для цикла Карно КПД можно определить через температуры нагревателя и охладителя

Для изотермических процессов (1) - (2) и (3) - (4) изменение внутренней энергии равно

Так как при адиабатических процессах нет теплообмена с окружающей средой , из формулы (16) следует

Тогда изменение внутренней энергии при адиабатическом расширении (2) - (3) будет равно

Изменение внутренней энергии при адиабатическом сжатии (4) - (1) равно

Внутренняя энергия является функцией состояния. Поэтому при совершении цикла, кода система возвращается в исходное состояние, суммарное изменение внутренней энергии . Согласно полученным данным это соотношение действительно выполняется: