
- •Министерство образования и науки украины
- •Издается в авторской редакции
- •Введение
- •1. Содержание курсовой работы
- •2. Задание на курсовой проект
- •3. Расчет параметров г-образной схемы замещения
- •4. Расчет мощности, потребляемой из сети
- •5. Расчет характерных точек механической характеристики
- •6. Построение механической и энергомеханической характеристик при номинальных напряжении и частоте
- •7. Выбор закона регулирования в зависимости от заданной характеристики момента нагрузки
- •8. Построение механических характеристик при выбранном законе регулирования
- •8.1. Закон управления при постоянной нагрузке
- •8.2. Закон управления при нелинейно спадающем моменте нагрузки
- •8.3. Закон управления при вентиляторном характере момента нагрузки
- •9. Скалярное управление скоростью асинхронного двигателя
- •9.1. Система управления пч-ад со скалярной -компенсацией
- •9.2. Система управления пч-ад при скалярном управлении с отрицательной обратной связью по скорости
- •9.2.1. П-регулятор скорости
- •9.2.2. Пи-регулятор скорости
- •Содержание
- •49600, Днепропетровск-5, пр. Гагарина, 4
6. Построение механической и энергомеханической характеристик при номинальных напряжении и частоте
Уравнение
механической характеристики представляет
собой зависимость скольжения
![]() (частоты вращения
(частоты вращения![]() )
от момента
)
от момента![]() :
:
|
|
(25) |
Энергомеханические
характеристики представляю собой
зависимость токов
![]() статора и ротора
статора и ротора![]() от скольжения
от скольжения![]() .
.
Ток
![]() вычисляется по формуле:
вычисляется по формуле:
|
|
(26) |
Ток
![]() является векторной суммой токов ротора
является векторной суммой токов ротора![]() и тока намагничивания
и тока намагничивания![]() .
Модуль тока статора в этом случае будет
равен:
.
Модуль тока статора в этом случае будет
равен:
|
|
(27) |
где
 - сдвиг по фазе тока ротора.
- сдвиг по фазе тока ротора.
Механическую и энергомеханические характеристики в соответствии с уравнениями (25) – (27) для двигательного режима работы построить на одном графике в среде MathCad.
7. Выбор закона регулирования в зависимости от заданной характеристики момента нагрузки
В задании на курсовую работу (приложение 1) указана характеристика момента нагрузки:
постоянный момент нагрузки,
нелинейно спадающий момент нагрузки,
вентиляторный характер момента нагрузки.
В соответствии с вариантом задания момент нагрузки рассчитывается по одной из следующих формул.
Постоянный момент нагрузки. В этом случае принимается, что момент нагрузки равен номинальному моменту двигателя:
|
|
(28) |
Нелинейно спадающий момент нагрузки:
|
|
(29) |
где
![]() - частота вращения ротора,
- частота вращения ротора,![]() ;
;![]() - коэффициент, определяющий крутизну
изменения момента нагрузки,
- коэффициент, определяющий крутизну
изменения момента нагрузки,![]() .
.
Момент вентиляторной нагрузки:
|
|
(30) |
где
![]() - момент холостого хода, Нм;
- момент холостого хода, Нм; - коэффициент, определяющий крутизну
изменения момента нагрузки,
- коэффициент, определяющий крутизну
изменения момента нагрузки,![]() .
.
8. Построение механических характеристик при выбранном законе регулирования
При изменении
частоты напряжения на статоре будут
изменяться синхронная частота вращения
![]() ,
скольжение
,
скольжение![]() и индуктивные сопротивления рассеивания
статора и ротора
и индуктивные сопротивления рассеивания
статора и ротора![]() :
:
|
|
(31) |
|
|
(32) |
|
|
(33) |
С учетом выражений (31), (33) уравнение (25) механической характеристики запишется в виде:

|
|
(34) |
8.1. Закон управления при постоянной нагрузке
При постоянном
нагрузочном моменте
![]() соотношение между напряжением и частотой
определяется законом
соотношение между напряжением и частотой
определяется законом
|
|
(35) |
С учетом уравнения (35) формула (34) запишется в виде:

|
|
(36) |
Механические характеристики асинхронного двигателя для двигательного режима работы строятся по уравнениям (36), (32) в среде MathCad. Характеристики строятся на одном графике для следующих значений частоты напряжения статора:
 ,
, ,
, ,
, ,
, .
.
На том же графике строится уравнение момента нагрузки для следующего случая:
момент нагрузки равен номинальному моменту двигателя
 .
.
8.2. Закон управления при нелинейно спадающем моменте нагрузки
При нелинейно спадающем моменте нагрузки уравнение момента нагрузки имеет вид (29):
|
|
(37) |
В этом случае соотношение между напряжением и частотой определяется законом
|
|
(38) |
С учетом уравнения (38) формула (34) запишется в виде:

|
|
(39) |
Механические характеристики асинхронного двигателя строятся по уравнениям (39), (32) для двигательного режима работы в среде MathCad. Характеристики строятся на одном графике для следующих значений частоты напряжения статора:
 ,
,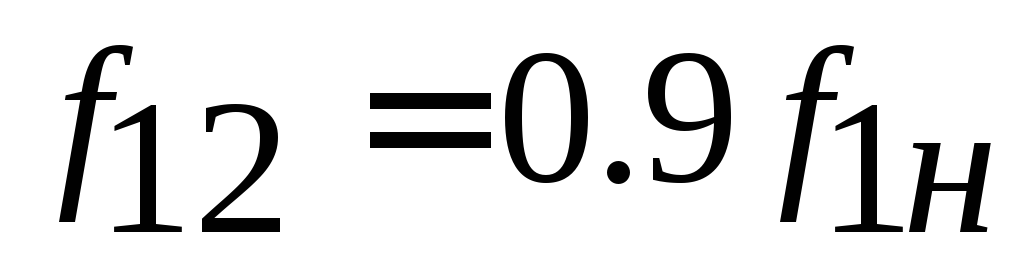 ,
, ,
, ,
, ,
,
На том же графике строится уравнение момента нагрузки для следующего случая:
нелинейно спадающий момент нагрузки
 .
.

 ,
Нм.
,
Нм. ,
А.
,
А. ,
, ,
, ,
, .
.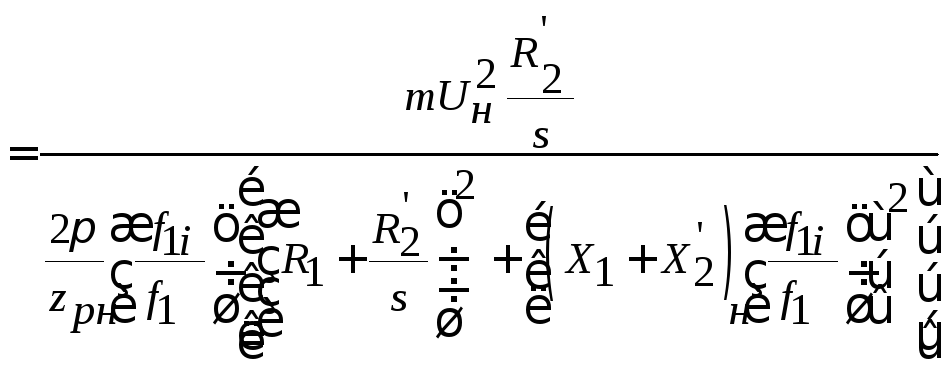 .
. .
. .
. .
. .
. .
.