
- •Глава 1 Основні поняття термодинаміки
- •1.1 Термодинамічна система
- •1.2 Фаза
- •1.3 Компонент
- •1.4 Термодинамічні параметри стану системи
- •1.5 Термодинамічний потенціал системи
- •1.6 Хімічний потенціал атомів компонентів
- •1.7 Рівновага в гетерогенній системі
- •1.8 Правило фаз Гіббса
- •1.9 Фазовий простір Гіббса
- •Глава 2 аналіз діаграм фазових рівноваг у подвійних системах
- •2.1 Діаграми стану з необмеженою розчинністю компонентів у твердій і рідкій фазах
- •2.1.1 Двокомпонентна система
- •2.2 Діаграми фазових рівноваг в системах з обмеженою розчинністю компонентів у твердих фазах
- •2.2.1 Діаграма стану з евтектичною рівновагою фаз
- •2.2.2 Діаграма стану з перитектичною рівновагою фаз
- •2.3 Діаграми стану з поліморфізмом компонентів
- •2.3.1 Однокомпонентна система
- •2.3.2 Двокомпонентна діаграма стану з поліморфізмом одного компоненту
- •2.3.3 Діаграма стану з евтектоїдною рівновагою фаз
- •2.4 Діаграми стану з проміжними фазами
- •2.5 Використання принципів термодинаміки незворотних процесів до аналізу фазових переходів в реальних системах
2.3.2 Двокомпонентна діаграма стану з поліморфізмом одного компоненту
На рис. 12, а приведена діаграма стану з поліморфізмом компоненту А.
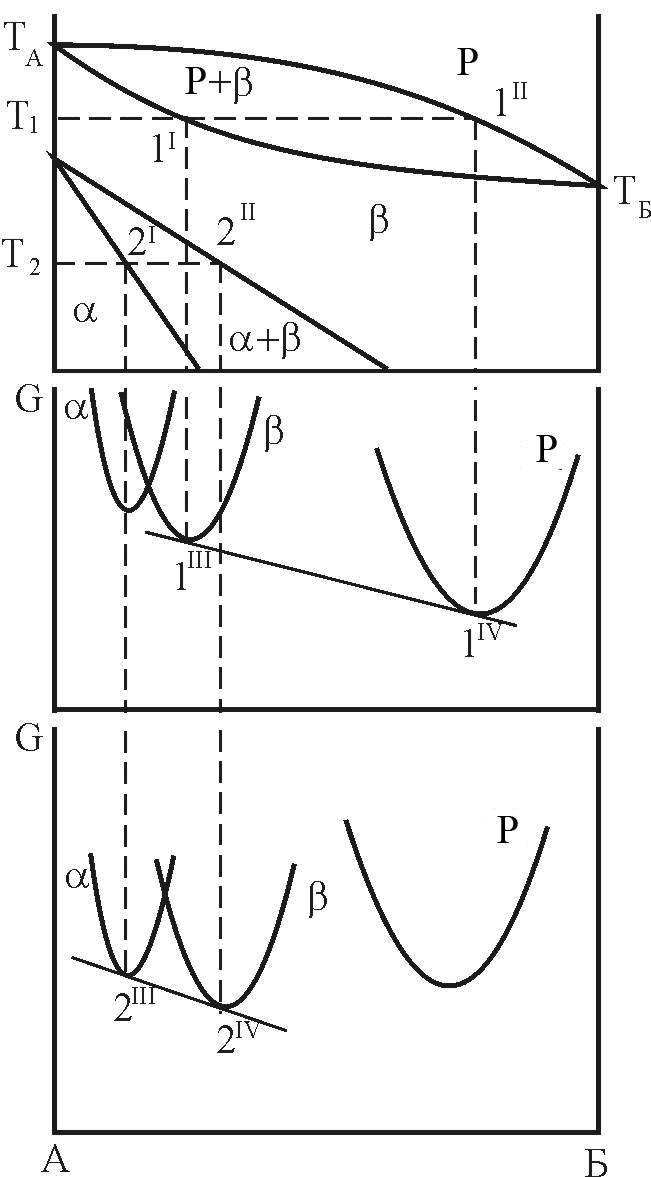
Рисунок 12 – Взаємне розташування кривих ізобарно-ізотермічного потенціалу і фазових областей діаграми стану з поліморфізмом компоненту А
Твердий
a-розчин
на базі низькотемпературної модифікації
![]() має обмежену область стійкості.
Високотемпературна модифікація
має обмежену область стійкості.
Високотемпературна модифікація![]() є ізоморфною по структурі кристалічної
гратки компоненту Б. Це обумовило
утворенняb
твердого
розчину в усьому інтервалі концентрацій
- від 0 % Б до 100 % Б.
є ізоморфною по структурі кристалічної
гратки компоненту Б. Це обумовило
утворенняb
твердого
розчину в усьому інтервалі концентрацій
- від 0 % Б до 100 % Б.
Умова рівноваги фаз визначається, як і у раніше розглянутих діаграмах, з умови рівності хімічних потенціалів атомів компонентів у кожній з фаз.
Зокрема,
рівновага
![]() при Т=Т1
(рис. 12, а) визначається з умови
при Т=Т1
(рис. 12, а) визначається з умови
![]() ;
;![]() ,
,
що
графічно інтерпретується у вигляді
загальної дотичної до кривих
![]() і
і![]() (рис. 12, б) у точках
(рис. 12, б) у точках
![]() і
і
![]() .
Аналогічно знаходяться умови рівноваги
.
Аналогічно знаходяться умови рівноваги
![]() при Т=Т2:
загальна дотична до кривих
при Т=Т2:
загальна дотична до кривих
![]() і
і![]() (рис. 12, в) дозволяє знайти концентрації
фаз
(рис. 12, в) дозволяє знайти концентрації
фаз![]() і
і![]() .
.
З цього знаходять точки 2' і 2" на фазовому просторі С-Т діаграми стану.
Аналогічні
побудови можна зробити для будь-якої
іншої температури і таким чином побудувати
криві ТА-1"-ТБ
(ліквідус),
![]() (солідус), а також
(солідус), а також![]() і ТАI
– 2II
– лінії межової розчинності компонентів
Б і А в a-
і b-фазах
відповідно.
і ТАI
– 2II
– лінії межової розчинності компонентів
Б і А в a-
і b-фазах
відповідно.
2.3.3 Діаграма стану з евтектоїдною рівновагою фаз
Якщо у двокомпонентній системі поліморфними є обидва компоненти, то як один з варіантів можлива реалізація трифазної рівноваги евтектоїдного типу (рис. 13, а).
Встановлення
концентрації фаз при двофазній рівновазі
![]() при даній температурі, наприклад Т=Т1,
дозволяє встановити геометричні місця
точок
при даній температурі, наприклад Т=Т1,
дозволяє встановити геометричні місця
точок
![]() і
і![]() ,
які представляють собою криві ліквідусу
і солідусу відповідно.
,
які представляють собою криві ліквідусу
і солідусу відповідно.
Знаходження
точок 1III
і 1IV
загальної дотичної до кривих
![]() і
і![]() (рис. 13, б) і зв’язок їх з точками
рівноважних концентрацій фаз 1I
і 1II
у фазовому просторі діаграми стану є
повністю аналогічним процедурі, що
описана у 2.3.2. Корисно звернути увагу,
що крива
(рис. 13, б) і зв’язок їх з точками
рівноважних концентрацій фаз 1I
і 1II
у фазовому просторі діаграми стану є
повністю аналогічним процедурі, що
описана у 2.3.2. Корисно звернути увагу,
що крива
![]() розташована значно вище, ніж
розташована значно вище, ніж![]() і
і![]() ,
тобто ізобарно-ізотермний потенціалa-фази
є набагато вищим, ніж g-
і рідкої фаз при даній температурі Т1.
,
тобто ізобарно-ізотермний потенціалa-фази
є набагато вищим, ніж g-
і рідкої фаз при даній температурі Т1.
Отже, при Т1 ні при яких концентраціях a-фаза не може бути стійкою.
Для
того, щоб a-фаза
була термодинамічно стійкою, необхідно
знизити температуру. При Т = Т2
(рис. 13, в) нестійкою є вже рідка фаза,
тому що її ізобарно-ізотермний потенціал
перевищує енергію a-
и g-фаз.
Криві
![]() и
и![]() мають загальну дотичну, тобто
мають загальну дотичну, тобто![]() і
і![]() ,
і це показує, що при даній температурі
Т2
обидві фази знаходяться в рівновазі за
умови, що a-фаза
має концентрацію
,
і це показує, що при даній температурі
Т2
обидві фази знаходяться в рівновазі за
умови, що a-фаза
має концентрацію
![]() ,
аb-фаза
-
,
аb-фаза
-
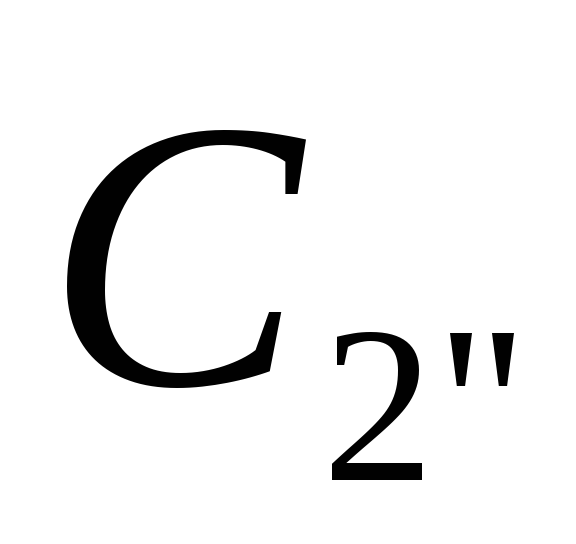 (див. рис. 13, а).
(див. рис. 13, а).
При зміні температури рівноважні концентрації a- і g-фаз змінюються по кривим ТА1-21 і ТАI-2II відповідно.
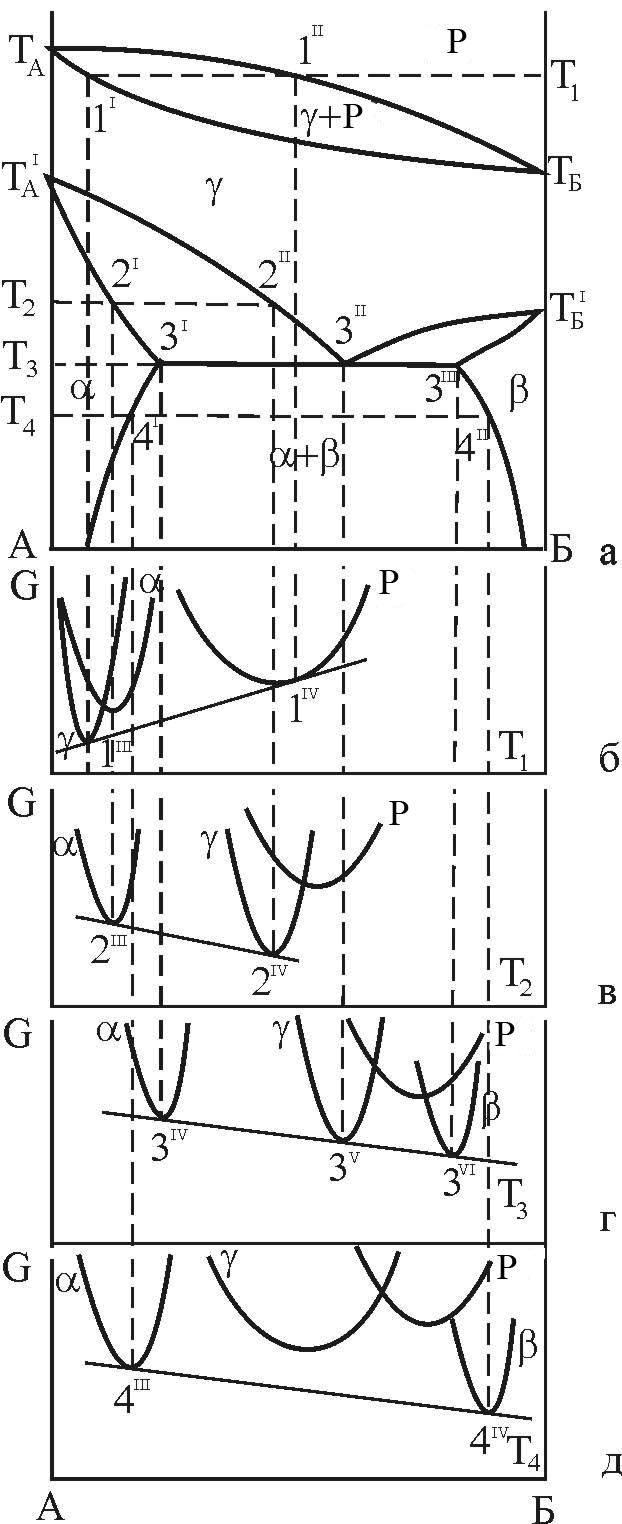
Рисунок 13 – Взаємне розташування кривих ізобарно – ізотермного потенціалу і фазових областей діаграми стану з евтектоїдною рівновагою фаз
Як
виходить з рис. 13, г, при зниженні
температури до Т=Т3
в рівновазі будуть знаходитися три
фази:
![]() ,
причому умова рівності хімічних
потенціалів в усіх трьох фаза накладає
обмеження на склади цих фаз. Вони повинні
відповідати величинам
,
причому умова рівності хімічних
потенціалів в усіх трьох фаза накладає
обмеження на склади цих фаз. Вони повинні
відповідати величинам![]() ,
,![]() і
і![]() дляa-,
g-
і b-
фаз.
дляa-,
g-
і b-
фаз.
При
подальшому зниженні температури,
наприклад до Т = Т4,
криві
![]() і
і![]() розташовуються набагато вище кривих
розташовуються набагато вище кривих![]() i
i![]() і загальної дотичної до цих останніх
(рис. 13, д). Ця обставина робить
термодинамічно нестійкими фазиg
і Р.
і загальної дотичної до цих останніх
(рис. 13, д). Ця обставина робить
термодинамічно нестійкими фазиg
і Р.
Як
і у попередній випадках, загальна дотична
до кривих
![]() i
i![]() (що геометрично інтерпретує рівність
(що геометрично інтерпретує рівність![]() )
демонструє фазову рівновагу
)
демонструє фазову рівновагу
![]() з рівноважними концентраціями
з рівноважними концентраціями
![]() і
і![]() відповідно.
відповідно.
