Глава 2 аналіз діаграм фазових рівноваг у подвійних системах

Аналіз діаграм фазових рівноваг наводиться з метою встановлення:

- фазового складу сплаву даного складу при заданій температурі;

- рівноважної концентрації фаз за даних умов;

- співвідношення мас і об’ємів фаз, що знаходяться у рівновазі за даних умов;

- ступеню свободи системи при даних умов;

- граничних розчинностей атомів компонентів у даній фазі.

Розглянемо докладніше методику проведення аналізу на діаграмах фазових рівноваг кожного типу.

2.1 Діаграми стану з необмеженою розчинністю компонентів у твердій і рідкій фазах

2.1.1 Двокомпонентна система

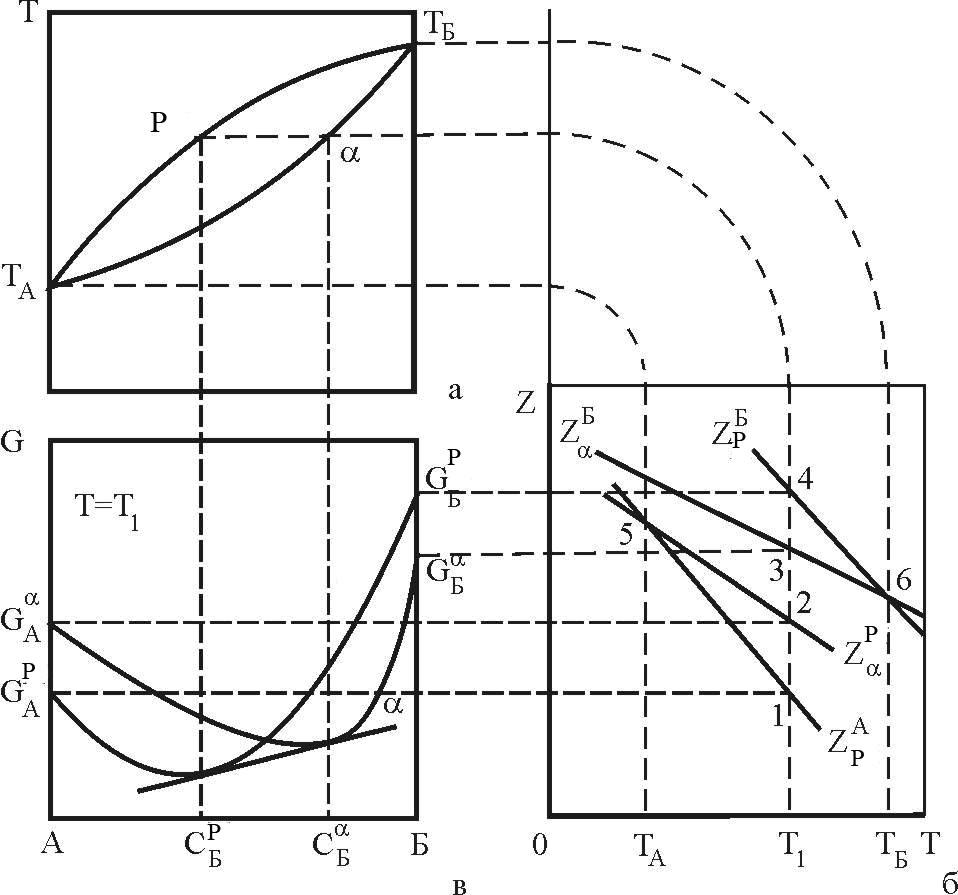
Розглянемо обумовленість взаємних положень фігуративних точок на фазовій діаграмі і кривих мольних вільних енергій чистих компонентів і відповідних подвійних сплавів системи А - Б (рис. 4).

Точка плавлення чистого компоненту А (точка 5, рис. 4, б) знаходиться на перетині кривих мольних вільних енергій рідкої (5-1) і твердої (5-2) фаз цього компоненту. Аналогічно знаходиться точка плавлення 6 компоненту Б.

Отримані точки проектуємо на температурну ось діаграми фазових рівноваг (рис. 4, а) і отримуємо точки Т_А і Т_Б відповідно.

Потім знаходимо на рис. 4, б величини мольних вільних енергій твердої і рідкої фаз чистих компонентів при температурі Т₁. вони визначаються як точки 2, 1, 3, 4 перетину відповідних кривих вільних мольних енергій з ізотермою Т1. спроектуємо отримані чотири точки на ось вільних енергій діаграми G = f(c) - рис. 4, в.

’

Рисунок 4 – Зв’язок кривих термодинамічного потенціалу компонентів, концентраційної залежності вільної енергії фаз з елементами діаграми стану в системі А – Б

Через точки ,,,на рис. 4, в проведемо криві мольних вільних енергій твердої і рідкої фаз подвійних сплавів у припущенні, що однозначно відомий профіль кривих.

Згідно рівняння (16) рівновага твердої і рідкої фаз досягається при рівності хімічних потенціалів атомів компонентів, що утворюють ці фази: і. Тому, щоб знайти величини рівноважних концентрацій співіснуючих фаз при Т=T₁, достатньо у відповідності з рівнянням (12) провести графічне диференціювання, тобто знайти загальну дотичну до кривих і. Точки дотику визначать концентрації фазa і Р, що знаходяться в рівновазі. Спроектувавши ці точки на ізотерму T₁ фазового простору діаграми стану (рис. 4, а), отримаємо точки L₁ і S₁, що належать, як видно на рисунку, кривим ліквідус і солідус відповідно.

Якщо повторити викладена для T = T₁ побудова для більшості інших температур T₂, T₃, … , T_n можна показати, що сімейства точок L₂, L₃, …, L_n і S₂, S₃, …, S_n, побудують криві ліквідус і солідус.

Розглянемо тепер більш докладно деякі геометричні залежності на діаграмі стану (рис. 5).

Виберемо сплав I, склад (концентрація компоненту Б) якого буде описуватися довжиною відрізку . При зміні температури фігуративна точка (нода) буде ковзати по прямій 1-2-3-4.

Як видно на рис. 5, фазовий простір діаграми складається з трьох фазових областей: двох однофазних (області рідкої фази і a-твердого розчину) і однієї двофазної (Р+a).

Таким чином, при T = T₁ сплав I знаходиться в рідкому стані (стійка рідка фаза), при T₃ і T₄ - у твердофазному (стійка a-фаза). При T = T₂ сплав I знаходиться у двофазному стані Р+a.

Для визначення рівноважного складу a і Р, що знаходяться в рівновазі, через точку 2 проведемо ізотерму до перетину з лініями ліквідус і солідус. Цей відрізок в геометричній термодинаміці називається конодою.

Склади фаз, що знаходяться у рівновазі при T = T₂, визначаються абсцисами точок 2^I і 2^II: склад твердої a-фази – відрізком або відрізком, рідкої фази – відрізкомабо відрізком.

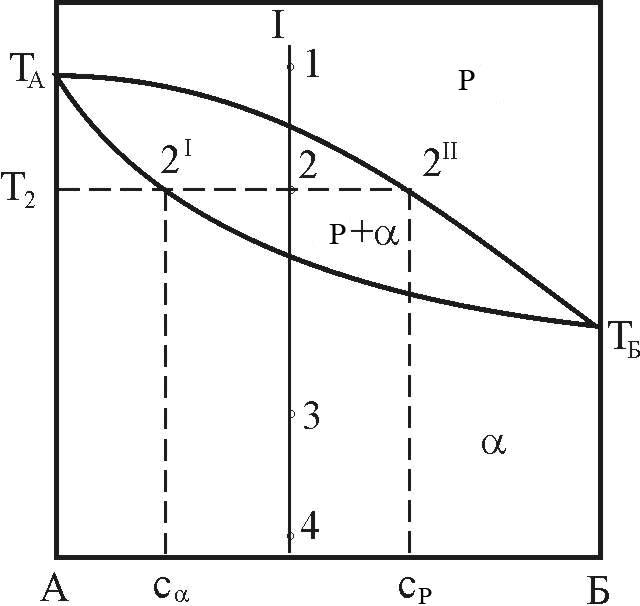
Рисунок 5 – Діаграма стану з необмеженою розчинністю компонентів у рідкій і твердій фазах

За допомогою коноди можна визначити співвідношення мас фаз, що знаходяться у рівновазі при даній температурі. Це можна зробити за допомогою нескладного правила, що іноді (переважно у підручниках старих видань) називають правилом ричага. Сутність цього у наступному: співвідношення мас є зворотно пропорційним відношенню відрізків коноди, на які ділить коноду фігуративна точка, що відповідає складу сплаву.

Наприклад, при Т = T₂ співвідношення мас твердої і рідкої фаз, що знаходяться у рівновазі, зворотно пропорційно співвідношенню відрізків ітобто.

Таким чином, для визначення співвідношення мас фаз слід користуватися шкалою масових відсотків.

Отже, ,,.

Визначення варіантності (ступеню свободи) системи.

Для аналізу ступенів свободи системи при постійному тиску користуються формулою (18).

Отже, для однофазного стану двокомпонентної системи (коли в рівновазі знаходиться одна фаза a або рідка) C=2+1-1=2. Система є двоваріативною.

Якщо у рівновазі знаходяться дві (Р+a) фази, C=2+1–2 = 1, система є моноваріантною.

У випадку рівноваги трьох фаз C=0 (система не має ступенів свободи), вона є нонваріантною.

Визначення межової розчинності атомів компонентів у фазах.

Під межовою розчинністю атомів компонентів у фазах системи розуміють максимальну або мінімальну (або і максимальну і мінімальну) концентрації атомів компонентів у даній фазі, за яких сплав знаходиться ще в однофазному стані.

Наприклад, межова (максимальна) розчинність атомів Б в a-фазі на рис. 5 визначиться лінією T_А – 2^I - T_Б. Насправді, збільшення концентрації атомів Б понад цю величину (наприклад, для Т=T₂ понад ) зсуває фігуративну точку вправо, до області двофазного (Р+a) стану.

З іншого боку, межова (у даному випадку мінімальна) концентрація атомів Б в рідкій фазі виділиться лінією T_Б -2^II -T_A, тому її зменшення зсуває фігуративну точку лівіше за цю лінію і приводить сплав у двохфазний стан. Ця сама лінія може бути описана як лінія межової (максимальної) розчинності компоненту А в рідкій фазі, тому що подальше збільшення концентрації компоненту А в рідині викликає утворення "осаду" - кристалів a-фази, тобто приводить систему у двофазний стан.

Лінії межової розчинності у двокомпонентних системах називають лініями сольвусу.