Операційні системи Зербіно Д.Д. / MMDO3-4

Міністерство освіти і науки України

Національний університет “Львівська політехніка”

Кафедра АСУ

Звіт

до лабораторної роботи № 3-4

Постановка задачі лінійного програмування та її розв’язання симплекс методом

Виконав:

Студент групи КН-22

Карпенко Ростислав

Прийняв:

Балич Б.І.

Львів – 2013

Мета: використовуючи симплекс метод знайти розв’язок задачі лінійного програмування.

Індивідуальне завдання:

Записуємо умову:

F(x₁,x₂) = 2x₁ + 2x₂ 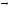max ;

2x₁ + 11x₂ 38,

x₁ + x₂ 7,

4x₁ - 5x₂ 5,

x₁ 0, x₂ 0.

Короткі теоретичні відомості

Симплекс-метод — метод розв'язання задачі лінійного програмування, в якому здійснюється скерований рух по опорних планах до знаходження оптимального розв'язку; симплекс-метод також називають методом поступового покращення плану. Метод був розроблений американським математиком Джорджем Данцігом у 1947 році.

Нехай невироджену задачу лінійного програмування представлено в канонічному вигляді:

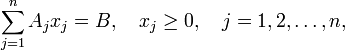
де X = (x1, …, xn) — вектор змінних, C = (c₁, …., c_n), B = (b₁, …, b_m)^T, A_j = (a_1j, …, a_mj)^T, j = 1, …, n — задані вектори, T — знак транспонування, та

відмінні від нуля компоненти опорного плану, для полегшення пояснення розташовані на перших m місцях вектору X. Базис цього плану:

Тоді:

де Z₀ – значення лінійної форми на даному плані. Так як вектор-стовпці матриці A лінійно незалежні, будь який із векторів умов Aj розкладається по них єдиним чином:

де x_ij – коефіцієнт розкладання. Система умов:

z_k ≥ 0, x_j = 0, j = m + 1, …, n, j ≠ k (6)

при заданому k визначає в просторі змінних задачі промінь, який виходить із точки, яка відповідає опорному плану, що розглядається. Нехай значення змінної xk при русі по цьому променю дорівнює θ, тоді значення базисних змінних дорівнюють xi(θ). В цих позначеннях рівняння (5) можна представити у вигляді

помноживши рівняння (3) на θ при j = k та віднявши від рівняння (1),отримаємо

Із рівнянь (7-8) отримаємо

Оскільки xi(θ) при θ = 0 визначають план задачі, то найбільше θ, яке не порушує обмеження xi (θ) ≥ 0, визначається із умови

В силу невиродженості задачі мінімум досягається не більш ніж для одного i = J та θ > 0. Значення лінійної форми при θ = θ0 визначається із рівнянь (9), (4), (2)

де Δk = zk — ck. Очевидно, Δj = 0 для j = 1, …, m

Нехай — початковий базис із m одиничних векторів. Всі дані задачі записуються у вигляді симплекс-таблиці (першої ітерації обчислювального процесу). Симплекс-алгоритм розв'язання задачі лінійного програмування складається із наступних операцій:

1. знайти Δk = min j_Δj. Якщо Δk = 0, тоді план, який розглядається оптимізовано; якщо Δk < 0, вектор Ak вводиться в базис;

2. знайти θ0 та l, для якого , із формули (10). Якщо I = Λ — порожня множина, лінійна форма необмежена зверху; якщо I ≠ Λ вектор Al виводиться із базису;

3. за знайденими l, k обчислити нові значення елементів таблиці за формулами

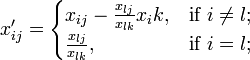
де та перейти до виконання операції (1) з новими значеннями всіх x_ij = x'_ij.

Перетворення (12) замінює вектор коефіцієнтів X_k = (x_1k, …, x_mk) на одиничний вектор X_k з x_lk = 1. В силу монотонного збільшення x0 повернення до вже пройденого плану неможливе, а із скінченності кількості опорних планів випливає скінченність алгоритму.

Початковий опорний план з одиничним базисом можна отримати, розв'язавши описаним алгоритмом допоміжну задачу

при обмеженнях

яка містить одиничний базис, який складається із векторів A_n+1, …, A_n+m.

Цим векторам відповідають штучні змінні із значеннями , i = 1, …, m. Якщо в оптимальному розв'язку цієї задачі , вихідна задача не має розв'язку. Якщо ж та задача невироджена, оптимальний базис складається лише тільки із векторів вихідної задачі, які за формулами (12) перетворені в одиничну матрицю. Якщо задача має невироджені плани, значення z0 може не збільшуватись на ряді ітерацій. Це відбувається через те, що значення відповідних дорівнює нулю та визначається неоднозначно. В таких випадках монотонність методу порушується і може трапитись зациклювання, тобто, повернення до вже пройденого базису. Невелика зміна вектора обмежень задачі, яка полягає в заміні величин b_i на b_i + ε_i, де ε_i достатньо малі, при вдалому виборі εi не змінюють множину векторів оптимального опорного плану вихідної задачі і робить її невиродженою.

Описаний вище алгоритм називається першим (або прямим) алгоритмом симплекс-методу. Також відомий другий алгоритм (алгоритм із оберненою матрицею). В ньому перетворюється лише матриця A^-1, обернена до базисної матриці.

Розвязування задачі за допомогою програми SimplexWin 3.1

Одним зі способів розв’язку задач лінійного програмування є використання прикладних програм, зокрема програми SimplexWin 3.1.

Вводимо дані в програму і нажимаєм кнопку «Вычислить»

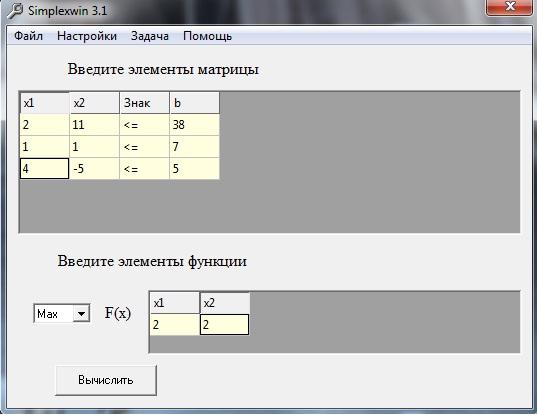
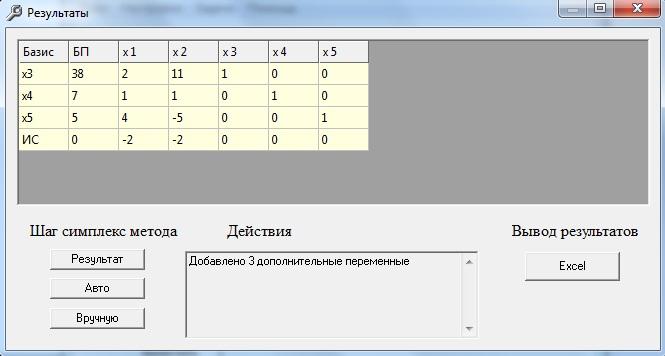
І нажимаємо кнопку «Результат»

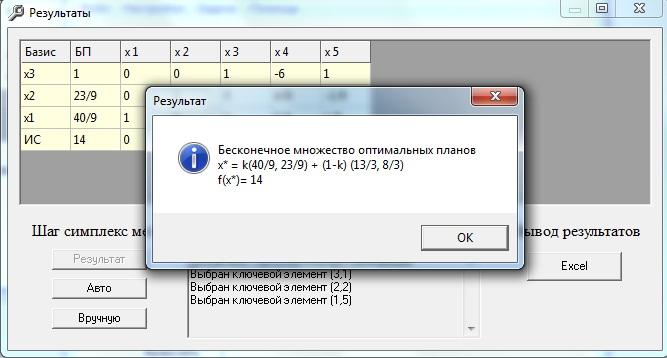
Користування програмою SimplexWin 3.1”

Інструкція користувачеві для роботи з програмою SimplexWin 3.1

Дана програма призначена для рішення задач лінійного програмування симплекс методом.

Основні принципи роботи з програмою:

1. Запускаємо програму SimplexWin 3.1

2. Перед користувачем зявляється головне вікно програми. В ньому користувач повинен вказати розмір вхідної матриці і занести результати.

3. Визначення розмірів матриці.

3.1 Вибираємо Налаштування - Розмір матриці.

3.2 В отриманому вікні встановлюємо кількість рядків і кількість змінних наших обмежуючих нерівностей.

4. Після цього розмір таблиці встановлюється таким, який потрібний користувачеві.

5. В цю таблицю користувач заносить дані.

5.1 На місцях x1, x2, ... ,xn користувач вводить коефіцієнти нерівностей.

5.2 На місцях Знак користувач вибирає знак кожної нерівності.

5.3 В стовпці b користувач вводить значення вільних членів.

6. Нижче під таблицею користувач вводить коефіцієнти цільової функції і вибирає якей вихідне значення він хоче

отримати: Min чи Max.

7. Після цього користувач натискає на ОБЧИСЛИТИ. Отримаємо результат нашого обчислення.

В форму "Результат" додана кнопка "Результат", яка дозволяє виконати обчислення вирішення задачі в автоматичному режимі і показати на екрані лише останню симплексну таблицю і результат. Всі ітерації відображаються в текстовому полі "Виконання".

Додано редактор підпису стовпців, які викликаються відповідною командою з меню "Налаштування". Редактор дозволяє вводити псевдоніми для змінних і правих частин нерівностей. Структура файлу була змінена для збереження інформації про підписи. Тепер останній рядок може мати псевдоніми змінних і правих частин, розмежованих пробілами.

Розв’язання за домогою програми Excel

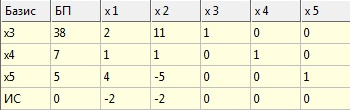
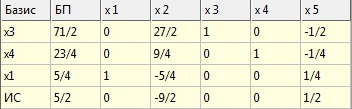
Вибираємо ключовий елемент (2;2)

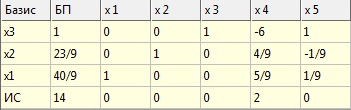
Кінцевий результат:

F(x,y) = 2*23/9 + 2*40/9 = 14

Отже, максимальний результат становить 14.

Висновок: виконуючи дану лабораторну роботу, я навчився використовувати сиплекс метод для розв’язку задач лінійного програмування. Зокрема використав різні програмні пакети для розв’язку симплекс задачі (Excel, SimplexWin 3.1, Mathcad 13).