
- •1. Метричні простори та приклади
- •2. Відкриті та замкнені множини
- •7.Поповнення метричного простору
- •3. Збіжність у метричних просторах
- •6.Неперервні відображення метричних просторів
- •4.Щільність множин
- •5.Повні метричні простори
- •8.Принцип стискаючих відображень
- •9.Відносна компактність.
- •10.Компактні множини в метричних просторах
- •11.Критерій компактності
- •12.Критерій відносної компактності в пр-рі
1. Метричні простори та приклади
М-ну Х
елем. пр-ру дов. природи назив. метричним
простором, якщо кожній парі![]() став.
у відповідність число
став.
у відповідність число![]() так, що вик. умови:
так, що вик. умови:
1.
![]() (аксіома тотожності)
(аксіома тотожності)
2.
![]() (акс.
симетрії)
(акс.
симетрії)
3.![]()
Число
![]() наз.
відст. між елем. х та у, а ф-цію
наз.
відст. між елем. х та у, а ф-цію![]() наз.
метрика.
наз.
метрика.
Метричний
простір – це пара![]()
Якщо на
м-ні Х визначити
![]() і
і![]() ,
то отримаємо різні метричні простори.
,
то отримаємо різні метричні простори.
Приклади
1. Х=R
![]()
Акс. 1,2,3 виконуються.
2.
![]() Елем. пр-ру єn-вимірним
вектори.
Елем. пр-ру єn-вимірним
вектори.
![]()
![]()

Акс. 1,2,3 виконуються.
Доведемо,
що аксіома 3 виконується. Візьмемо
довільне
![]()

Робимо
заміну:
![]()

Для р=1 нерівн. виконується.
Розглянемо
![]()
Використаємо допоміжну нерівність: нерівність Юнга:
![]() ,
,
![]() p,q
– спряжені. Числа спряжені, якщо
p,q
– спряжені. Числа спряжені, якщо
![]() .
.
Доведемо нерівність Юнга.
![]()
Рівн.Юнга
очевидно справедливе, коли а=0 і b=0,
тому розглянемо
![]()

![]()
![]() Площа
прямокутника зі сторонами a
та
b
не перевищує суму площ S1
та
S2
Площа
прямокутника зі сторонами a
та
b
не перевищує суму площ S1
та
S2
![]()
![]()
Нехай




 - нерівність
Гьольдера.
- нерівність
Гьольдера.
![]()
Заст.цю нерівн. для акс.3

![]()
Поділимо
обидві частини нерівності на
 :
:

це нерівн.
справедл. для будь-яких наборів
![]()
Нерівність має назву: нерівність Мінковського.
3.![]()
елем.простору є n-вимірним вектори з дійсними коорд.
![]()
![]()
![]()
4.
![]()
Елем.простору
– послід.дійсних чисел.
![]()
![]() -
збігаються (1)
-
збігаються (1)
![]()
![]() -
збігаються (2)
-
збігаються (2)
 - відст.
визн. коректно, ряд з озн. метрики збіг.
Це випливає з озн. порівн. та збіж.(1) і
(2). Справедл. нерівн. три кут. випливає
з нерівн. Мінковського для рядів.
- відст.
визн. коректно, ряд з озн. метрики збіг.
Це випливає з озн. порівн. та збіж.(1) і
(2). Справедл. нерівн. три кут. випливає
з нерівн. Мінковського для рядів.
5.
![]() - простір обмеж. числ. послід.
- простір обмеж. числ. послід.![]()
![]()
![]()
![]()
![]()
![]()

6.![]() - простір ф-цій неперервних на
- простір ф-цій неперервних на![]() Елем.
про-ру -
Елем.
про-ру -![]() - візнач. на
- візнач. на![]() і
неперервні.
і
неперервні.
![]()
Справедл. акс 1 і 2. Покажемо, що справедл. нерівн. три кут.
![]()
![]()
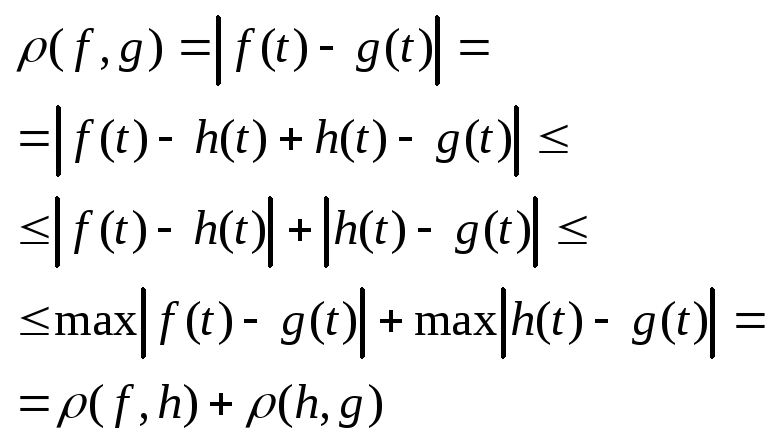
![]()
2. Відкриті та замкнені множини
Нехай Х
– метр. простір.![]() Відкритою кулею з центром у точці х0
радіуса
r
називають множину точок
Відкритою кулею з центром у точці х0
радіуса
r
називають множину точок
![]() таких,
що відстань
таких,
що відстань![]() .
Позначають цю відкриту кулю:
.
Позначають цю відкриту кулю:
![]()
Замкненою
кулею з центром у точці х0
радіуса r
називають
множину точок х
є Х,
таких, що відстань між
![]() .
.
Позначають замкнену кулю:
![]()
Геометрія куль залежить від метрики.
Приклад
1.
![]() Елементами
цього простору є х=(х1,х2)
та у=(у1,у2)
Елементами
цього простору є х=(х1,х2)
та у=(у1,у2)

![]()
Ставиться
задача побудувати кулю
![]()
![]()
![]()
![]()
![]()

2.
![]() Елементами
цього простору є х=(х1,х2)
та у=(у1,у2)
Елементами
цього простору є х=(х1,х2)
та у=(у1,у2)
![]()
![]()
![]()
![]()
![]()

Околом т. хо будемо наз. довільну відер. кулю, яка містить цю точку.
Будемо позначати О(хо)
![]()
Нехай А
– множина у метричному просторі Х,
![]() .
Т. х0
гранична
точка множини А, якщо у будь-якому околі
т. х0
існує
нескінчена множина точок множини А.
.
Т. х0
гранична
точка множини А, якщо у будь-якому околі
т. х0
існує
нескінчена множина точок множини А.
х0 – гранична точка множини А, якщо у будь-якому околі т. х0 міститься хоча б одна точка множини А, яка відрізняється від точки х0
Приклади
1. Х=R A=N
Граничних точок не існує
2. B=R
Кожна
точка множини є граничною.
![]()
Множина А називається замкненою, якщо у неї не існує граничних точок, які їй не належать.
Замиканням
множини А будемо називати множину А до
якої додали всі її граничні точки.
Позначаємо
![]() .
Для замкненої множини А=
.
Для замкненої множини А=![]() .
.
Приклади
Х=R
N-замкнена;
![]() =
N
=
N
Q-незамкнена;
![]()
Нехай А- підмножина метр. простору Х, точка х0, що належить Х називається межовою точкою множини А, якщо у будь-якому околі точки х0 існують точки, які належать множині А і точки, які множині А не належать.
Приклад
![]() Х=R.
Х=R.
А[a,b]
a,b
– межові,
![]()
B(a,b)
![]()
Означення
![]() називається
ізольованою, якщо існує окіл точки х0
в
якому немає інших точок множини А.
називається
ізольованою, якщо існує окіл точки х0
в
якому немає інших точок множини А.
Приклад
Х=R. A=N. Кожна точка ізольована.
А –
підмножина метричного простору Х,
![]() називається
внутрішньою точкою множини А, якщо
називається
внутрішньою точкою множини А, якщо![]()
Множина А називається відкритою, якщо кожна її точка внутрішня.
Приклад
Х=R A=N – замкнена, не відкрита
B=Q – незамкнена, не відкрита
Приклади відкритих множин:
Х- м.п.
![]() -
відкрита множ.
-
відкрита множ.
Х=R
![]() -
відкрита множина
-
відкрита множина
Властивості замикання:
1. Множ.
![]() і
може збігатися
і
може збігатися
2.
![]()
3.
![]()
4.
![]()
