МАТЕМАТИКА(Lek_13-24_1_ivi)

П'ять основних формул Маклорена:

57

Ëåêöiÿ 20. Дослiдження функцiй за допомогою похiдно¨

20.1. Екстремум функцi¨

Теорема 20.1 (достатня умова монотонностi). ßêùî y = f(x) диференцiйовна на

(a; b) i f′(x) > 0 äëÿ âñiõ x (a; b), òî f(x) зростаюча на (a; b); ÿêùî f′(x) < 0 спадна.

Зауваження 20.1. Якщо функцiя зростаюча, то це ще не означа¹ що ¨¨ похiдна додатня.

Наприклад y = x3 зростаюча, але y′ = 3x2|x=0 = 0.

Теорема 20.2 (необхiдна умова екстремуму). Якщо функцiя y = f(x) ì๠â òî÷öi x0 екстремум, то ¨¨ похiдна в цiй точцi дорiвню¹ нулевi (f′(x0) = 0) àáî íå iñíó¹.

Зауваження 20.2. Якщо похiдна в точцi рiвна нулевi, то це ще не означа¹, що там ¹ екстремум.

Наприклад y = x3 â òî÷öi x = 0 екстремуму нема¹, хоча y′(0) = 0.

Означення 20.1. Внутрiшнi точки областi визначення, в яких похiдна функцi¨ дорiвню¹ нулю або не iсну¹, називаються критичними (або стацiонарними) точками.

Теорема 20.3 (перша достатня умова екстремуму). Нехай функцiя y = f(x)

неперервна на (a; b) i x0 (a; b). Якщо при переходi через точку x0 ïîõiäíà çìiíþ¹ ñâié çíàê

з плюса на мiнус, то точка x0 ¹ точкою максимуму, а якщо з мiнуса на плюс, то x0 точка

ìiíiìóìó.

Приклад 20.1. Знайти екстремум функцi¨ y = 25 + 4x3 − x4.Îñêiëüêè

y′ = 12x2 − 4x3 = 4x2(3 − x),

то критичними точкамии ¹ x = 0 òà x = 3.

Зобразимо на рисунку область визначення функцi¨, ¨¨ критичнi точки, визначимо знаки похiдно¨ та поведiнку функцi¨:

Îòæå, ymax = y(3) = −2.

Теорема 20.4 (друга достатня умова екстремуму). Нехай функцiя y = f(x)

визначена на (a; b), x0 (a; b),

f′(x0) = 0, f′′(x0) ≠ 0.

Òîäi x0 ¹ точкою екстремуму, причому якщо f′′(x0) > 0, òî x0 точка мiнiмуму; якщо f′′(x0) < 0, òî x0 точка максимуму.

Теорема 20.5 (третя достатня умова екстремуму). Нехай функцiя y = f(x) визначена на (a; b), x0 (a; b),

58

Приклад 20.2. Знайти екстремум функцi¨ y = x4.

Îñêiëüêè, y′ = 4x3, òî x = 0 ¹дина критична точка. Ма¹мо

20.2. Найбiльше i найменше значення функцi¨ на промiжку

Найбiльше i найменше значення функцi¨ на вiдрiзку [a; b] позначають вiдповiдно

òà min f(x). Цi значення можуть досягатися у точках екстремуму або на кiнцях промiжку.

[a;b]

Приклад 20.3. Знайти найбiльше i найменше значення функцi¨ y = x4 − 2x2 + 5 íà

âiäðiçêó [0; 5].

Ìà¹ìî y′ = 4x3 − 4x = 4x(x2 − 1). Критичними точами ¹ x1 = 0 òà x2,3 = ±1. Оскiльки, iнтервалу (0; 5) належить лише точка x2 = 1, то обчислю¹мо

y(0) = 5, y(1) = 4, y(5) = 580.

Îòæå, max y = y(5) = 580, min y = y(1) = 4.

[0;5]

20.3. Опуклiсть i вгнутiсть функцi¨

Функцiя y = f(x) назива¹ться опуклою íà (a; b), ÿêùî äëÿ äî-

вiльних x1, x2 (a, b) вiдрiзок, що з'¹дну¹ точки (x1; f(x1)) i (x2; f(x2)), розмiщений пiд

графiком цi¹¨ функцi¨. Якщо ж вiдрiзок розмiщений над графiком цi¹¨ функцi¨, то функцiя назива¹ться вгнутою.

y

вгнутою.

Теорема 20.6 (достатня умова опуклостi та вгнутостi функцi¨). Нехай функцiя

y= f(x) двiчi диференцiйовна на iнтервалi (a; b). Òîäi:

1)ÿêùî f′′(x) > 0 íà (a; b), то функцiя вгнута на цьому iнтервалi;

2)ÿêùî f′′(x) < 0 íà (a; b), то функцiя опукла на цьому iнтервалi.

Означення 20.4. Точки, в яких опуклiсть мiня¹ться на вгнутiсть або навпаки називаються точками перегину.

Теорема 20.7 (ознака точки перегину). ßêùî f′′(x0) = 0 i f′′(x) при переходi через точку x0 çìiíþ¹ çíàê, òî x0 ¹ точкою перегину графiка функцi¨ y = f(x).

59

Приклад 20.4. Знайти iнтервали опуклостi i вгнутостi, точки перегину графiка фун-

êöi¨

y = x4 + 2x3 − 12x2 + 3x − 1.

Ìà¹ìî

y′ = 4x3 + 6x2 − 24x,

y′′ = 12x2 + 12x − 24 = 12(x2 + x − 2) = 12(x + 2)(x − 1).

Ðèñ. 20.3.

Îòæå, íà (−∞; −2) òà (1; +∞) функцiя вгнута; на (−2; 1) опукла; x1 = −2 òà x2 = 1точки перегину.

20.4. Асимптоти

Означення 20.3. Пряма назива¹ться асимптотою криво¨, якщо вiдстань мiж ними ста¹ як завгодно малою коли точки криво¨ вiддаляються вiд початку координат.

Розрiзняють вертикальнi та похилi (зокрема горизонтальнi) асимптоти.

ною асимптотою графiка функцi¨ y = f(x).

Приклад 20.4. Графiк функцi¨ y = tg x ма¹ вертикальнi асимптоти x = π2 +πn, n Z. Теорема 20.9. Якщо iснують скiнченнi границi

òî y = kx + b ¹ похилою асимптотою графiка функцi¨ y = f(x).

Якщо обидвi границi скiнченнi лише при x → +∞ (x → −∞), то пряма ¹ вiдповiдно

лише правою (лiвою) асимптотою.

Приклад 20.5. Знайти асимптоти графiка функцi¨

y= 2x2 + x + 3. x − 1

Пряма x = 1 ¹ вертикальною асимптотою, бо

Отже, пряма y = 2x + 3 ¹ похилою асимптотою (лiвою i правою) графiка дано¨ функцi¨.

60

Ëåêöiÿ 21. Функцi¨ двох змiнних

21.1. Поняття функцi¨ двох змiнних

Часто в природi ми ма¹мо залежнiсть того чи iншого процесу чи явища не вiд однi¹¨ незалежно¨ змiнно¨, як S = S(t), а вiд декiлькох, наприклад, m = ρV, S = ab sin α.

Означення 21.1. ßêùî êîæíié òî÷öi (x, y) деяко¨ пiдмножини R2 за деяким правилом f ставиться i вiдповiднiсть певне значення z, òî z називають функцi¹ю двох змiнних i позначають

z = f(x, y).

Множина точок (x, y), â ÿêèõ z = f(x, y) визначена (формула ма¹ змiст) назива¹ться областю визначення функцi¨ f i познача¹ться D(f), а множина значень z областю значень i познача¹ться E(f).

Приклад 21.1. Знайти область визначення i область значень функцi¨

√

z = 1 − x2 − y2.

Областю визначення буде множина точок площини, координати яких задовiльняють

умову

1 − x2 − y2 ≥ 0 x2 + y2 ≤ 1.

Îòæå, D(f) ¹ круг з центром в початку координат радiуса 1. Оскiльки x2 + y2 ≥ 0, òî 1 − x2 − y2 ≤ 1, òîäi

√

0 ≤ 1 − x2 − y2 ≤ 1,

тобто E(f) = [0; 1].

(x, y) → (x0, y0), ÿêùî

( ε > 0) ( δ > 0) : x Uδ(x0, y0) |f(x, y) − A| < ε

i познача¹ться

lim f(x, y) = A.

(x,y)→(x0,y0)

Зауваження 21.1. Òðà¹êòîðiÿ, ïî ÿêié (x, y) → (x0, y0) ¹ довiльною. Якщо рухаючись по рiзних тра¹кторiях отриму¹мо, що функцiя пряму¹ до рiзних чисел, то це означа¹, що

lim f(x, y) íå iñíó¹.

(x,y)→(x0,y0)

Часто перевiрку роблять рухаючись по прямих.

{

61

Зауваження 21.2. Для того, щоб iснувала границя необхiдно, щоб iснували повторнi границi i були рiвнi мiж собою.

21.3. Неперервнiсть функцiй двох змiнних

Означення 21.5. Функцiя f(x, y) назива¹ться неперервною в точцi (x0, y0), ÿêùî

вона визначена в деякому околi цi¹¨ точки i lim f(x, y) = f(x0, y0).

(x,y)→(x0,y0)

Функцiя f(x, y) назива¹ться неперервною на множинi, якщо вона неперервна в кожнiй точцi цi¹¨ множини.

Приклад 21.6. z = x2 + y2 неперервна для всiх (x, y) R2.

21.4. Диференцiювання функцiй двох змiнних

Величина

∆z = f(x + ∆x, y + ∆y) − f(x, y)

назива¹ться приростом функцi¨, а

∆xz = f(x + ∆x, y) − f(x, y) òà ∆yz = f(x, y + ∆y) − f(x, y)

приростами функцi¨ по x òà ïî y âiäïîâiäíî.

Означення 21.6. Границя вiдношення приросту ∆xz äî ∆x ïðè ∆x → 0 назива¹ться

Приклад 21.7. Знайти частиннi похiднi функцi¨ z = x2 sin y + 3.

62

При знаходженнi частинно¨ похiдно¨ по x можна вважати, що y стала, тому

∂z

∂x

= 2x sin y.

Беручи похiдну по y, вважа¹мо x сталою, тодi

∂y∂z = x2 cos y.

21.5. Частиннi похiднi вищих порядкiв

Можна визначити частиннi похiднi другого порядку, зокрема

Аналогiчно визначаються похiднi третього i вищих порядкiв:

Похiднi, якi беруться i по x i ïî y називаються мiшаними.

в точцi разом з деяким ¨¨ околом, то в цiй точцi мiшанi частиннi похiднi рiвнi мiж собою

21.6.Диференцiал функцiй двох змiнних

Çозначення частинних похiдних ма¹мо, що

Означення 21.8. Диференцiалом другого порядку назива¹ться повний диференцiал вiд диференцiала першого порядку.

63

Îñêiëüêè

64

Ëåêöiÿ 22.

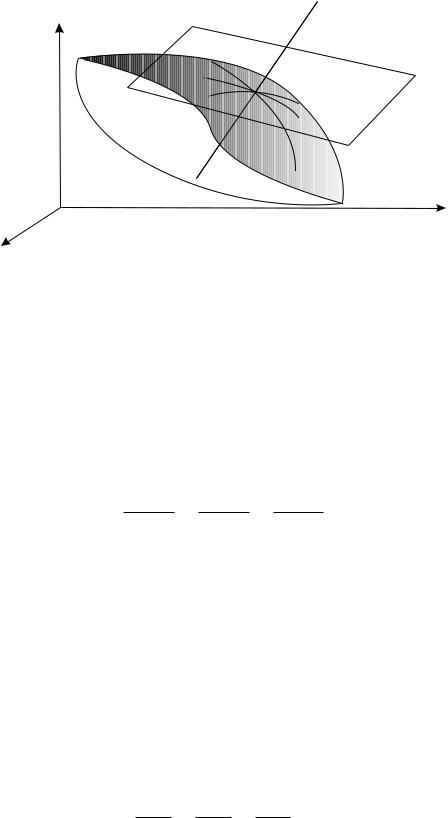
22.1. Дотична i нормаль до поверхнi

Z

M 0

X O Y

Ðèñ. 22.1.

Якщо всi кривi, якi лежать на поверхнi i проходять через деяку точку мають в нiй дотичнi, то геометричне мiсце цих дотичних називають дотичною площиною до поверхнi в данiй точцi.

Пряма, яка проходить через точку дотику перпендикулярно дотичнiй площинi назива¹ться нормаллю.

рiвняння нормалi в точцi M0.

Приклад 22.1. Записати рiвняння дотично¨ площини i нормалi для поверхнi z = xy

âòî÷öi M0(2, 3, 6).

Запишемо поверхню у виглядi

xy − z = 0.

i для точки M0 отриму¹мо вектор {3; 2; −1}. Тому, рiвняння дотично¨ площини

65

22.2. Екстремум функцiй двох змiнних Означення 22.1. Якщо для точки (x0, y0) iñíó¹ òàêå δ, ùî

( (x, y) Uδ(x0, y0)) : f(x, y) < f(x0, y0),

òî (x0, y0) назива¹ться точкою локального максимуму функцi¨ z = f(x, y).

Означення 22.2. Якщо для точки (x0, y0) iñíó¹ òàêå δ, ùî

( (x, y) Uδ(x0, y0)) : f(x, y) > f(x0, y0),

òî (x0, y0) назива¹ться точкою локального мiнiмуму функцi¨ z = f(x, y).

Точки максимуму i мiнiмуму називаються точками екстремуму, а значення функцi¨ в них екстремумом. Функцiя може мати декiлька екстремумiв, а може не мати жодного.

Теорема 22.1 (необхiдна умова екстремуму). Якщо функцiя в точцi ма¹ екстремум, то частиннi похiднi першого порядку в цiй точцi рiвнi нулевi, або не iснують.

Точки, в яких частиннi похiднi рiвнi нулевi або не iснують називаються критичними (або стацiонарними).

Теорема 22.2 (достатня умова екстремуму). Нехай M0(x0, y0) ¹ критичною то- чкою функцi¨ f(x, y), яка ма¹ в цiй точцi неперервнi частиннi похiднi до третього порядку включно, i

Òîäi:

1)ÿêùî ∆ < 0, то в цiй точцi функцiя не ма¹ екстремуму;

2)ÿêùî ∆ > 0, то в цiй точцi функцiя ма¹ екстремум, причому, якщо A > 0, òî ìiíiìóì, ÿêùî æ A < 0 максимум.

У випадку, коли ∆ = 0 функцiя потребу¹ додаткових дослiджень.

Приклад 22.2. Дослiдити на екстремум функцiю

z= x3 + 3xy2 − 15x − 12y.

Знайдемо критичнi точки функцi¨

Отже, критичними точками ¹ M1(1; 2), M2(−1; −2), M3(2; 1), M4(−2; −1). Знайдемо другi частиннi похiднi

zxx′′ = 6x, zxy′′ = 6y, zyy′′ = 6x.

Дослiдимо критичнi точки:

M1 : A = 6, B = 12, C = 6 ∆ = 36 − 144 = −108 < 0;

M2 : A = −6, B = 12, C = −6 ∆ = 36 − 144 = −108 < 0;

M3 : A = 12, B = 6, C = 12 ∆ = 144 − 36 = 108 > 0;

M4 : A = −12, B = 6, C = −12 ∆ = 144 − 36 = 108 > 0.

Îòæå,

zmin = z(2, 1) = −28, zmax = z(−2, −1) = 28.

66