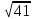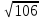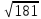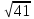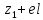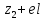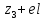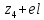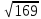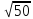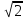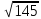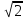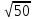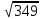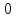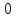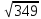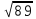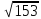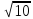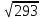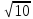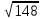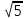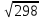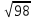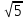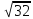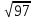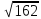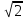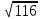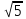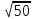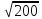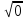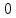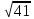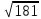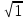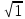РГР_ТА_Яцків_v28
.docxМIНIСТЕРСТВО ОСВIТИ І НАУКИ УКРАЇНИ
Національний унiверситет "Львiвська полiтехнiка"

Розрахункова графічна робота
З курсу теорія алгоритмів
Виконала:
Ст. групи КН-23
Яцків Галина
Львів 2014
Завдання:
-
Здійснити розпізнавання образів із застосуванням евристичного алгоритму порогової величини. Порогова величина Т=2.
-
Здійснити розпізнавання образів із застосуванням алгоритму максимінної відстані.
-
Здійснити розпізнавання образів із застосуванням алгоритму К-внутрішніх групових середніх. К-вибрати за кількістю кластерів отриманих в результаті роботи алгоритму максимінної відстані.
Варіант 3

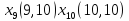
Завдання 1:
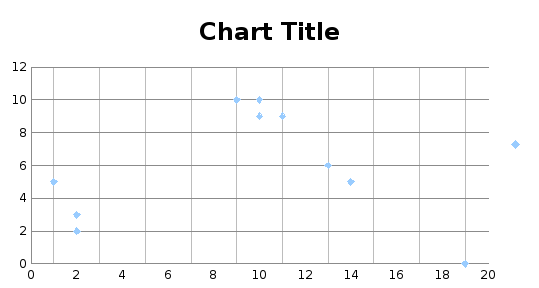
-
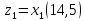 – присвоюємо 1
елементу значення кластера
– присвоюємо 1
елементу значення кластера
-
Тепер рахуємо відстань між кластером до кожного елемента за формулою:
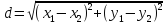
Якщо результат менший за Т , то ми його вносимо в поточний кластер , а якщо більший ,то утворюється новий кластер з координатами поточного елемента.
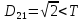 , тому
, тому
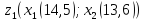
-
Знаходимо відстань від третьої точки до кластеру

 , тому створюємо
ще один кластер
, тому створюємо
ще один кластер
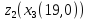
-
Знаходимо відстань від четвертого елемента до кластерів
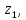

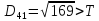
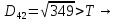 створюємо ще один
кластер
створюємо ще один
кластер
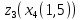
-
Знаходимо відстань від п’ятого елемента до двох кластерів
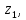
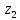 ,
,
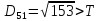
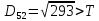
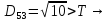 створюємо новий
кластер
створюємо новий
кластер
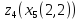
6.Знаходимо
відстань від шостого елемента до
кластерів
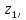
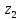 ,
,
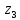 ,
,
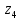
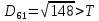
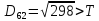

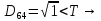 присвоюємо елемент
кластеру
присвоюємо елемент
кластеру
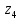

7.Знаходимо
відстань від сьомого елемента до
кластерів
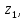
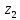 ,
,
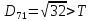
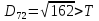
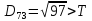

Створюємо новий
кластер
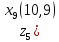
8.Знаходимо відстань
від восьмого елемента до
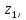
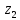 ,
,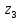 ,
,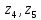
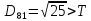
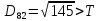
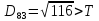
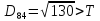
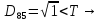 присвоюємо елемент
кластеру
присвоюємо елемент
кластеру
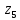
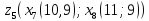
9.Знаходимо відстань
від дев’ятого елемента до
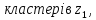
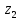 ,
,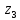 ,
,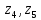
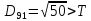
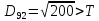
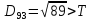
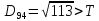
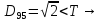 присвоюємо елемент
кластеру
присвоюємо елемент
кластеру

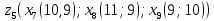
10.Знаходимо відстань
від десятого елемента до
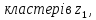
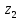 ,
,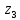 ,
,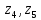
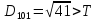
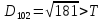
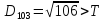
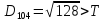
 присвоюємо елемент
кластеру
присвоюємо елемент
кластеру
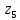
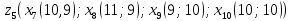
Завдання 2:
-
Беремо довільний елемент , в моєму випадку це перший елемент і присвоюємо значення кластера.
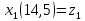
-
Тепер рахуємо відстань між кластером до кожного елемента за формулою:
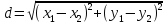
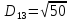
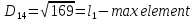
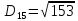
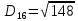

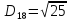
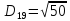
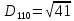
-
З усіх довжин знаходимо максимальний елементом , він стає центром другого кластеру
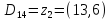
-
Рахуємо відстань від другого кластеру до всіх елементів.
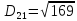

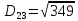
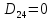

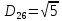


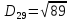
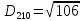
-
Шукаємо мінімальний елемент з результатів знаходження відстаней між 1 кластером і елементами та 2 кластером і елементами. Потім серед мінімальних шукаємо максимальний.
|
|
|
min el |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.Ми маємо перевірити чи виконується умова , щоб зрозуміти чи нам рухатись далі ,чи зупинитись на даному етапі.
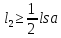
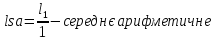
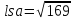
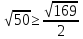
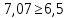
Рівність виконується
, отже
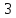 стає третім кластером.
стає третім кластером.
7.
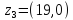
Знаходимо відстань за формулою, яка описана вище:
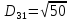
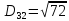
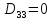
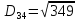
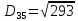

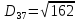
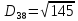
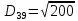
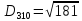
8. Тепер шукаємо min елемент з усіх трьох результатів , а потім max з min.
|
|
|
|
min el |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. Перевіряємо чи виконується рівність :
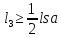
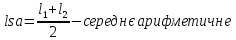
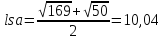
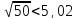
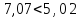
Рівність виконується:
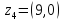

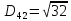

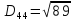

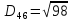

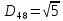
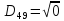
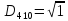
|
|
|
|
|
min el |
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
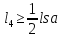
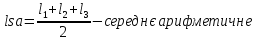
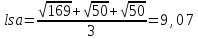
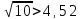

Рівність не виконується . Вийшли такі кластери:
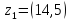



-
К=3 (кількісь кластерів )
Беремо дані із завдання 2 (кластери та відстань від кластерів до елементів).
Шляхом знаходження шляху елементів до різних кластерів утворилися :
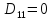
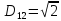
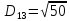
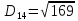
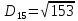
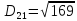
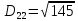


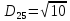

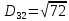
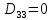
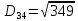
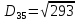
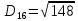
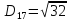

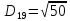
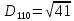

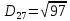
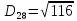


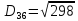
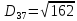
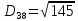

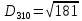
2. Проходимось по рядку і шукаємо мінімальний елемент, потім виписуємо приналежність елемента до кластера :
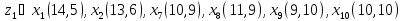
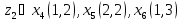
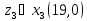
3. Знаходимо середнє арифметичне:
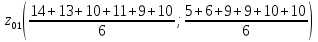 =
(11,2;
8,1)
=
(11,2;
8,1)
 =
(1,7;
3,3)
=
(1,7;
3,3)
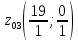 =
(19;
0)
=
(19;
0)
Ці точки стають кластерами. Знаходимо відстань між новими кластерами і елементами.


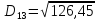
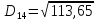
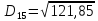


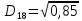
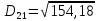

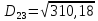
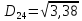
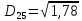
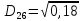


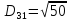
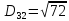
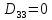
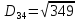

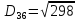
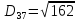
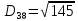
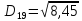
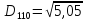
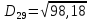
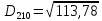

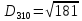

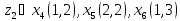

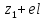
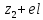
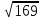
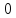
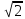
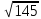
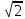
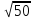
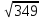
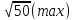
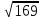

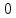
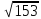

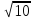
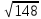

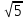
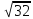
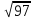
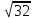
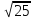


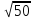
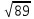
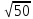
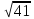

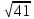
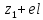
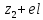


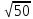
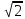
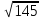
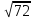
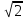
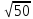

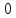
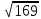
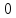
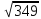
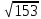
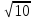
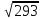
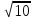
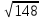
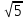
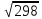

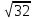

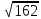

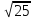
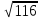



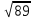
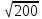
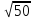 (max)
(max)