
- •5.1 Математичні моделі основних симетричних криптографічних перетворень та їх властивості.
- •5.2 Основні елементарні крипто перетворення симетричного типу
- •Криптографічні перетворення (шифри) типу перестановка
- •Аналітична підстановки в полі Галуа
- •Блочні симетричні шифри та їх властивості.
- •Idea подібні шифри( Європейський стандарт idea та його модифікації і удосконалення);
- •Додаток б Випадкова таблиця підстановки « байт в байт»(Калина)
5.2 Основні елементарні крипто перетворення симетричного типу
1) Афінний шифр [ 3 ].
Твердження
2.7.1 Нехай
 є мова за алфавітом n
і алфавіт мови співпадає з алфавітом
криптограми. Кожному символу відкритого
тексту та гами шифрування поставлене
є мова за алфавітом n
і алфавіт мови співпадає з алфавітом
криптограми. Кожному символу відкритого
тексту та гами шифрування поставлене
 число. Тоді існує афінний шифр з ключем
число. Тоді існує афінний шифр з ключем
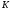 ,
елементами якого є:
,
елементами якого є:
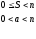 ,
,
якщо
найменший спільний дільник
 .
.
В афінному шифрі зашифровування здійснюється таким чином:
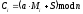 , (2.80)
, (2.80)
а розшифровування:
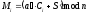 , (2.81)
, (2.81)
де
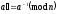 , (2.82)
, (2.82)
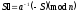 . (2.83)
. (2.83)
Цей шифр є зворотнім.
Доведення:
 обчислюється
за формулою (2.81) з урахуванням (2.82) та
(2.83):
обчислюється
за формулою (2.81) з урахуванням (2.82) та
(2.83):
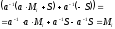 .
.
2) Лінійний шифр.
Твердження
2. Якщо в афінному шифрі
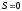 ,
то існує лінійний є взаємо зворотний
шифр, у якому зашифровування здійснюється
як:
,
то існує лінійний є взаємо зворотний
шифр, у якому зашифровування здійснюється
як:
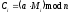 , (2.84)
, (2.84)
а розшифровування:
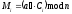 . (2.85)
. (2.85)
3)Адитивний шифр.
Твердження
3. Якщо в афінному шифрі
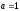 ,
то існує адитивний однозначно зворотній
шифр з правилом шифрування:
,
то існує адитивний однозначно зворотній
шифр з правилом шифрування:
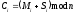 , (2.86)
, (2.86)
 . (2.85)
. (2.85)
доведення здійснюється з урахуванням афінного шифру
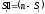 .
.
Симетрія шифру міститься в тому, що ключі поліноміально легко зв’язані і один може бути легко визначений при знанні іншого.
Складання (гамування) символів інформації з ключем чи гамою шифрування за модулем m
Криптографічні перетворення складання за модулем є частковим випадком адитивного шифру згідно(2.86) та (2.87).
Нехай
є мова
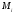 з основою алфавіту
з основою алфавіту
 ,
тоді існує зворотній шифр, який співпадає
з адитивним виду:
,
тоді існує зворотній шифр, який співпадає
з адитивним виду:
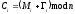 , (2.86)
, (2.86)
 . (2.87)
. (2.87)
Шифр
потокового гамування є випадком афінного
шифру, у якого
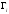 є деяка функція
є деяка функція
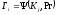 ,
ключа, наприклад (2.65)
,
ключа, наприклад (2.65)
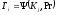 ,
Шифр Вернама
,
Шифр Вернама
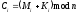 , (2.88)
, (2.88)
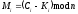 . (2.89)
. (2.89)
На практиці використовується складання за модулем 2:
відповідно для потокового шифру з обчислювальною стійкістю шифру
 , (2.90)
, (2.90)
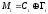 ; (2.91)χ
; (2.91)χ
відповідно для потокового шифру з безумовною стійкістю
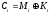 , (2.92)
, (2.92)
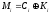 . (2.93)
. (2.93)
-
Криптографічні перетворення (шифри) типу перестановка
Розглянемо відкрите повідомлення М =(М0, М1,…,Мl-1) довжини l з алфавітом Z m. Застосуємо до повідомлення перестановку χ, причому χ ={ χ(0), χ(1),…, χ(l-1}), в результаті отримаємо криптограму { С χ(0), С χ(1),…, С χ(l-1)}. Сімейство таких криптографічних перетворень називають шифром перестановки .
В такій трактовці перестановка є у пере упорядкуванні символів відкритого тексту , що робиться з метою придання криптограмі певного рівня конфіденційності засобом застосування ключа χ.
Розшифрування криптограми С χ(0), С χ(1),…, С χ(l-1) здійснюється засобом застосування до неї однозначно зворотної перестановки χ-1.
Як правило ключ χ використовують певної довжини v, але меншої довжини повідомлення l. За таких умов відкритий текст розбивають на l / v відрізків довжини v, до кожного з яких в подальшому застосовують перестановку згідно ключа χ.
Такий елементарний шифр перестановки має такі властивості.
-
Відносні частоти появи символів в відкритому повідомленні і криптограмі співпадають, оскільки вони інваріантні до перестановки символів тексту.
-
Існують обмеження на довжину ключа v, що використовують.
-
При уже незначних довжинах повідомлення, що зашифровують, необхідно ключ застосовувати багато разів, що спрощує крипто аналіз таких криптограм.
Тому,
як свідчить практика, шифр перестановки
застосовують як елемента

 ечує
криптографічної стійкості.
ечує
криптографічної стійкості.
Історично шифри перестановки у свій час знаходили застосування. Серед них потрібно назвати шифри «скіталa», маршрутні шифри, решето Кардана, подвійної(кратної) перестановки[ 2 - 4 ].
5.3.1Криптографічні перетворення (шифри) типу підстановки( заміни)
Розглянемо знову відкрите повідомлення М =(М0, М1,…,Мl-1 ) довжини l з алфавітом Zsm.
Нехай існує система Ф відображення множини (заміни) Zsm в алфавіт Y шифротексту C, де s – характеристика перетворення заміни, причому
Ф
=
{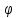 0,
0,
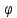 1,
… ,
1,
… ,
 l-1},
(2.95)
l-1},
(2.95)
Значить криптограма С обчислюється по відкритому повідомленню М =(М0, М1,…,Мl-1 ) з використанням відображення згідно ключа Ф, причому Ф виконує функції ключа. За даних умов
С
= (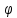 0 (М0),
0 (М0),
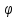 1
(М1),
… ,
1
(М1),
… ,
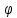 l-1
(М
l-1)
(2.96)
l-1
(М
l-1)
(2.96)
Тепер,
якщо
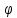 i
є
бієктивним (однозначним) відображенням,
то систему відображення Ф називають
шифром підстановки(заміни).
i
є
бієктивним (однозначним) відображенням,
то систему відображення Ф називають
шифром підстановки(заміни).
В подальшому покладемо, без втрати загальності, що алфавіти криптограм та вхідних символів співпадають, тобто що
Zsm = Y , (2.97)
а
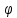 0,
0,
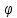 1,
… ,
1,
… ,
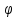 l-1
= підстановки на множині Zsm.
l-1
= підстановки на множині Zsm.
Далі,
якщо прийняти, що
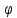 =
=
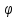 і
для
усіх і = 0,1,
…, l-1,
то
такий шифр є шифром простої заміни(моно
підстановки) на множині Zsm
.
В такому шифрі заміна виконується по
окремим знакам алфавіту. Якщо
і
для
усіх і = 0,1,
…, l-1,
то
такий шифр є шифром простої заміни(моно
підстановки) на множині Zsm
.
В такому шифрі заміна виконується по
окремим знакам алфавіту. Якщо
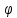 0,
0,
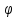 1,
… ,
1,
… ,
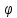 l-1
є
різними, то шифр називають шифром з
багато алфавітної заміни( с).
l-1
є
різними, то шифр називають шифром з
багато алфавітної заміни( с).
Історично шифри підстановки у свій час знаходили застосування. Серед них потрібно назвати шифри Цезаря, Віжінера, латинського квадрату, пропорційної заміни, заміни біграм та s грам [2,195 ].
За
виконання умови (2.97) шифр простої заміни
можна розглядати як
відображенням алфавіту вхідного
повідомлення самого в себе. Для такого
шифру при основі вхідного алфавіту
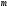 ,
число ключів, тобто різних замін,
визначається як
,
число ключів, тобто різних замін,
визначається як
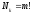 (2.98)
(2.98)
Взагалі шифри простої заміни, навіть починаючи з англійського алфавіту(m = 27), мають великий простір ключів. Але якщо використовується алфавіт натуральної мови, символи якої залежні та нерівно ймовірні, то існують афективні методи крипто аналізу, які отримали назву частотного аналізу.
В суттєвій мірі від такого недоліку вільний шифр полі підстановки. В такому шифрі один вхід і k виходів. Тому для шифру полі підстановки число можливих ключів, з урахуванням (2.98) визначається як
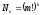 , (2.99)
, (2.99)
де
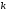 – кількість виходів.
– кількість виходів.
На відміну від шифрів простої заміни, шифри полі підстановки мають багату історію застосування, наприклад у вигляді шифрів колонної заміни. При числі виходів k = 12 та більше отримувані з його використанням шифри мають високій рівень криптографічної стійкості.
На практиці при побудові блочних та поточних шифрів широке застосування знайшли шифри підстановки типу « чотири біти в чотири біти», « байт в байт», рідше «слово в слово»[2,4,9], коли має довжину 16 і більше бітів тощо. Для таких шифрів важливою задачею є побудова таблиць підстановки, які забезпечили б необхідний рівень стійкості. Тому розглянемо декілька прикладів таблиць підстановки.
