3.1.1.9 B-сплайни (2d-вигляд)

Тут основна ідея полягає в ітерованій білінійній інтерполяції. Почнемо з деяких визначень. Нехай – чотири точки в. Гіперболічний параболоїд дозволяє наступне параметричне представлення:

У матричній формі це відповідає

Тепер загальне правило побудови B-кривих виглядає:

Нехай буде (N+1)(N+1) тривимірних точок даних (вимірювання на квадратній сітці) і – два параметри. Після ітераційної лінійної інтерполяції для N-разів з фіксованими параметрамиз

(3-13)

З

В результаті отримана точка – точка на B-поверхні

Примітка: нумерація точок починається з нуля, отже у нас в загальному є (N+1)(N+1) точок даних. Рівняння (3-13) відноситься до всіх координат даних, а саме, х, у, z (див. Приклад 3.1.1.5).

B-поверхня є параметричною і відповідає точціb₀₀ для дляі точцідля. Ця поверхня звивається також поміж інших точок (див. рис. 3.7), які, аналогічно 1D-вигляду, показують кінцеві точки інтерполяції. Полігон, створений на основі точок , називається полігоном Безьє або контрольним полігоном B-поверхні

Існує узагальнення для неквадратних сіток, про які більш докладну інформацію можна знайти в Farin (1993).

Приклад 3.1.1.5 (2D-Вигляд) Розглянемо наступні дев'ять просторових вимірювань на сітках 3 × 3:

Як ми можемо визначити параметричну B-поверхню, яка відповідає цьому набору даних? Ми використовуємо (3-13) для першого кроку білінійної інтерполяції:

(*.1)

Обчислення в (* .1) виконується окремо для кожної координати х, у, z. Наприклад, для першого рівняння в (* 0,1), отримуємо:

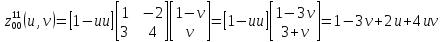
На другому етапі інтерполюємо результати (* .1):

(*.2)

Рис. 3.7 B-поверхня для даних з прикладу 3.1.1.5.

Кінцеві точки позначені зірочками

Параметрична поверхня в (* .2) – шукана B-поверхня, зображена на Рис. 3.7.

Завдання 2.В Нерегулярні інтервали даних (хаотично розподілених вимірювань) інтерполюються (або описуються) з функціональної залежності.

Регресійні підходи, представлені в завданні 2.А залишаються актуальними для 1D- так же як і для 2D-випадку. Детальніше про регресійні підходи в Sect. 3.2.1 і Chap. 4. Структура B-кривих відповідає систематизованим даним та була описана раніше.

Для визначення B-поверхонь потрібен додатковий крок. Почнемо з тріангуляції точок зразка, ця процедура була описана у завданні 2.В.. Після повного покриття області вимірювань може бути виконаний В-сплайнінг. Тут використовуються спеціальні, так звані тріангуляційні B-сплайни.

Причина застосування спеціальних ваг – або параметрів тут – відповідність внутрішній системі координат по трикутнику є аналогічною підходу до білінійної інтерполяції по трикутній сітці, як показано на 3.1.1.3. Наприклад, це дає

для точки на Рис. 3.2. З іншого боку,приймає координати, які

пов’язані з внутрішньою системою координат в трикутнику .

Тепер, сформулюємо загальне правило для побудови тріангуляційних B-поверхонь:

Відповідно до Farin (1993), ми використовуємо скорочення

3.1.2 Стохастична точка зору: Методи геостатистики

Думки про "випадковості" у світі науки відрізняються від твердої віри в абсолютну відмову. Тим не менш, методи, засновані на стохастиці або статистиці, можуть бути підходящими для таких реальних завдань, де математична модель беручи до уваги випадковість здається логічною.

Складні геометричні структури приходять з багатьох областей науки і техніки. Наприклад, геологічні структури, біологічні тканини, ділянок пористого середовища і нафтові родовища часто вимагають статистичного аналізу. Є різні математичні області, які забезпечують такі моделі та методи. Одина з них називається геостатистикою.

У 1950 геостатистика стала швидко розвиватися як галузь прикладної математики і статистики, починаючи з гірської промисловості, а її методи були спочатку розроблені поліпшити розрахунки рудних запасів. "Крігінг", який є спільним терміном для різних методів інтерполяції в геостатистиці, названий в честь Д.Г. Krige, гірничого інженера, який разом з статистиком H.S Sichel, був серед початківців в цій галузі досліджень. Обидва вони працювали в Південній Африці на початку 1950. Пізніше в цьому десятилітті центр геостатистичного досліджень переїхав до Франції, щоб Комісаріат де l'Energie Anatomique. Геостатистика отримала статус наукової дисципліни завдяки роботі Г. Matheron, який удосконалив методи Krige, він увів так звану регіоналізіровану змінну, і розроблені основні поняття теорії оцінки ресурсів.

У 1970-х роках ці поняття геостатистики стали відомі в інших галузях наук про Землю. Вони популярні в промисловості а також в економіці, тому що є проблеми, які необхідно оцінити у часі та просторі - іноді просторово-часовому розподіленнні і навіть корельованні даних.

Проте, методи лінійної геостатистики були насправді не зовсім новими в математиці. Теорія оцінювання в статистиці включала знайомі методи. "Розміщення " від геодезії і класичний аналіз регресії також популярні. Ці методи засновані за методом найменших квадратів, розробленого великим математиком Гауссом, і згодом вони були адаптовані до різних областей досліджень для широкого кола проблеми формулювання зустрічається на практиці. Тим не менше, проблема вибору – один, який є більш філософським і менш математично віддалений: вибір робочого простору, з первинних припущень, і точки зору.

В даний час, геостатистика охоплює різні моделі і методи. Крім того, завдяки останнім подіям з математичної статистики та чисельного аналізу, а також як краще і швидше комп'ютерів, їх кількість продовжує зростати. У цій книзі ми запропонували короткий огляд основних понять і представили типові програми деяких методів Крігінга. Для більш детальної інформації про геостатистику ми рекомендуємо книгу Г. Wackernagel (1995). Почнемо з деяких важливих визначень в геостатистиці.

Ми припускаємо, що читач має деякі фундаментальні знання стохастики, знайдені, наприклад, в K.L. Чунг (1968).

Визначення 3.1.2-1 {Z (х)}, х ∈ Rn називається випадковим полем, якщо Z (х) є випадковою величиною для кожного х ∈ Rn. Якщо х = т ∈ R ⇒Z (т) можна назвати випадковим процесом.

Визначення 3.1.2-2 відокремлює реалізацію {г (х)}, х ∈Rn випадкового поля {Z (х)}, х ∈ Rn, називається районовані змінна.

Різниця між термінами «випадкового поля" і "регіоналізації змінної" можна легко пояснити. Киньте монетку три рази. Якщо її сторони позначені 1 і 0, тобто наступні вісім можливих реалізацій цього випадкового процесу (для дискретної шкали часу, відповідний кожному кидку): [0, 0, 0], [0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1], [1, 0, 1], [1, 1, 0] і [1, 1, 1]. Але ми отримуємо тільки один з цих реалізацій. Регіоналізована змінна з цього процесу є лише одним з цих реалізацій.

Визначення 3.1.2-3 Наступне рівняння називається кореляційною функцією випадкового поля {Z (х)}, х ∈ Rn:

Примітка: коваріаційна функція є вектор-функція, яка залежить від багатьох змінних. Середнє значення випадкової величини, відповідно, тобто результат випадкових відмінностей, позначається Е у визначенні 3.1.2-3. Для спрощення наступні два припущення мають бути зроблені:

1. По-перше, порядок стаціонарності: EZ (х) = EZ (х +) = μ = Const. Це означає, що середнє значення випадкового поля є постійним і, що середнє значення те ж саме в будь-якій точці області.

2. По-друге, порядок стаціонарності: С (х, ч) = С (| ч |). Це означає, що коваріації між будь-якою парою місць залежиать від довжини вектора відстані h, що відокремлює їх. У цьому випадку кореляційна функція є функцією однієї змінної, залежної тільки від відстані; Тому, другий порядок стаціонарності виключає напрямки ефекти.

З практичної точки зору кореляційна функція впливає на оцінку таким же чином, як функції впливу описані в п. 3.1.1. Але є і більш складні умови для її будівництва [см Яглом (1986) для більш докладної інформації].

Визначення 3.1.2-4 Нормована функція коваріації називається кореляційною функцією.

Визначення 3.1.2-5 Для випадкових величин Z1 = Z (x1) ,. , , , Zn = Z (Xn) наступна матриця називається коваріаційною матрицею.

Основна концепція стохастичної інтерполяції широко відповідає детермінованій інтерполяції, використовуючи функцію впливу. Таким чином, у нас є, щоб відповідати середньозваженої урахуванням інформації від місця розташування точок регіоналізації змінної, щоб отримати оцінку певного значення у фіксованій точці (х0, у0), або, загалом, х0.

Ця основна ідея може бути пояснено за допомогою простого прикладу. Нехай [Z (x1, y1), Z (x2, y2)] буде регіоналізованою змінною, яка може, наприклад, бути результатом двох свердловин з нафтового родовища. Або думати про виміри, для параметрів, наприклад, температури або грунту. Тим не менш, ми шукаємо вагу, WI, я = 1, 2, передбачивши в точці (х0, у0). Як ідея узагальненого середнього з п. 3.1.1, це означає, що

Ці ваги, αi, i = 1, 2, повинні залежати від відстані до точки прогнозу: ближче точки повинні мати більш сильний вплив на точність прогнозування. Оцінка вказується в «шапці», Z (х0, у0), для того, щоб відрізнити її від істинного, але невідомого значення випадкової величини Z (x0, y0). В якості запобіжної "близькості" цієї оцінки до істинного значення, ми можемо використовувати

Дисперсію випадкового вектора в квадратних дужках можна розуміти тут у такому сенсі, як його "стохастичну довжину." З вступом першого порядку стаціонарності, ми можемо припустити, що середня цього вектора дорівнює нулю. Але, звичайно, є багато різних випадкових векторів, які виконують це припущення. Мінімізація дисперсії, обмежує клас цих векторів і прагне отримати значиму оцінку. Процедура оцінки повинна ґрунтуватися на знанні коваріацій серед випадкових величин в різних точках.

З розрахованими параметрами використання коваріації моделі

Різниця в (3-18’) є функцією N змінних, тобто, необхідна вага. Після часткового диференціювання цих ваг, ми отримуємо

І в кінці-кінців

Рівняння (3-19) утворюють суму, що в матричному вигляді відповідає

Очевидно, що рішення суми (3-19) Приводить безпосередньо до ваг, що ми шукаємо. Якщо ми позначимо ці ваги [a1^l,…an^l]. Tо потім отримуємо

На додаток до прогнозованих значенням z, ми також отримати так звану дисперсію Крігінга, точність вимірювання сильно залежить від обраної моделі. Враховуючи (3-18) з вагою від (3-19) отримаємо

Якщо місця вимірювання розкидані нерівномірно в просторі варто щоб робити карту Крігінга дисперсії в якості доповнення до карти.

За нашими оцінками або оцінками Крігінга. Це дає нам оцінку зміни точності з оцінками Крігінга, які через неправильні в певних місцях значеня можуть змінюватися.

Тепер давайте перевіримо, як простий крігінг працює на прикладі.

Приклад 3.1.2.1 Ми використовуємо наступні значення із змінної регіоналізації г (0, 0.2) =1, z (1.2, -0.9) = -3, а також вважатимемо, що E (Z) = μ = 2 відомі. Ми визначаємо модель, а потім знаходимо оцінки в точці (х0, у0) = (0, 0) у вигляді

Першого порядку стаціонарності відповідно:

Дисперсія повинна бути зведена до мінімуму:

Тепер у нас є все необхідне, щоб мінімізувати функцію (ПКТ) двох змінних. Інші параметри незмінні. Таким чином, отримаємо

або в матричній формі

Як було зазначено вище, модель для коваріаціонної функції С (Н) задана. Ми розраховуємо всі відомі матричні елементи в (* 0,4) наступним чином:

Рішення [a1^L a2^L]^T залежить від вибору моделі. З ваг, отриманих з (* 0,4) оцінки, відповідно

Крігінг дисперсія розраховується шляхом

Примітка: модель для коваріаціонної функції повинна бути заснована на емпіричній коваріації. Функція розраховується із заданими значеннями регіоналізації змінної.

Є деякі класи моделей коваріаціонних функцій, які можна розрізняти в залежності від моделі коваріації, ми можемо застосовувати параметри моделі на нелінійних методах регресії. Але часто геомтатисти обмежують себе лише оптичною підгонкою. Замість кореляційної функції ми можемо використовувати іншу модель функціональну - добре відому в геостатистиці і навіть більш популярну так звану варіограму.

Варіограма

Визначення 3.1.2-6 Нехай {Z (х)}, х ∈ Rn це випадкове поле. Наступна функція називається варіограммою випадкового поля:

На відміну від визначення (3.1.2-3) коваріаціонної функції, визначення (3.1.2-6) не використовує будь-якої інформації про середнє випадкове поле. Таким чином, ця функція цікава для широкомасштабного класу випадкових полів. Ми припускаємо, що це "невидиме середнє" ідентичне для будь-якої області поля

Визначення 3.1.2-7 Якщо варіограмма випадкового поля залежить тільки від довжини вектора зсуву, поле називається нерухомою характеристикою, що означає, що

Деякі властивості варіограми з власним стаціонарним полем це:

Ми обговорюємо тільки внутрішні стаціонарні поля в цьому розділі, тому ми будемо використовувати короткі позначення γ (h) для γ (| h |). Крім того, якщо середні випадкові поля відомо, то EZ (х) = μ = Const, наступні співвідношення в варіограмі і коваріації функціі будуть:

Тепер ми представляємо деякі моделі варіограмм і обговоримо можливі шляхи їх визначення. Очевидно, що багато програмні засоби, розроблені для геостатистики включають в себе автоматичні інструменти для їх установки. Для читачів, які хочуть зробити більше, ніж натиснути кнопку, ми пояснюємо, як модель може бути визначена. Установка функції кореляції після установки варіограми це - проста модель. Зверніть увагу, що друге співвідношення з (3.21) може бути застосовано.

Насправді іноді потрібно узагальнення існуючих математичних моделей.

Одне з таких узагальнень, так званий ефект самородка, послаблює властивість варіограмм (1)

Поведінка в дуже невеликих масштабах, недалеко від утворення варіограм, має важливе значення, а це означає, тип безперервності регіоналізації змінної: диференційована неперервною лінією а диференційована переривчастою. Якщо варіограмма НЕ диференційована на початку, це “симптом самородка” вплив позначення, що стається через золоті самородки, які містяться в деяких зразках. Ці самородки мають природну ширину, що призводить до того, що значення змінної змінюється різко. Тут ми обговоримо обидва види моделей: без урахування “самородного ефекту”, який позначимо через пе. Введемо наступні моделі: потужність варіограми, експоненціальна група варіограм, варіограма Гаусса, сферична варіограма, і варіограмма з білим шумом. Параметр б зазвичай називають порогом. З (3.21) видно, що дисперсія випадкового поля відповідає γ (∞), так як С (∞) = 0. Таким чином, дисперсія випадкового поля без самородного ефекту відповідає нижній межі дисперсії полів з “самородним ефектом” і є сумою нижньої межі і “ефекту самородка”, що є B + пе. потужність варіограмм

Без “ефекту самородка” (див 3.8.)

З “ефектом самородка”:

Рис. 3,8 Потужність варіограмм без “самородного ефекту” для параметрів р = 0,5, 1,0 і 1,5; б = 1

Примітка: При р = 1 варіограма має потужність від 3-23 () до (3-23?) Називається також лінійною варіограмою. Рівняння (3-21) не вірне для данної варіограми бо вона збільшується до нескінченності.

Експоненціальна сім'я варіограм

Без ефекту самородка (див 3.9.)

З ефертом самородка:

Примітка: При р = 1 варіограма з (3-24) і (3-24) називається експоненційною

варіограмою. Для р = 2 ми отримуємо варіограмму Гаусса. Рівняння (3-21) вірні і існують функції коваріації всферичній варіограмі

Ця модель варіограми часто застосовуются в практичних розрахунках.

Рис. 3.9 варіограма від експоненціального сімейства без “самородного ефекту” для параметрів р = 0,5,

1,0 і 2,5; = 10; б = 1

Без ефекту самородка (див 3.10) .:

Рис. 3.10 Сферичні варіограми без “самородих ефектів” для параметрів а = 1, 5, 10; б = 1

З “самородним ефектом”:

Варіограма “білого шуму”

Це модель чистого “самородного ефекту”. Вимірювання (Z-значення) НЕ

корелюються. Прогнозувати використання стохастичного впливу між точками неможливо.

В цьому випадку слід використовувати детерміновані підходи, описані в п. 3.1.1.

Варіограма “Хмара” та модель “Місце”

Теоретичне визначення варіограм (3.1.2-6) заснованих на парах випадкових значень. Визначення варіограм починається з оцінки вибіркових пар:

Виміряні значення розраховуються і в результаті невідповідності γ * (вертикальна вісь) нанесені проти поділу обраних пар на основі відстані

між локаціями J (горизонтальна вісь), що утворюють хмару варіограмм (див рис. 3.11a). Крім того, ця хмара нарізаних класів розділена в просторі.середні невідповідності в кожному класі утворюють послідовність значень для експериментальних варіограм, що показано на рис. 3.11b. Ці невідповідності часто збільшуються з відстанню, Ці зразки близькі один до одного або навіть однакові. Хмара варіограмма сама по собі може розглядатися як потужний інструмент для вивчення особливості просторових даних. Розподіл вимірювань, аномалії і неоднорідностей можуть бути виявлені даним шляхом. Дивлячись на поведінку відмінностей на коротких відстанях, ми можемо зробити припущення про “ефект самородка”. В деяких

випадках, внаслідок наявності винятків, варіограмана хмара складається з двох окремих хмар.

Будівництво експериментальної варіограми аналогічне звичайній гістограмі.

Рис. 3.11 Хмарна (a) та емпірична (b) варіограма для простих даних, взятих з Прикладу 3.1.2.1; (с) лінійна варіограма, як модель варіограми для прикладу 3.1.2.2.

Зауваження: Враховуючи визначення (3.1.2-8) нам необхідно пояснити «важку форму» цього визначення. Знаменник враховує число пар, що розташовані в субінтервалах. Функція l, що використовується зазвичай в просторовій статистиці і вказує на наступне:

Означення 3.1.2-9 Варіограмна модель задовільняяючи умову

може використовуватися як оцінювач істинної, але невідомої варіограми випадкового поля.

Ця процедура мінімізації пов’язана з усіма модельними параметрами. Деякі варіограмні моделі були представлені вище.

Приклад 3.1.2.2 Ми розглядаємо вимірювання, розташовані поверх профілю:

Варіограма хмара має зв’язок з шістьма ймовірними віддаями: hij = 0,1,2,3,4,5. Покажемо поетапно обчислення хмарної і емпіричної варіограм (див. Рис.3.11a, b):

Віддаль, hij	Варіограма хмара з (3-27)	Емпірична варіограма з (3-28)
0	Шість пар прямують до 0	0
1	П’ять пар з координатами (0,1), (1,2), … (4,5) прямують до:	Арифметичний зміст значень в лівій колонці прямує до значень емпіричної варіограми для інтервалу (0, 1]:
2	Чотири пари з координатами (0, 2), (1, 3), … (3, 5) прямують до:	Арифметичний зміст значень в лівій колонці прямує до значень емпіричної варіограми для інтервалу (1, 2]:
3	Три пари з координатами (0, 3), (1, 4) і (2, 5) прямує до:	Арифметичний зміст значень в лівій колонці прямує до значень емпіричної варіограми для інтервалу (2, 3]:
4	Дві пари з координатами (0,4) і (1,5) дають	Аналогічно:
5	Остання пара (0,5) прямує до:

Тепер пристосовуємо емпіричну варіограму до варіограмної моделі. Щоб спростити варіограму. Щоб спростити вираз вибираємо лінійну варіограму з ефектом самородку [див. (3-23`)] для p = 1. Таким чином, шукаємо параметри ne, b:

Це класична проблема типів лінійної регресії, що описувалась в розділі 3.1.1.

Використовуючи (3-9) отримаємо:

Тут приймемо h1 = 0, h2 = 1 … h6 = 5 і використаємо значення емпіричної варіограми, обчисленої в таблиці вище. Таким чином, ми підставляємо дану лінійну варіограмну модель в емпіричну варіограму (див. Розділ 3.11с):

Слід зауважити, що ця варіограмна модель не прямує до ідеальної відповідності, тому що ефект самородку є надто великим. Позаяк, це лише навчальний приклад для кращого розуміння означень.