3.3.2 Точки і знаки: Парна і точкова кореляційна функція і точковий процес статистики.

Теорія точкових процесів, теорія відзначених точкових процесів і стохастична геометрія відносно нові математичні методи, які займаються стохастичними моделями для просторово розподілених параметрів чи змінних. Зокрема, такі моделі пропонують деякі ефективні підходи, які можуть бути застосовані в матеріалознавстві, геології, біології, лісовому господарстві та інших галузях з дискретними просторовими структурами.

Точковий процес - математична модель для опису випадкового точкового шаблону. Детально описали теорію точкових процесів Каленберг (1986), Карр (1986), і Стоян (1994). Надалі ми надаємо деякі корисні визначення і пояснюємо відповідні приклади.

Міра інтенсивності описує середню кількість випадкових точок у множині в Евклідовому просторі. Для додатків, обговорюваних нижче ми обмежимося випадковим точковим процесом на площині. Для стаціонарних і однорідних точкових процесів міра інтенсивності відповідає

Λ (B) = λ • ν (B) (3-92)

де ν (B) це площа групи B і λ - це середня кількість точок у частині площі, яка називається інтенсивністю. Так звані характеристики другого порядку відіграють важливу роль в теорії зазначених процесів. Кожна точка в зазначеному точковому процесі отримує знак, який характеризує її якимось чином. Наприклад, нехай точковим процесом буде опис місця дерев у лісі. Деякими корисними ознаками, що описують дерево є його висота, вік і діаметр на рівні грудей.

Ми почнемо з наступного вимірювання, яке описує середнє функції f приймаючої значення пар випадкових точок, розподілених у двох сетах B₁ і B₂:

Α_f⁽²⁾ (B₁xB₂)=E ∑ ∑ f (m₁, m₂) 1_B1 (x₁)1B₂ (x₂),

[x₁,m₁]ЄΨ [x₂,m₂]ЄΨ

x₂≠x₁ (3-93)

t=x₁, x₂

Якщо функція щільності ρ_f⁽²⁾ (x₁,x₂) вимірювань (3-93) існує, то вона називається f- продукт щільності, і

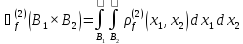(3-94)

більш зручним для користувачів є опис значень f- продукту щільності ρ_f⁽²⁾ (x₁,x₂) що полягає в наступному: Розглянемо два в нескінченно малих диски з центрами у випадкових точках x₁ і x₂ і з площами dF₁ і dF₂. Ми визначаємо випадкову величину, що приймає значення f(m₁,m₂), якщо хоча-б тільки одна випадкова точка знаходиться в кожному з цих дисків. В іншому випадку це випадкова величина приймає значення нуль. Тоді середнє цієї випадкової величини ρ_f⁽²⁾ (x₁,x₂)dF₁dF₂.

Точковий процес називається ізотропним, якщо вірно наступне:

ρ_f⁽²⁾ (x₁,x₂)= ρ_f⁽²⁾(r), r=‖x₂-x₂‖ (3-95)

Рівняння (3-95) означає, що щільність f- продукту залежить від відстані між точками, а не від їх просторового розташування. Останньою, але не менш важливо, характеристикою другого порядку є так звана знакова кореляційна функція k_f(r), яка визначається як

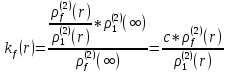
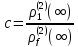, ρ₁⁽²⁾ (r)≠0, (3-96)

ρ₁⁽²⁾ (r)= ρ_f⁽²⁾ (r) mit f(m₁,m₂)=1

Функція ρ₁⁽²⁾ (r) в (3-96) називається парною кореляційною функцією. Є різні оцінки щільності f- продукту, і вони, як правило, мають наступну форму:

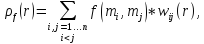
(3-97)

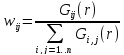
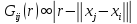
де знак ∞ означає "пропорційно до". Кількість точок в реалізаціях точкового процесу позначається n. Стоян і Стоян (1992) пропонують використовувати наступні ваги Gij (r):

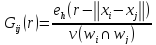
(3-98)

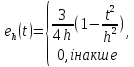-h ≤ t ≤h

В (3-98) використовується так звана ​​Епанечнікова функція e_h(t). Вибір вікна W і параметра h обговорюється в Стоян і Стоян (1994). Як правило, перший тестує різні параметри, поки значущих результатів не отримано. Альтернативні ваги знаходяться так

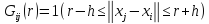(3-99)

Це подання ваг в основному застосовується для розрахунку звичайних гістограм, та оцінки щільності f- продукту з вагами з (3-99) може використовуватись в якості спеціальних узагальнених гістограм.

Звичайні форми функції f є наступними

а) f(m_i ,m_j)=m_i*m_j,

(3-100)

b) f(m_i ,m_j)=׀m_i*m_j, ׀

де m_i, i = 1 ... n являє собою параметр або знак, відповідний точці x_i, i= 1 ...n. Оцінка знаку кореляційної функції може допомогти нам проаналізувати взаємодію між точками всередині точкового процесу. Знову ж таки, будемо думати що точковий процес задається позиціями дерев. Якщо сусідні дерева підтримують один одного, знак висота дерева може зайняти відносно великі значення в кожній точці. У разі придушення одне високе дерево впливає на ріст навколишніх дерев, що призводить до малих значень знака. Якщо формула (b) з (3-100) використовується, то можна розглянути наступну оцінку кореляційної функції знаку:

(3-100’)

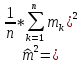
з ρ_f (r) з (3-97).

Примітка: Форми (a) і (b) з (3-100) стоять в різних ситуаціях, які повинні бути проаналізоавані. Наприклад, (а) призводить до "загального впливу" знаку залежного від відстані між відповідними точками. Відстань r з локального мінімуму ρ_f (r) являє собою так звану «негативну взаємодію" між мітками. Або, іншими словами, середній результат обох знаків на такій відстані зменшується. В протиставлення цьому, відстань r з локального максимуму ρ_f (r) являє собою " позитивну взаємодію "між параметрами. Форма (b) призводить до локальних мінімумів ρ_f (r) в місцях з приблизно однаковими або близьких по значеннями. Локальні максимуми відповідають місцям зі збільшенням різниці між мітками.

Такі інтерпретації повинні бути оброблені з обережністю, тому що є також чисельні ефекти, створювані в процесі оцінки. Перевага полягає в тому, що оцінка (3-97) може бути застосована з або без будь-яких припущень про випадковість розташування точок. У детермінованих випадках ця оцінка може бути інтерпретована як єдина для параметра впливаючої функції.

У прикладі 3.3.2.1 ми показуємо в більш докладно, як оцінка знаку кореляційної функції може бути виконана.

Приклад 3.3.2.1 (продовження нижче) Розглянемо наступну зазначену точкову модель з n = 76. Знову ж таки, подумаємо про місця дерев, тобто координати (x, y). Відмітка m визначена для діаметра дерева на висоті грудей (DBH) в сантиметрах:

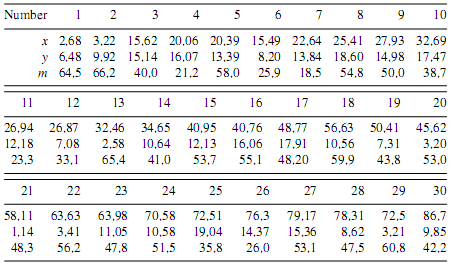
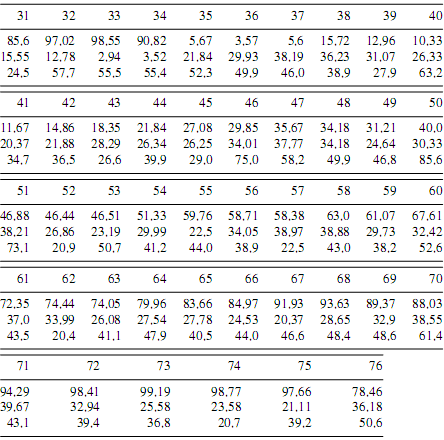
Діаграма 3.34 наводить дані для оглядового вікна. Значення m⁽²⁾ з (3-100’) розраховується наступним чином

m⁽²⁾=(1/76(64,5+66,2+….+39,2+50,6))²=2042 (*,1)

Перед функцією знаку кореляції k_f (r) з f (m_i,m_j) = m_i*m_j ,i ,j = 1... 76 оцінюється, матриця відстаней

(d_ij)_I,j=1…76,

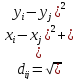
повинна бути визначена. Після поділу R-осі, на рівні інтервали шириною 2Δ, пари точок (x_i,y_i), (x_j,y_j), i,j = 1 ... 76 призначаються до інтервалу [r_o -Δ, r₀ + Δ] шляхом тестування r₀ –Δ ≤ d_ij <r₀ + Δ. Якщо використовується ваговий метод з ядром функції (3-99), ми повинні узагальнити знаки пар точок, що належать до кожного інтервалу і розділити кінцеву суму на кількість таких пар. З (3-97) і (3-100’) оцінка k_f (r) є завершена. Графік 3.35 показує, емпіричний знак кореляційної функції для наведених даних. Видно, що існує

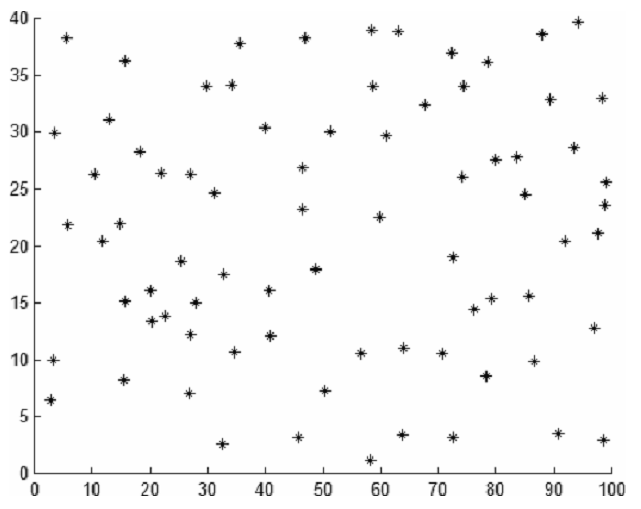
Графік. 3.34 Точковий шаблон, для прикладу 3.3.2.1 у вікні спостереження 100 × 40 квадратних метрів

локальний мінімум близько R = 4 м. Можливо, є "негативна взаємодія" поміж сусідніми деревами на малих відстанях. Цей факт може привести до менших величин DBH таких дерев. Тим не менше, немає значущого зв’язку для відстаней між деревами більше, ніж 8 метрів. Статистичний аналіз цих даних проведений нижче.

Іноді цікаво знати тип точкового процесу, до якого належить дана точкова діаграма. Ми почнемо з обговорення так званих точкових полів Пуассона.

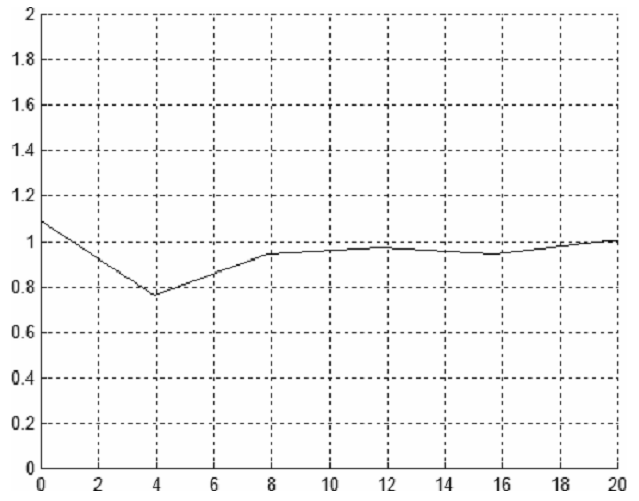
Графік. 3.35 Емпірична знакова кореляційна функція для прикладу 3.3.2.1. Відстані між точками r надані в метрах.

Пуасcонові точкові поля або коротше Пуасcонові поля є найпростішими і найбільш часто використовуваними формами точкових полів, тому що деякі корисні характеристики для них можна точно розрахувати. Термін "Пуассон" позначає розподіл кількості точкових чисел. Зокрема, число точок в непересічних (непересічні) наборах стохастично незалежне. Пуассонові поля використовуються для побудови більш складних моделей, таких як групові поля Неймана - Скотта. У цьому випадку точки діляться на два класи, відомі, як батьківські і дочірні точки. Перші прийшли початковий процес Пуассона, на другому етапі дочірні точки розкидані навколо кожної батьківської точки як насіння навколо «старого» дерева.