3.2.2.1 Змінна середньої

Метод зміни середньої, який заснований на локально адаптованій конструкції арифметичного способу , використовується для згладжування і фільтрації часових рядів.

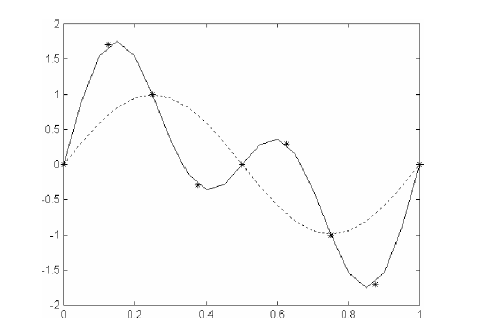
Рис. 3.22 Розрахункова тенденція до квазі-лінійних моделей (* 0,1, пунктирна лінія) і (* 0,5, суцільна лінія) для набору даних (зірок) з прикладу 3.2.2.1

Почнемо з часових рядів без так званого сезонного компонента , Це означає, що періодична функція або сезонна складова s (t) звертається в нуль в узагальненому поданні (3-71) :

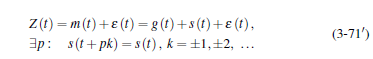
Математична модель часового ряду без сезонної складової дорівнює

Тепер ми сформулюємо загальне правило зміни середньої (2m + 1) для часових рядів без сезонної складової:

Нехай (t1, Z (t 1))….. (tN, Z (tN)) вимірювання приналежгості, до тимчасових рядів.

Для даного параметра m: m <(N -1) / 2. ми назвемо новий часовий ряд

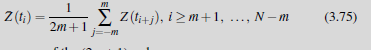
змінна середньої (2m+ 1) порядку.

Доведемо, як правило (3.75) працює, використовуючи набір даних із прикладу 3.2.2.1 для m= 1 і m= 2.

Приклад 3.2.2.2 Ми отримаємо згладжений часовий ряд застосування методу змінної середньої (3,75):

¯

• m = 1: зміннa середньої третього порядку. Правило (3,75)відноситься в цьому випадку до

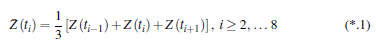
Наприклад, ми отримуємо

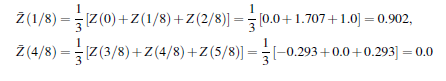
Згладжений часовий ряд задається

як показано на рис. 3.23a.

• m = 2: змінна середня п'ятого порядку. Правило (3,75) призводить до

Наприклад, має місце.

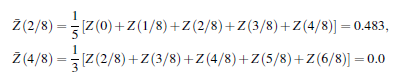
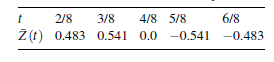
Згладжені часові ряди коротше і менш грубi, ніж оригінальні.

Згладження часових рядів відповідає

і показано на рис. 3.23b, де можна бачити, що згладжування часового ряду, застосовуючи так звану експонентне чи геометричне згладжування відіграє важливу роль, особливо для прогнозування майбутніх значень часового ряду. Цей метод заснований на зважених середніх арифметичних.

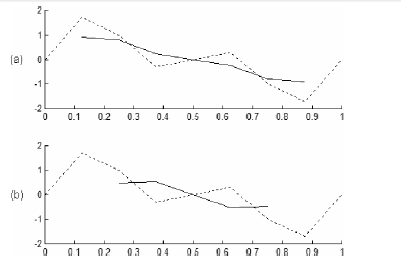
рис. 3.23 Згладжений часовий ряд (суцільна лінія) по змінній середньої третього порядку (a) і п'ятого порядку (b). Оригінал часові ряди тягнуться у вигляді пунктирних ліній.

3.2.2.2 Геометричне згладжування часових рядів.

Почнемо з загального правила:

Нехай Z (t) описують часовий ряд. Для даного параметра α: 0 <α <1 ми називаємо новий часовий ряд, створений

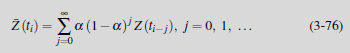
геометричне згладжування зі згладжуванням параметра α.. Бажано, щоб вибрати α: 0,2 <α <0,3. На підставі вимірів (t1, Z (t 1)) ,. , , , (tN, Z (tN)) передбачення на один крок може бути отримано

Наступний приклад являє собою застосування геометричного згладжування, забезпечуючи згладжування і один крок прогнозу.

Приклад 3.2.2.3 Вихідні дані залишаються незмінними:

Ми вибираємо параметр згладжування α = 0,25 Рекурсивний використовуючи (3-76) призводить до

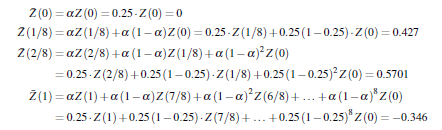
Малюнок 3.24 показує, що це геометричне вирівнювання . Прогноз на один крок в точці t = 1 + 1/8 = 1,125 можна досягти за допомогою (3-76’):

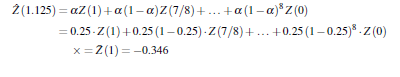
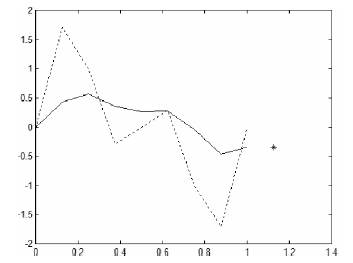
Рис. 3.24.Геометрична згладжування часових рядів (суцільна лінія) і один крок прогнозу в точці t = 1,125 (відзначений як зірки). Вихідні вимірювань наведені пунктирною лінією