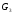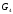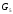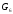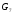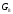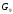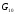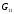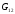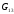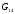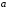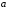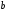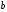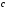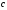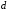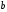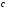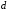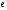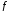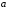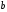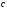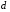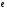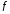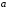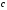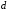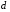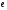- •Вступ до теорії графів методичні вказівки
- •6. 050103 „Програмна інженерія”
- •Теоретичні відомості Вступ
- •Основні означення теорії графів
- •Спеціальні види простих графів
- •Представлення графів
- •Ізоморфізм графів
- •Планарні та плоскі графи
- •Завдання до виконання
- •Контрольні запитання.
- •Список літератури
- •Вступ до теорії графів методичні вказівки
Завдання до виконання
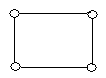
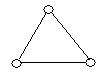
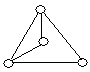
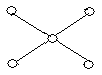
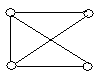
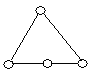
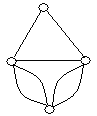
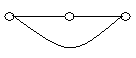
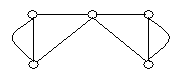
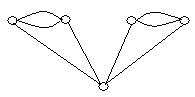
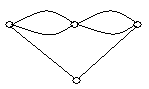
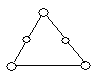
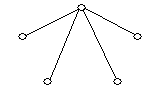
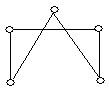
На рисунку зображено графи.
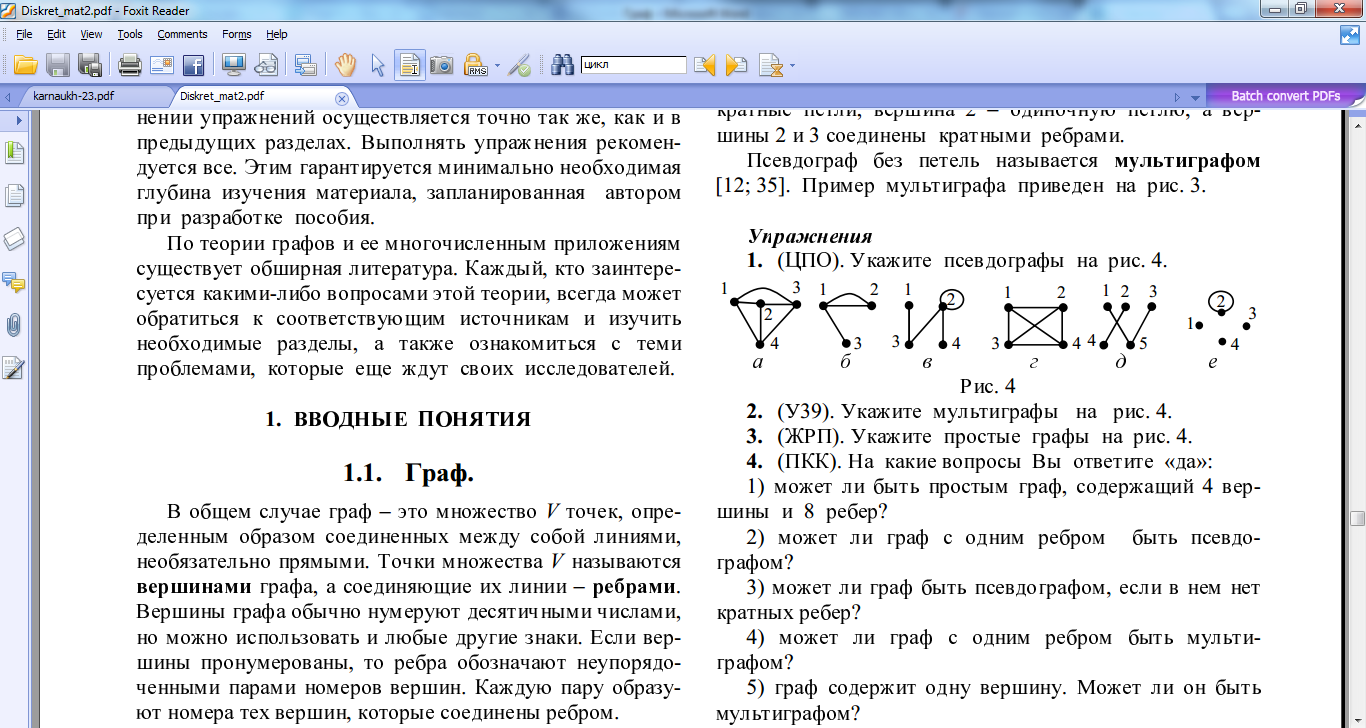
укажіть прості графи;
укажіть псевдографи;
укажіть мультиграфи;
укажіть кількість вершин та ребер (петель, кратних ребер) кожного графу;
укажіть степені кожної вершини графів.
Чи може бути граф простим, якщо він містить 4 вершини та 8 ребер?
Чи існує простий граф з степенями вершин, заданими нижче. Якщо не існує, то обґрунтуйте чому. Якщо існує, то зобразіть його.
а) 2,4,4,2,4; b) 1,1,1,1,1;
с) 1,1,1,1,2; d) 5,5,5,5,5;
e) 4,5,5,5,5; f) 2,2,4,4,4;
g) 1,1,2,2,4 h) 4,4,4,4,4.
Чи існує орієнтований простий граф із півстепенями вершин, заданими нижче. Якщо не існує, то обґрунтуйте чому. Якщо існує, то зобразіть його.
а) півстепені входу: 2,1,3,1,2; півстепені входу: 1,1,3,3,2;
b) півстепені входу: 2,1,1,1,2; півстепені входу: 1,1,3,1,2;
с) півстепені входу: 1,1,1,1,1; півстепені входу: 1,1,1,1,1;
d) півстепені входу: 1,1,0,1,0; півстепені входу: 2,1,0,0,0.
Чи може граф з однією вершиною бути мультиграфом?
Чи може граф з одним ребром бути мультиграфом? Псевдографом?
Обчисліть для кожного графу число півстепенів входу та виходу для кожної вершини.
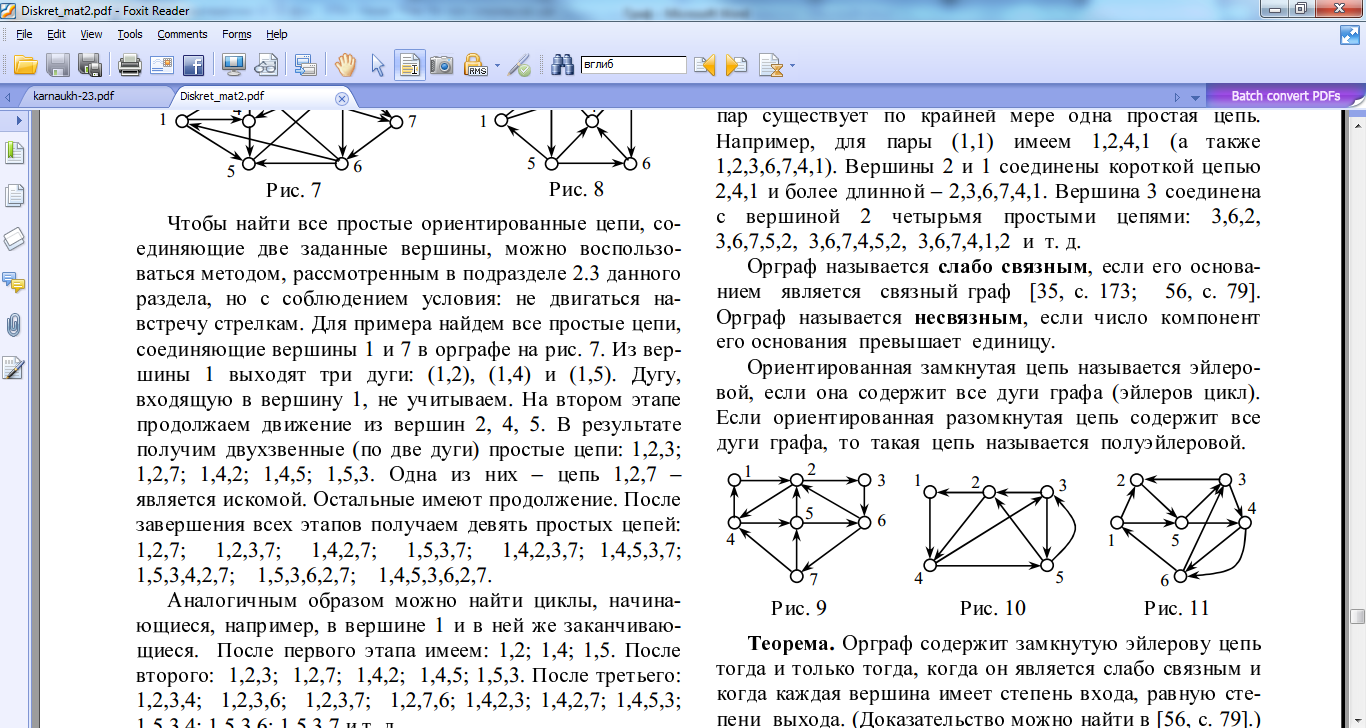
Побудувати графи:а) K5; б)K5,3; в)C7; г)W7; д)Q2.
Побудувати графи:а)
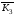 ;
б)
;
б)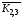 ;
в)
;
в)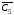 ;
г)
;
г)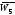 .
.
Графи G1, G2іG3представлені у вигляді:
G1= {V1, Е1}, деV1= {1, 2, 3, 4, 5, 6};Е1= {{1, 2}, {1, 3}, {1, 4},{2, 3}, {2, 6}, {3, 5}, {3, 6}, {5, 6}};
G2= {V2, Е2}, деV2= {1,2,3,4,5,6,7,8}; Е2= {{1,4}, {2,3}, {3,5}, {3,6}, {5,6}, {5,7},{5,8}, {6,7}, {6,8}};
G3= {V3, Е3}, деV3= {3,4,5,6,7,8,9};Е3= {{3,5}, {3, 6}, {3, 8}, {4, 6}, {5, 6}, {5, 7}, {6, 7}, {7, 8}, {7, 9}, {8, 9}}.
Обчислити кількість вершин та ребер в графах:
G=G1
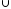 G2;
G2;G=G2
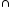 G3;
G3;G=G1
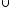 G2
G2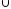 G3;
G3;G=G1
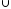 (G2
(G2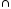 G3).
G3).
Обчислити кількість вершин та ребер у G=G1
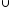 G2,G=G1
G2,G=G1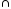 G2,
G2,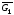 ,
,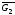 .
.
|
|
|
|
G1 |
G2 |
Скільки ребер в однорідному графі, якщо n= 7 и deg(v) = 6?
В однорідному графі степінь вершини дорівнює 5. Кількість ребер дорівнює 35. Знайдіть кількість вершин.
Чи існує однорідний граф із 6 вершинами та 9 ребрами?
У повному графі 18 вершин. Скільки в ньому ребер, інцидентних одній вершині?
Скільки ребер в повному графі із 10 вершинами?
Повний граф містить 105 ребер. Скільки в ньому вершин?
Чи існує повний граф, кількість ребер якого дорівнює 15?
Який степінь вершини повного графу, який містить 91 ребро.
Який вигляд має доповнення графа Kn,m?
Який з графів є дводольним? Які з цих графів є однорідними?
У графі G5 вершин та 4 ребра. Скільки ребер та вершин у графі
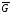 ?
?
У графі Сn8 ребер. Скільки ребер та вершин у графі
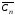 ?
?
У графі Wn30 ребер. Скільки ребер та вершин у графі
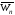 ?
?
Задано W16. Скільки ребер та вершин у графі
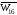 ?
?
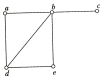
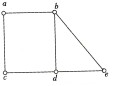
Задати матрицями інцидентності, суміжності, списком ребер, списком суміжності неорієнтовані графи, зображені на рисунку:
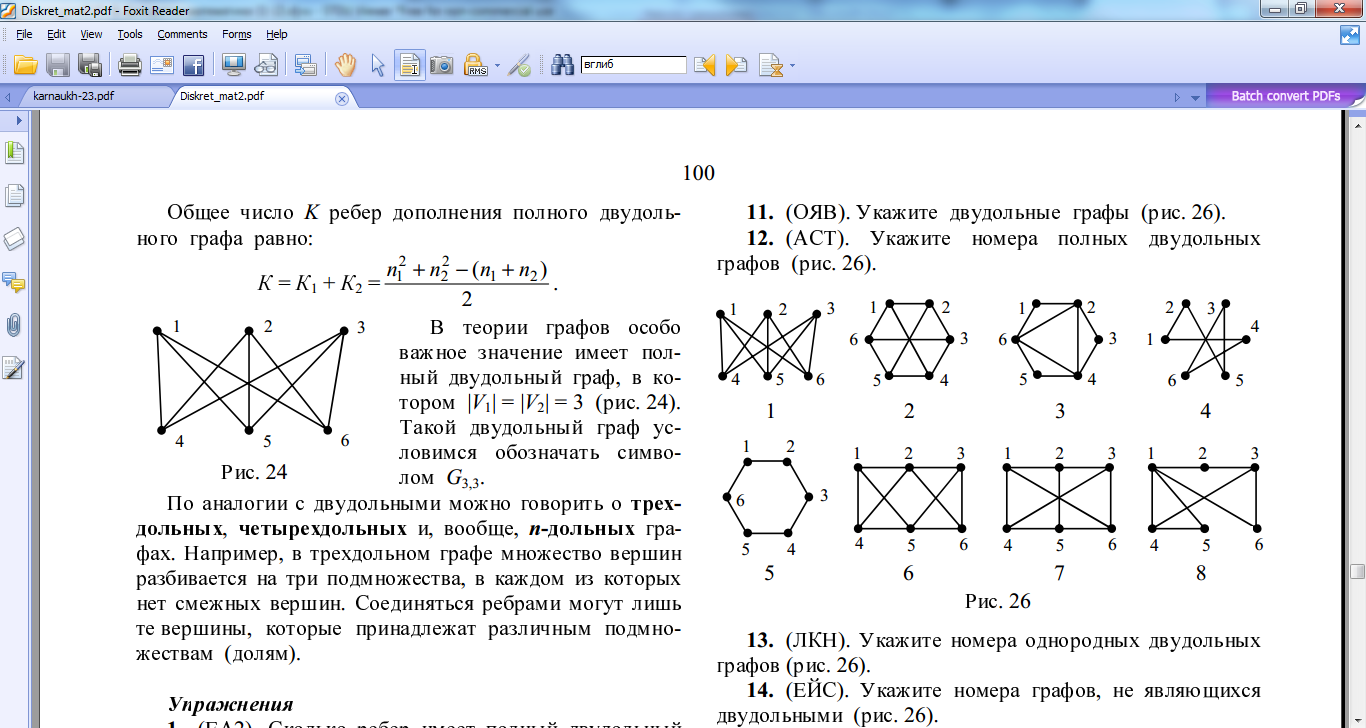
Задати матрицями інцидентності, суміжності, списком ребер, списком суміжності орієнтовані графи, зображені на рисунку:
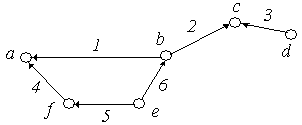
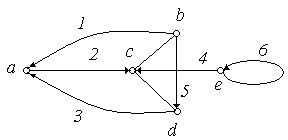
Запишіть матриці інцидентності для графів із вправи 1.
Запишіть матриці суміжності для графів із вправи 1.
Запишіть списки пар для графів із вправи 1.
Запишіть списки суміжності для графів із вправи 1.
Запишіть матриці інцидентності для графів із вправи 7.
Запишіть матриці суміжності для графів із вправи 7.
Запишіть списки пар для графів із вправи 7.
Запишіть списки суміжності для графів із вправи 7.
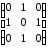
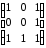
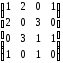
Зобразити неорієнтовані графи за матрицями суміжності:
|
|
|
|
Для заданих матриць інцидентності а) іб) знайти відповідний граф та записати матриці суміжності.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 | |
|
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 | |
|
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 | |
|
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 | |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
а)б)
Для заданих матриць суміжності а) іб) знайти відповідний граф.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 | |||
|
|
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 | |||
|
|
1 |
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 | |||
|
|
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 | |||
|
|
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 | |||
|
|
0 |
1 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
0 |
а) б)
Записати матриці суміжності та списки суміжності для графів.
|
|
|
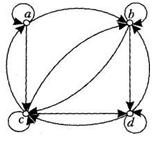
Визначити, які пари орієнтованих графів ізоморфні.
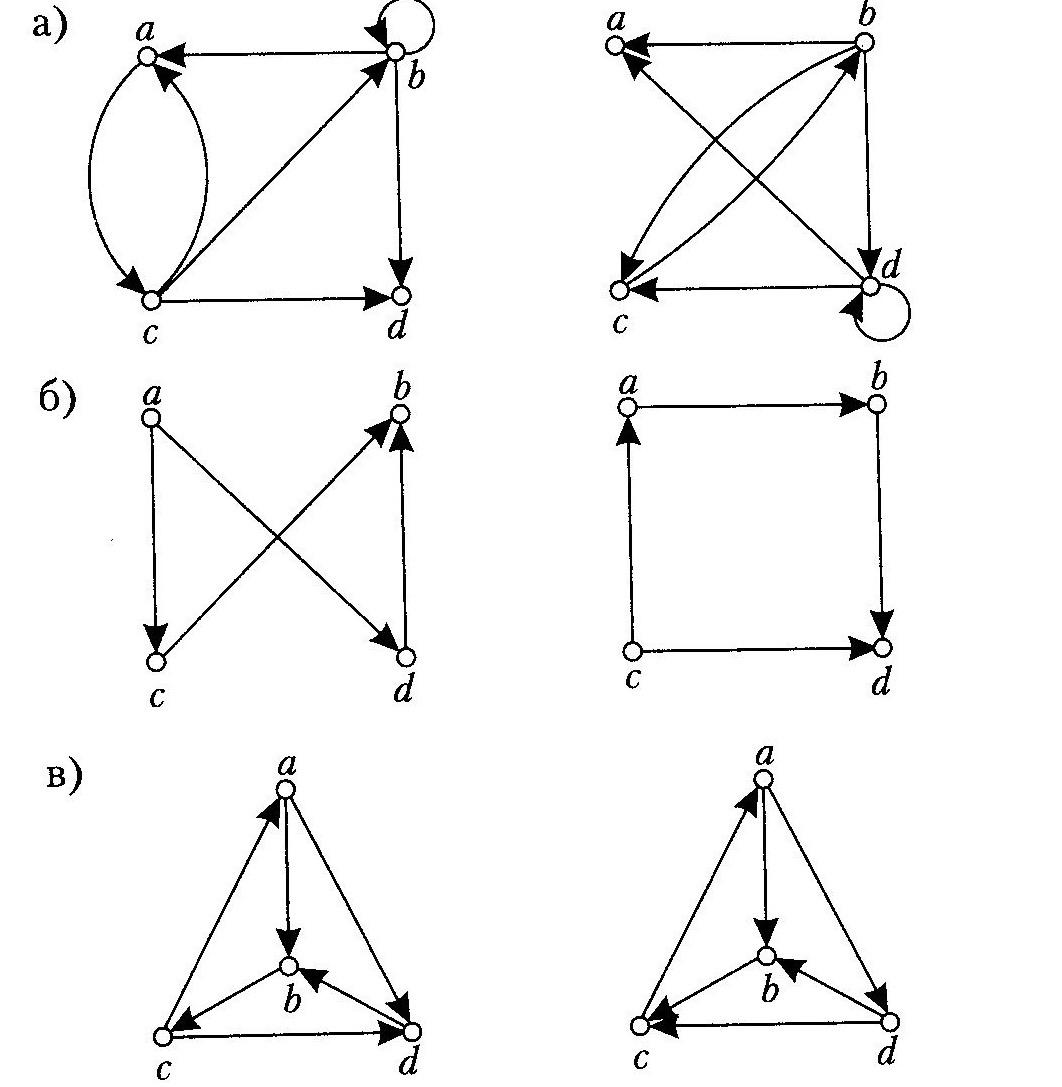
Які пари графів, представлених на рисунку ізоморфні?