3. Представлення графів

Найзрозумілішим і найпростішим для людини є графічний спосіб подання графу, коли граф зображають на рисунку у вигляді сукупності точок, з’єднаних між собою лініями. Але цей спосіб не придатний для опрацювання графів на комп’ютері.

Розглянемо деякі способи подання для неорієнтованого та орієнтованого графів.

Матриця інцидентності.

Матриця інцидентності – матриця, у якій для кожного ребра вказані інцидентні йому вершини. Рядкам матриці відповідають номера вершин, стовпцям – ребра графа.

Для неорієнтованого графу формула знаходження елементів матриці інцидентності має вигляд:

.

Зауважимо, що для простого графа в матриці інцидентності в кожному стовпці точно дві одиниці, і немає однакових стовпців. Матрицю інцидентності можна викори­стовувати й для подання мультиграфа. У такому випадку можуть з'являться однакові стовпці (вони відповідають кратним ребрам). Для поданняпсевдографа, якщо в ньому є петлі, у відповідних позиціях матриці ставимо 2 (у цьому разі матриця інцидентності не булева).

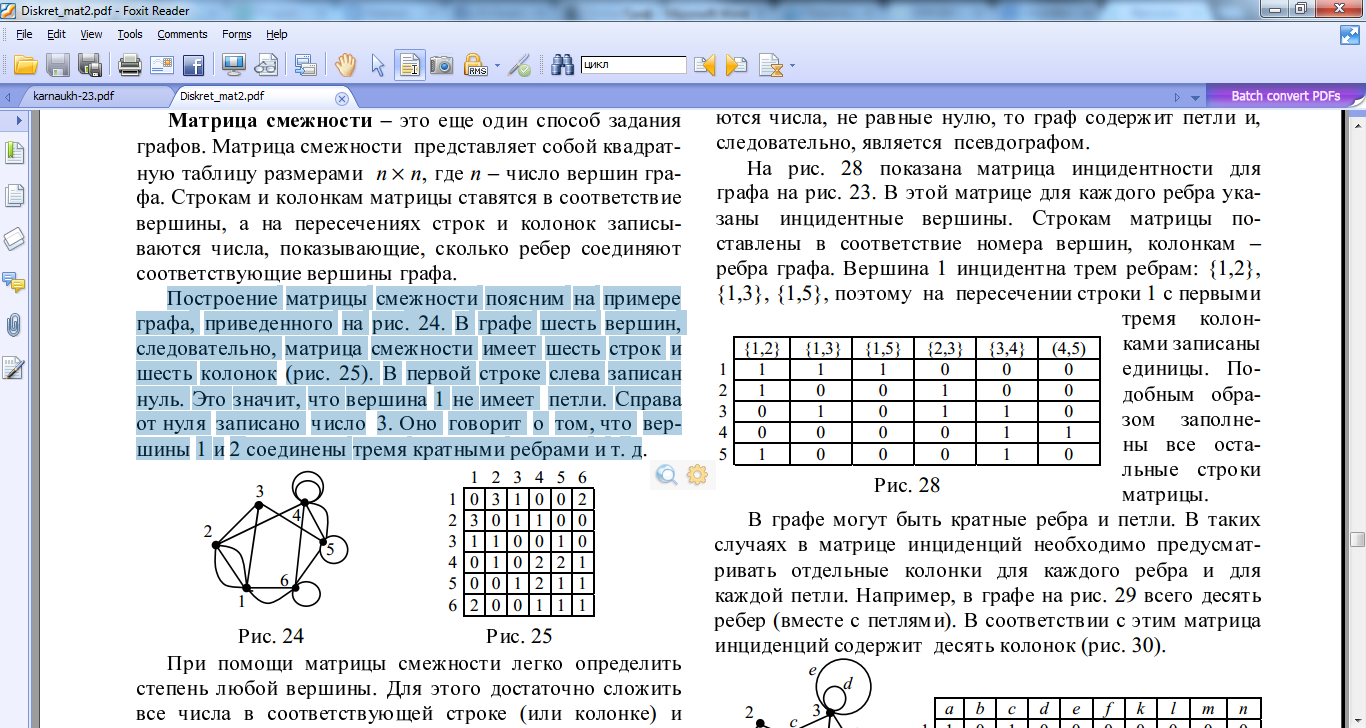
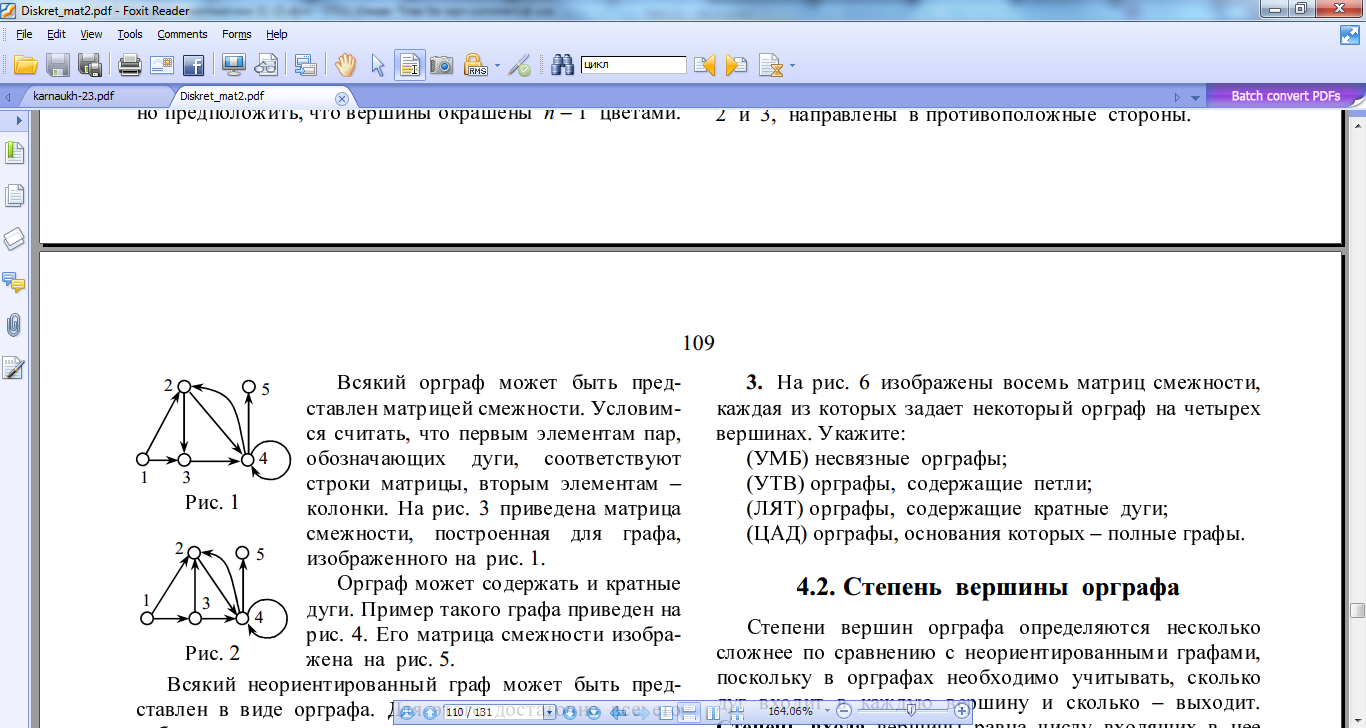
Побудову матриці інцидентності легко пояснити на прикладі графа, наведеного на рис. 3.1. У графі п’ять вершин, отже, матриця інцидентності має п’ять рядків, також у графі 10 ребер (для зручності кожне з них позначене малою латинською літерою), тому матриця інцидентності має 10 стовпців (табл.3.1). У першому стовпці елементи а₁₁=1 таа₂₁=1, а це означає, що ребро «а» з’єднує вершину «1» та «2». Елемента₃₄=2 означає те, що вершина «3» має петлю і т. д.

	a b c d e f k l m n 1 1 0 1 0 0 0 0 0 0 0 2 1 1 0 0 0 0 0 0 0 0 3 0 0 1 2 2 1 1 0 0 0 4 0 1 0 0 0 0 1 1 1 0 5 0 0 0 0 0 1 0 1 1 2
Рис. 3.1. Приклад неорієнтованого графа	Матриця інцидентності графа, зображеного на рис.3.1.

За допомогою матриці інцидентності можна подавати й орієнтовані графи. Для орієнтованого графу формула знаходження елементів матриці інцидентності має вигляд:

.

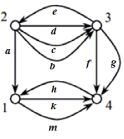
Розглянемо матрицю інцидентності для орграфа (рис.3.2). Для зручності кожну дугу графу позначено малою латинською літерою. Перший стовпець показує напрям дуги «а». Елементи а₁₁=-1,а₂₁=1 означає, що дуга «а» виходить з першої вершини та входить в другу і т.д.

	a	b	c	d	e	f	g	h	k	m
1	-1	0	0	0	0	0	0	-1	1	1
2	1	1	1	1	-1	0	0	0	0	0
3	0	-1	-1	-1	1	1	1	0	0	0
4	0	0	0	0	0	-1	-1	1	-1	-1

Рис. 3.2. Приклад орієнтованого графа

Матриця інцидентності графа, зображеного на рис.3.2.

З алгоритмічного погляду представлення графу на комп’ютері матриця інцидентності, мабуть, найгірший спосіб подання, адже для неї потрібно n×mкомірок пам'яті, більшість із яких зайняті нулями. По-друге, доступ до інформації незручний. Щоб отримати відповідь на елементарні питання (наприклад, чи існує дуга (v_i, v_j)), у найгіршому випадку потрібно перебрати всі стовпці матриці, тобто виконатиmкроків.

Матриця суміжності.

Матриця суміжності – це квадратна таблиця розміром n×n, деn – число вершин графа. Рядкам і стовпцям матриці ставляться у відповідність вершини, а на перетинах рядків і колонок записуються числа, які показують, скільки ребер з'єднують відповідні вершини графа.

Для неорієнтованого графу формула знаходження елементів матриці суміжності має вигляд:

,

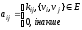де v_i, v_j – вершини графа,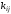– кількість ребер, що виходять з вершиниv_iта входять у вершину v_j.

Зауважимо, що матриця суміжності неорієнтованого простого графу є симетричною відносно головної діагоналі і булевою. Головна діагональ відповідає за наявність петель. Якщо будувати матрицю суміжності для мультиграфа, тоді матриця буде не булевою. Елемент a_ijбуде дорівнювати кратності ребер, що з’єднують відповідні вершиниv_iта v_j.

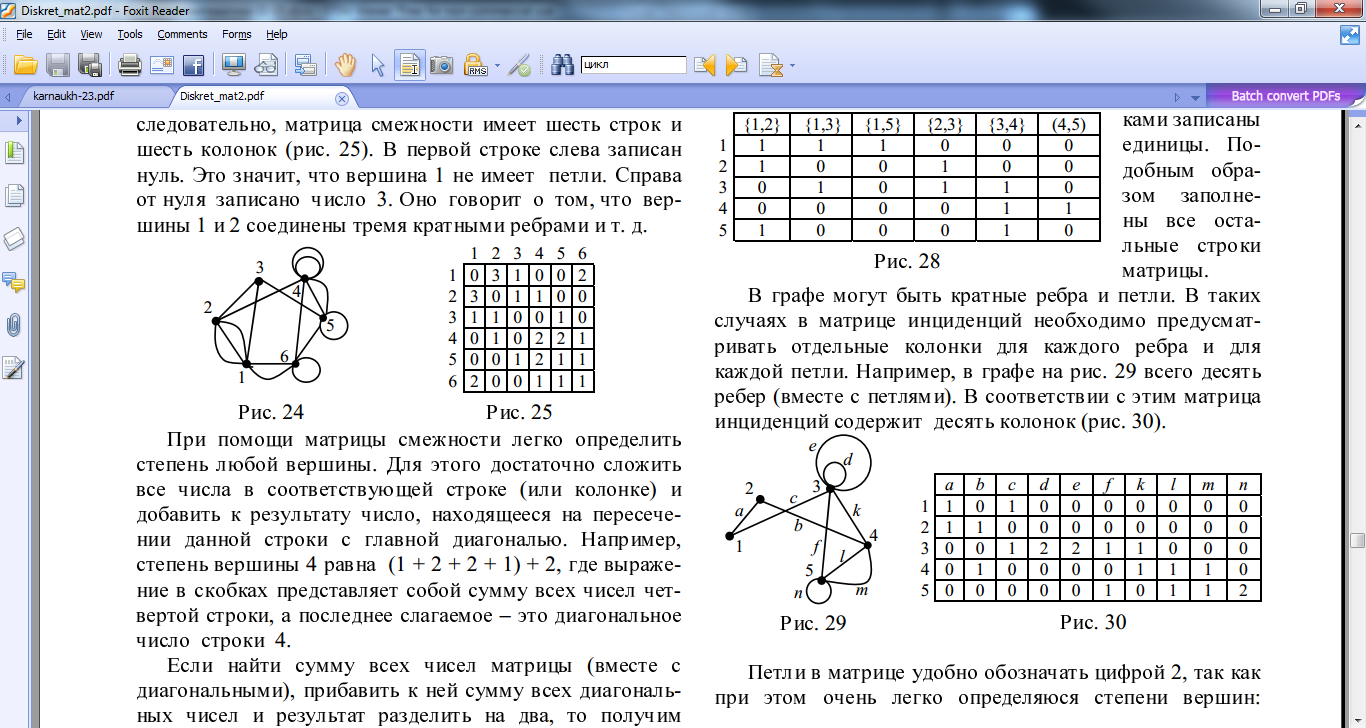
Побудову матриці суміжності легко пояснити на прикладі графа, наведеного на рис. 3.3. У графі шість вершин, отже, матриця суміжності має шість рядків і шість стовпців (рис.3.3). Елемент а₁₁=0 означає, що вершина «1» не має петлі. Елемента₁₂=3 означає те, що вершини «1» і «2» з'єднані трьома кратними ребрами і т. д.

	1 2 3 4 5 6 1 0 3 1 0 0 2 2 3 0 1 1 0 0 3 1 1 0 0 1 0 4 0 1 0 2 2 1 5 0 0 1 2 1 1 6 2 0 0 1 1 1
Рис. 3.3. Приклад неорієнтованого графа	Матриця суміжності графа, зображеного на рис.3.3.

За допомогою матриці суміжності легко можна обчислити степінь будь-якої вершини. Для цього достатньо додати всі числа відповідного рядка (або стовпчика) і додати до результату число, що знаходиться на перетині даного рядка з головною діагоналлю. Наприклад, степінь вершини «4» дорівнює (1+2+2+1)+2.

Для орієнтованого графу формула знаходження елементів матриці суміжності має вигляд:

,

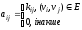де v_i, v_j – вершини графа,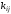– кількість дуг, що виходять з вершиниv_iта входять у вершину v_j..

Для простого орієнтованого графу матриця суміжності зазвичай не симетрична та булева. Якщо розглядати орієнтований мультиграф, то елемент a_ij дорівнює кількості дуг, які мають v_i початковою вершиною, а v_j – кінцевою.

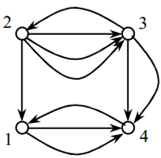
Розглянемо матрицю суміжності для орграфа (рис.3.4). Діагональні елементи матриці суміжності дорівнюють нулю через відсутність петель. Елемент а₁₂=0, адже з вершини «1» у вершину «2» не виходить жодної дуги. Елемента₁₄=2, адже з вершини «1» у вершину «4» виходить дві дуги і т.д.

	1 2 3 4 1 0 0 0 2 2 1 0 3 0 3 0 1 0 2 4 1 0 0 0
Рис. 3.4. Приклад орієнтованого графа	Матриця суміжності графа, зображеного на рис.3.4.

Велика перевага матриці суміжності як способу подання графа – швидкий дос­туп до інформації: за один крок можна одержати відповідь на питання, чи існує ребро (дуга) з v_iу v_j. Окрім того перевагою матриці суміжності є легка перевірка на тип графу – простий, мульти- чи псевдограф. Якщо в матриці окрім одиниць та нулів є інші числа – це мультиграф, якщо на діагоналі не всі елементи рівні нулю – це псевдограф. Недолік такого способу подання полягає в тому, що незалежно від кількості ребер обсяг пам'яті становитьn²комірок.

Список пар (список ребер).

Ще одним способом представлення графу є список пар, що відповідають ребрам (або дугам) такого графу. Пара [v_i, v_j ] відповідає ребру {v_i, v_j} у випадку неорієнтованого графу і дузі (v_i, v_j) – у випадку орієнтованого.

Розглянемо представлення неорієнтованого графу на прикладі (рис. 3.5). У список записуються в лексикографічному порядку усі існуючі ребра. Кількість пар дорівнює кількості ребер графу.

	v1 v1 v1 v2 v1 v3 v2 v2 v2 v4 v3 v4 v3 v4 v3 v4
Рис. 3.5. Приклад неорієнтованого графа	Список пар для графу, зображеного на рис.3.5

На рис. 3.6 наведено представлення списком пар орієнтованого графу. У список записується в лексикографічному порядку усі існуючі дуги. Кількість пар дорівнює кількості дуг орграфу.

	v1 v2 v1 v3 v2 v3 v2 v4 v3 v4 v4 v2 v4 v4 v4 v5
Рис. 3.6. Приклад орієнтованого графа	Список пар для графу, зображеного на рис.3.6

Метод зображення графа списком пар, які відповідають його ребрам (або ду­гам), значно економніший щодо пам'яті, особливо якщо m(кількість ребер) значно менша, ніжn²(n– кількість вершин). Очевидно, що обсяг пам'яті в цьому разі дорівнює 2m. Недоліком такого способу подання графу є велика кількість кроків для знаходження множини вершин, до яких ідуть ребра чи ду­ги із заданої вершини. Ситуацію можна значно покращити, упорядкувавши множину пар лексикографічно та застосувавши двійковий пошук.

Список суміжності.

Такий спосіб подання графу використовують тоді, коли кількість ребер значно менша, ніж кількість вершин в квадраті (m<<n²), а також для випадків динамічних графів, коли у графі постійно додаються нові вершини та ребра.

Зазвичай такий спосіб подання використовується для орграфів. Для використання списку суміжності неорієнтованого графа можна попередньо замінити кожне ребро на дві протилежно напрямлені дуги.

Розглянемо представлення орієнтованого графу на прикладі (рис. 3.7). Список суміжності містить два стовпці: у перший записується вершина, у другий – множина вершин, у які існує дуга з першої. Кількість рядків дорівнює кількості вершин графу.

Вершина виходу	Вершина входу
v1	v2, v3
v2	v3, v4
v3	v4
v4	v2, v4, v5
v5

Рис. 3.7. Приклад орієнтованого графа

Список суміжності для графу, зображеного на рис.3.7

На рис. 3.8 наведено представлення списком суміжності неорієнтованого графу. Попередньо кожне ребро графу замінили двома протилежно напрямленими дугами.

Вершина виходу		Вершина входу
v1	v1, v2, v3
v2	v1, v2, v4
v3	v1, v4, v4, v4
v4	v2, v3, v3, v3

Рис. 3.8. Приклад неорієнтованого графа

Список суміжності для графу, зображеного на рис.3.8

Головний недолік такого способу подання графу є неможливість швидко перевірки наявності дуги (v_i, v_j).