
Розділ 2.
2. Електростатика

Електростатика вивчає властивості і взаємодію нерухомих у певній системі координат електричних зарядів.
Електричним зарядом називається скалярна фізична величина, яка визначає здатність заряджених частинок вступати в електромагнітну взаємодію між собою. У природі існує два види електричних зарядів: додатні і від’ємні.
У процесі електризації тертям одне тіло набуває додатного заряду, а друге від’ємного. Величина додатного заряду одного тіла точно дорівнює величині від’ємного заряду другого тіла. Це положення відоме від назвою закону збереження електричного заряду: електричні заряди не виникають і не зникають, вони можуть лише передаватися від одного тіла до іншого або переміщатися всередині даного тіла. Тому алгебраїчна сума зарядів, які виникають на всіх тілах, що беруть участь у цьому процесі, завжди дорівнює нулю. Експериментально доведено, що всі так звані “елементарні” заряджені частинки (електрони, позитрони, протони) мають заряд 1,60210-19 Кл.
2.1 Взаємодія електричних зарядів. Закон Кулона.
Кулон
експериментально встановив закон
взаємодії електричних зарядів. Закон
Кулона справджується для точкових
зарядів. Під точковим зарядом розуміють
заряджене тіло, розміри якого досить
малі порівняно з іншими зарядами.
Вивчаючи взаємодію заряджених тіл за
допомогою
![]() крутильних
терезів, Кулон встановив:величина
сили взаємодії двох точкових зарядів
прямо пропорційна добутку величин цих
зарядів і обернено пропорційна квадратові
відстані між ними, тобто:
крутильних
терезів, Кулон встановив:величина
сили взаємодії двох точкових зарядів
прямо пропорційна добутку величин цих
зарядів і обернено пропорційна квадратові
відстані між ними, тобто:
![]()
![]() (2.1)
(2.1)
де k– коефіцієнт пропорційності.
![]() -
діелектрична проникність середовища,
-
діелектрична проникність середовища,
![]() -
електрична стала..
-
електрична стала..
Кулонівські сили – центральні, тобто вони спрямовані вздовж прямої, яка сполучає точкові заряди. Однойменні заряди відштовхуються, а різнойменні притягуються ( рис. 2.1).
Рис. 2.1

З цього закону випливає, що за одиницю електричного заряду (Кулон - Кл) вважають такий точковий заряд, який діє у вакуумі на такий самий заряд, розміщений на відстані 1 м з силою 9109 Н.
2.2 Напруженість електричного поля.
Графічне зображення електричного поля.
Кожний електричний
заряд
завжди змінює властивості простору,
який його оточує, створюючи в ньому
електричне поле. Це поле проявляється
таким чином, що при вміщенні в ньому в
будь-якій точці електричного заряду на
нього буде діяти сила. Будь-яка точка
електричного поля характеризується
напруженістю
![]() і потенціалом.
і потенціалом.
Напруженість
![]() електричного поля є його силовою
характеристикою, оскількивона
чисельно дорівнює силі
електричного поля є його силовою
характеристикою, оскількивона
чисельно дорівнює силі
![]() ,
яка діє на одиничний додатній точковий
заряд, розміщений в даній точці поля.
Напрям вектора
,
яка діє на одиничний додатній точковий
заряд, розміщений в даній точці поля.
Напрям вектора
![]() в даній точці простору співпадає з
напрямком сили
в даній точці простору співпадає з
напрямком сили![]() ,
яка діє на додатній пробний заряд,
вміщений у цю точку (рис. 2.2а).
,
яка діє на додатній пробний заряд,
вміщений у цю точку (рис. 2.2а).
![]() ,
(2.2)
,
(2.2)
Якщо електричне поле створюється нерухомим точковим зарядом q, то напруженість поля в точці, яка віддалена від цього заряду на відстань r, згідно з (1) і (2) дорівнюватиме:
![]() (2.3)
(2.3)
Вектор
![]() завжди напрямлений вздовж радіальної
прямої, яка проходить через зарядq
і дану точку поля: якщо заряд q
додатній, то вектор
завжди напрямлений вздовж радіальної
прямої, яка проходить через зарядq
і дану точку поля: якщо заряд q
додатній, то вектор
![]() напрямлений від заряду, а коли зарядq
від’ємний
– до заряду, як показано на (рис. 2.2 (б))
і (рис. 2.2 (в)).
напрямлений від заряду, а коли зарядq
від’ємний
– до заряду, як показано на (рис. 2.2 (б))
і (рис. 2.2 (в)).
Рис.
2.2
![]()
![]() (2.4)
(2.4)
Останнє твердження називається принципом суперпозиції електричних полів, який дає можливість визначати напруженість електричного поля будь-якої системи зарядів.
Електричне
поле можна графічно зобразити за
допомогою ліній напруженості, які
називаються силовими лініями. Їх
проводять таким чином, щоб дотична до
них у кожній точці співпадала з напрямом
вектора
![]() .
Силові лінії електричного поля починаються
на додатному заряді і закінчуються на
від’ємному ( рис. 2.3 ) або радіально
розходяться в безмежність.
.
Силові лінії електричного поля починаються
на додатному заряді і закінчуються на
від’ємному ( рис. 2.3 ) або радіально
розходяться в безмежність.
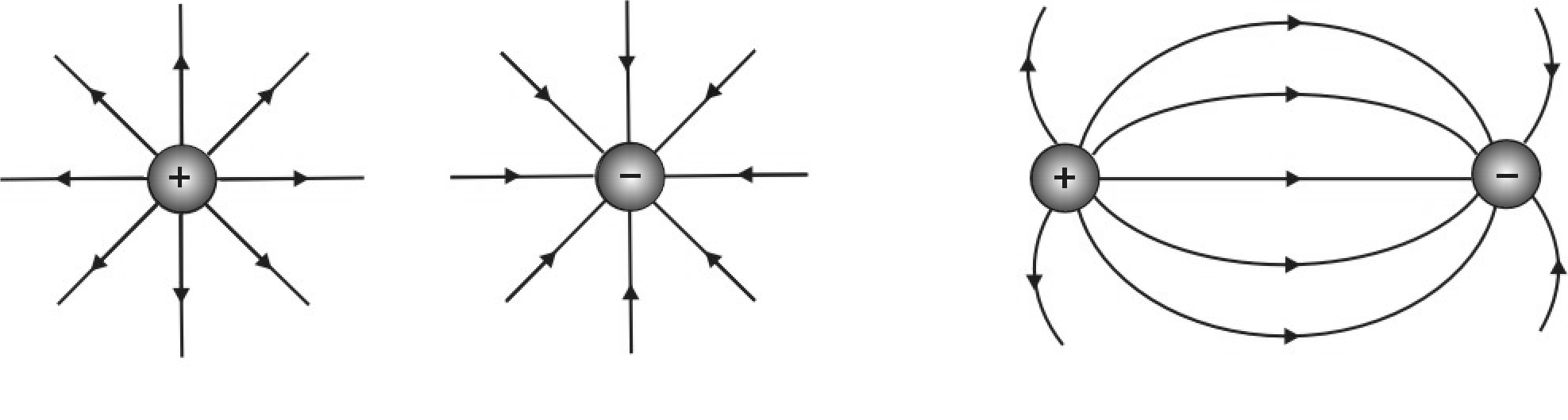
Рис. 2.3
Фізична величина, яка чисельно дорівнює потенціальній енергії, яку має одиничний додатний заряд, вміщений в певну точку електростатичного поля, називається потенціалом поля в цій точці. Потенціал є енергетичною характеристикою поля:
![]() (2.5)
(2.5)
В полі точкового заряду q потенціальна енергія пробного заряду q+np визначається наступним співвідношенням:
![]() (2.6)
(2.6)
Якщо поле створюється додатним зарядом, то його потенціальна енергія Wп>0, отже >0, а коли від’ємним - то Wп<0 і <0. Із виразів (2.5) і (2.6) для поля точкового заряду знаходимо:
![]() (2.7)
(2.7)
Потенціал електростатичного поля створеного системою зарядів, в довільній точці поля дорівнює алгебраїчній сумі потенціалів, створених кожним із зарядів в цій точці:
![]() (2.8)
(2.8)
Із виразу (2.5) випливає, що потенціальна енергія пробного додатного заряду:
![]() (2.9)
(2.9)
Коли пробний заряд перемістити з однієї точки поля в іншу, то матимемо роботу сил електричного поля, яка виконується при переміщенні цього заряду:
![]() (2.10)
(2.10)
Із виразу (2.7) видно, що потенціал точкового заряду є функцією відстані від заряду, який створює поле, до точки, в якій визначається потенціал. Геометричне місце точок однакового потенціалу називають еквіпотенціальною поверхнею. Лінії напруженості електричного поля завжди перпендикулярні до еквіпотенціальної поверхні (рис. 2.4).

Рис. 2.4
Напруженість
електричного поля
![]() і потенціал
зв’язані
і потенціал
зв’язані
співвідношенням:
![]() (2.11)
(2.11)
(знак
„-“ вказує на те, що напрям вектора
![]() збігається з напрямом зменшення
потенціалу).
збігається з напрямом зменшення
потенціалу).
Проекції
вектора
![]() на осі координат мають вигляд:
на осі координат мають вигляд:
![]()
![]()
![]() (2.12)
(2.12)
Результуючий
вектор
![]() дорівнює:
дорівнює:![]()
![]() (2.13)
(2.13)
де
![]() ,
,![]() ,
,![]() – одиничні вектори, напрямлені по осях
координат.
– одиничні вектори, напрямлені по осях
координат.
Елементарна
робота переміщення заряду в електричному
полі на відстань
![]() дорівнює:
дорівнює:
![]() (2.14)
(2.14)
Тоді робота переміщення пробного заряду з точки 1 в точку 2 (рис. 2.5), в яких потенціали будуть відповідно 1 і 2, визначаються співвідношенням:
![]() (2.15)
(2.15)
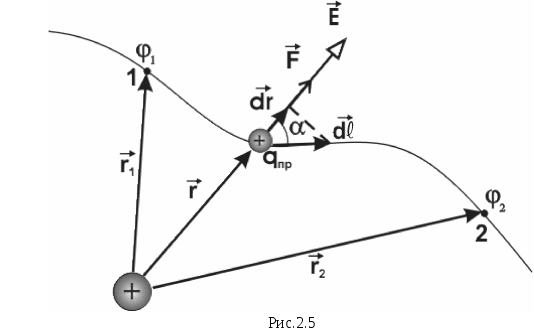
З рівняння (2.15) випливає:
![]() (2.16)
(2.16)
Якщо пробний заряд переміщується в електричному полі по замкнутій траєкторії і повертається у вихідну точку, то 1 = 2, і рівняння (2.16) можна переписати:
![]()
![]() (2.17)
(2.17)
Співвідношення
(2.17)
справедливе тільки для електростатичного
поля, а вираз
![]() називається
циркуляцією вектора напруженості вздовж
замкнутого контуру.
Отже, в електричному полі циркуляція
вектора напруженості вздовж замкнутого
контуру дорівнює нулю.
називається
циркуляцією вектора напруженості вздовж
замкнутого контуру.
Отже, в електричному полі циркуляція
вектора напруженості вздовж замкнутого
контуру дорівнює нулю.
