
- •Технічний коледж
- •Методичні вказівки до виконання практичних робіт
- •Тема 1:Складання математичної моделі об’єкта керування
- •Тема 2: Типові ланки систем автоматичного керування
- •Тема 3: Способи з’єднання ланок та їх еквівалентні передаточні функції.
- •Послідовне з’єднання ланок
- •Паралельне з’єднання ланок
- •Тема 4: Амплітудні та фазові частотні характеристики елементарних ланок
- •Тема 5: Визначення стійкості. Алгебраїчні критерії стійкості. Критерії стійкості Гурвіца і Рауса.
- •Тема 6: Лінійна та квадратична інтегральні оцінки якості
- •Тема 8: Метод гармонічної лінеаризації (гармонічного балансу). Гармонічний коефіцієнт передачі нелінійного елемента.
- •Тема 9: Дискретні системи автоматичного керування
- •Завдання для самоконтролю:
Тема 9: Дискретні системи автоматичного керування
Теоретичні відомості
В режимі амплітудно-імпульсної модуляції імпульсний елемент виробляє прямокутні імпульси однакої сквапності з амплітудою імпульсів пропорційною до величини вхідного сигналу в моменти квантування. На час дії імпульсу амплітуда залишається сталою.
Структурна
схема імпульсного елемента складається
з послідовного з’єднання ідеальної
імпульсної ланки і формуючої ланки.
Ідеальна імпульсна ланка здійснює
вибірку вхідного сигналу. Вона є чисто
імпульсним елементом, котрий генерує
послідовність
 - дельта імпульсів з площею пропорційною
до величини вхідного сигналу в моменти
квантування
- дельта імпульсів з площею пропорційною
до величини вхідного сигналу в моменти
квантування

Формуюча
ланка з кожного
 - імпульсу формує прямокутні імпульси
з амплітудою пропорційною до величини
площі імпульсів. Реакцію формуючої
ланки на
- імпульсу формує прямокутні імпульси
з амплітудою пропорційною до величини
площі імпульсів. Реакцію формуючої
ланки на - імпульс називають імпульсною перехідною
характеристикою, або ваговою функцієюw.
Прямокутний імпульс можна сформувати
з двох ступінчатих функцій зсунутих по
часу на величину тривалості імпульсу
- імпульс називають імпульсною перехідною
характеристикою, або ваговою функцієюw.
Прямокутний імпульс можна сформувати
з двох ступінчатих функцій зсунутих по
часу на величину тривалості імпульсу
 .
В результаті вираз для імпульсної
перехідної характеристики приймає
вигляд
.
В результаті вираз для імпульсної
перехідної характеристики приймає
вигляд

Зображення Лапласа від імпульсної перехідної характеристики є передаточною функцією формуючої ланки. Таким чином формуюча ланка є аналоговою, а вираз для передаточної функції знаходять на основі зображення Лапласа

Задача №1. Знайти передаточну функцію розімкнутої імпульсної системи. Система складається з імпульсного елемента і неперервної частини.
Імпульсний елемент здійснює амплітудно-імпульсну модуляцію, тобто виробляє прямокутні імпульси з відносною тривалістю y – 0,1. Період слідування імпульсу 0,1с. Неперервна частина – інерційна ланка 1-го порядку: к=1 і Т=1с.
 U
y
U
y












Намалюємо 2 структурну схему, в якій імпульсний елемент представлений двома ланками. Формуюча ланка є аналоговою ланкою.

 U
y
U
y










 При
При


Знайдемо передаточну функцію зведеної неперервної частини:

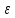
 y
y







Передаточна
функція розімкнутої системи
 .
На вході діє сигнал
.
На вході діє сигнал ,
на виході
,
на виході .
Беремо дискретне зображення Лапласа
від решітчастої функції:
.
Беремо дискретне зображення Лапласа
від решітчастої функції: .
Оскільки
.
Оскільки ,
тоді
,
тоді

 –дискретна
передаточна функція. Тоді
–дискретна
передаточна функція. Тоді
 .
.
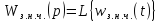 ,
по аналогії можна записати:
,
по аналогії можна записати:

 .
Використовуючи таблицю Z-зображень,
передаточна функція розімкнутої
імпульсної системи буде:
.
Використовуючи таблицю Z-зображень,
передаточна функція розімкнутої
імпульсної системи буде:


Завдання для самоконтролю:
Задача №1
Знайти передаточну функцію з’єднання:
2















Задача №2
Знайдіть зображення за Лапласом для одиничної ступінчатої функції.
Задача №3
Знайти
еквівалентну передаточну функцію
послідовного з’єднання двох ланок,
якщо їх передаточні функції відповідно
 ;
;
 .
.
Задача №4
Записати
передаточну функцію ланки, якщо операторна
форма диференційного рівняння має
вигляд:
 .
.
Задача №5
Знайти
розв’язок диференційного рівняння
 якщо
якщо
 і початкові умови нульові.
і початкові умови нульові.
Задача №6
Знайти
еквівалентну передаточну функцію
паралельного зустрічного з’єднання
двох ланок, якщо ланка з передаточною
функцією
 охоплена
ланкою з зворотнім зв’язком
охоплена
ланкою з зворотнім зв’язком
 .
.
Задача №7
Записати
частотні характеристики ланки з
передаточною функцією
 .
.
Задача №8
Знайти
вираз для передаточної функції замкнутої
системи, якщо передаточна функція
розімкнутої системи має вигляд

Задача №9
Записати
диференціальне рівняння ланки з
передаточною функцією
 Задача
№10
Задача
№10
Записати
диференціальне рівняння ланки з
передаточною функцією
 .
.
Задача №11
Записати характеристичне рівняння системи з передаточною функцією
 .
.
Задача №12
Знайдіть зображення за Лапласом для одиничної ступінчатої функції.
Задача №13
Знайти
еквівалентну передаточну функцію
паралельно узгодженого з’єднання двох
ланок, якщо їх передаточні функції
 і
і
 .
.
Задача №14
Записати
передаточну функцію ланки, якщо її
диференціальне рівняння має вигляд

Задача №15
Передаточна функція замкнутої системи
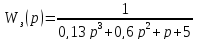
Оцініть стійкість системи за критерієм Гурвіца.
Задача №16
Чи стійка система, якщо характеристичне рівняння має вигляд
 .
.
Задача №17
Знайти передаточну функцію системи за помилкою, якщо передаточна функція розімкнутої системи

.
Задача №18
Знайти вираз для передаточної функції замкнутої системи, якщо передаточна функція розімкнутої системи має вигляд
 .
.
Задача №19
Записати рівняння для зв’язку між вхідною і вихідною величинами трипозиційного релейного елемента.
Задача №20
Нелінійна
система складається з ідеального
релейного елемента і неперервної частини
з передаточною функцією

Задача №21
Знайти критичний коефіцієнт передачі регулятора k, якщо характеристичне рівняння замкнутої системи має вигляд

Задача №22
Чи стійка система імпульсного керування, якщо характеристичне рівняння системи має вигляд

Задача №23
Знайти білінійне перетворення характеристичне рівняння імпульсної системи
 .
.
Література
Попович М.Г., Ковальчук О.В. Теорія автоматичного керування:
Підручник. – 2-ге вид., перероб. і доп. – К.: Либідь, 2007. – 656с.
Валюх О.А., Максимів В.М. Елементи теорії автоматичного
керування: Навчальний посібник. - Л.:Афіша, 2002. – 124с.
Автоматическое управление в химической промышленности:
Учебник для вузов(под ред. Е.Г.Дудникова).-М.:Химия, 1987,368с.
Шинки Ф. системи автоматического регулирования химико-
технологических процессов.-М.:Химия, 1974.-336с.
Автоматизация технологических процессов легкой промишлености:
Учебное пособие.(Под ред. Л.Н.Плужникова).-М.: Высшая Школа, 1984.-398с.
Трегуб В.Г. и др.. Автоматизация периодических процессов пищевой
промишлености.-М.: Агропромиздат, 1991.-352с.
Рэй У. Методы управления технологическими процессами. – М.:
Мир, 1988.-868с.
Стефани Е.П. Основы построения АСУТП.-М.: Энергия, 1982.-832с.
Балакирев В.С., Володин В.М., Цилин А.М. Оптимальное управление
процессами химической технологии. Экстремальные задачи АСУ.- М.: Химия, 1978.-384с.
Бояринов А.И., Кафаров В.В. Методы оптимизации в химической
технологии.- М.: Химия, 1971.
Салыга В.И. Автоматизированные системи управления
технологическими процессами.- Харьков: Высшая школа, 1976.
Липатов П.Н. Типовые процессы химической технологии как объекта
управления.- М.: Химия, 1973.-320с.
