
- •Технічний коледж
- •Методичні вказівки до виконання практичних робіт
- •Тема 1:Складання математичної моделі об’єкта керування
- •Тема 2: Типові ланки систем автоматичного керування
- •Тема 3: Способи з’єднання ланок та їх еквівалентні передаточні функції.
- •Послідовне з’єднання ланок
- •Паралельне з’єднання ланок
- •Тема 4: Амплітудні та фазові частотні характеристики елементарних ланок
- •Тема 5: Визначення стійкості. Алгебраїчні критерії стійкості. Критерії стійкості Гурвіца і Рауса.
- •Тема 6: Лінійна та квадратична інтегральні оцінки якості
- •Тема 8: Метод гармонічної лінеаризації (гармонічного балансу). Гармонічний коефіцієнт передачі нелінійного елемента.
- •Тема 9: Дискретні системи автоматичного керування
- •Завдання для самоконтролю:
Тема 8: Метод гармонічної лінеаризації (гармонічного балансу). Гармонічний коефіцієнт передачі нелінійного елемента.
Теоретичні відомості
На відміну від розглянутих раніше точних методів до нелінійних систем метод гармонічної лінеаризації, (гармонічного балансу) є наближеним. Ідею цього методу було запропоновано М. М. Криловим і М. М. Боголюбовим у 1934 р.
Метод
гармонічної лінеаризації використовується
для дослідження автоколивань у нелінійних
системах високого порядку, а також для
оцінки якості перехідних процесів,
зокрема для знаходження параметрів
автоколивань A
і
 .
.
G=0

 y(t)
y(t)










Рис. 8. Структурна схема найпростішої нелінійної САК
Автоколиванням називають стійкі гармонічні коливання, які виникають в нелінійних САК самостійно, без зовнішньої гармонічної дії.
Для
пояснення суті гармонічної лінеаризації
розглянемо проходження гармонічного
сигналу:
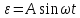 через нелінійну ланку (рис. 9).
через нелінійну ланку (рис. 9).


U U




b
0











0




 U
U
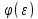


 Рис.
9.
Рис.
9.
На
виході нелінійної ланки в загальному
вигляді створюється періодичний сигнал
 .
.
де
 - амплітуда,
- амплітуда, – частота автоколивань.
– частота автоколивань.
Або якщо розкласти в ряд Фур’є:

Припустимо,
що
 ,
що справедливо для нелінійних
характеристик, симетричних відносно
початку координат, для вищої гармоніки
(k=1)
вираз запишеться у вигляді:
,
що справедливо для нелінійних
характеристик, симетричних відносно
початку координат, для вищої гармоніки
(k=1)
вираз запишеться у вигляді:
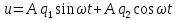
АЧХ
першої гармоніки значно більша інших,
тобто
 діє як низькочастотний фільтр, тобто у
цьому випадку нижчими гармоніками
нехтують.
діє як низькочастотний фільтр, тобто у
цьому випадку нижчими гармоніками
нехтують.


 –коефіцієнти
Фур’є
першої гармоніки.
–коефіцієнти
Фур’є
першої гармоніки.
Якщо перейти до зображень, то комплексна форма запису сигналів

(зображення Фур’є):

Отже,
нелінійна функція
 при
при
 замінюється лінійним виразом, ця операція
і називаєтьсягармонічною
лінеаризацією.
замінюється лінійним виразом, ця операція
і називаєтьсягармонічною
лінеаризацією.
Гармонічна лінеаризація по суті є наближеною. Вона ґрунтується на таких припущеннях:
у системі існують автоколивання;
коливання на вході нелінійної ланки є синусоїдальним, тобто лінійна
частина системи виконує функції фільтра основної гармоніки, це припущення прийнято називати гіпотезою фільтра.
Передаточна функція нелінійної ланки буде мати вигляд:
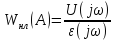
Передаточна
функція
 є передаточною функцією еквівалентної
лінійної ланки абогармонічною
передаточною функцією
нелінійної ланки.
є передаточною функцією еквівалентної
лінійної ланки абогармонічною
передаточною функцією
нелінійної ланки.
Або гармонічний коефіцієнт передач нелінійного елемента – це відношення зображення Фур’є першої гармоніки вихідного сигналу до зображення вхідного сигналу.
Можливий
інший запис, а саме:
 .
.
Задача
№1.
Знайти гармонічний коефіцієнт передачі
двопозиційного реле з гістерезисною
статичною характеристикою
 .
.

В

 -С
C
U
-С
C
U
B




U
U 



B
B


-C
0 C

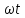

0




-B
-B 
0
A









З
рисунка видно, що
 ,
тоді
,
тоді
 .
.





Отже гармонічний коефіцієнт передачі двопозиційне резе з гістерезисною статичною характеристикою буде:

Задача №2. Методом гармонічної лінеаризації розрахувати параметри нелінійної системи.
Нехай задана гармонічно лінеаризована система, причому вхідний сигнал G=0.
G
E
U
Y









Застосуємо метод Гольдфарба:

Згідно
цього методу
 .
.
Лінійна частина системи задана інтегруючою ланкою ат інерційною 1-го порядку:



Задані
коефіцієнти: C=4B,
B=10B,
 ,
, .
.
Отже маємо:


На
комплексній площині будуємо годограф
АФЧХ лінійної частини нелінійної системи
і обернений гармонічний коефіцієнт
передачі при зміні амплітуди від 0 до
 .
Точка перетину двох графіків (-0,39;-0,31j).
.
Точка перетину двох графіків (-0,39;-0,31j).
Отже
амплітуда автоколивань буде А=0,39,
а фаза

