Алгоритми побудови моделей

Модель лінійної регресії (лінійне рівняння) є найпоширенішим видом залежності між економічними змінними.

Скористаймося методом найменших квадратів, суть якого полягає у наступному: сума квадратів відхилень ординат точки, що спостерігається (X_i, Y_i) від відповідної ординати точки, що лежить на регресійній прямій, повинна бути найменшою

Використання 1МНК для оцінки теоретичних параметрів моделі парної регресії приводить до таких систем нормальних рівнянь:

1. лінійна залежність Y = a₀ + a₁X.

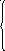
Побудоване лінійне рівняння може слугувати початковою точкою в разі складних (суттєво нелінійних) залежностей.

Нелінійні зв'язки, як правило, певними перетвореннями (заміною змінних чи логарифмуванням) зводять до лінійного вигляду або апроксимують (наближують) лінійними функціями.

б) гіперболічна залежність .Замінюємо і отримаємо лінійну модель Y = a₀ + a₁х′.

Для оцінки теоретичних параметрів моделі складаємо систему нормальних рівнянь:

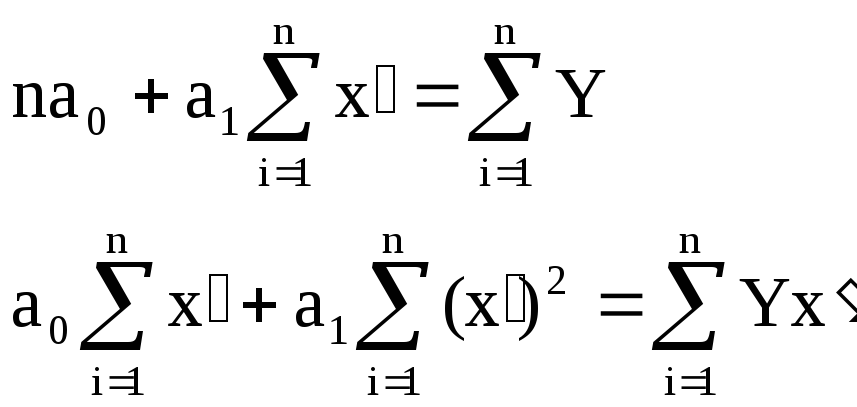
в) параболічна залежність Y = a₀ + a₁х² . Замінюємо х² = х′ і отримаємо лінійну модель Y = a₀ + a₁х′.

Для оцінки теоретичних параметрів моделі складаємо систему нормальних рівнянь:

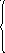
г) степенева залежність .

Логарифмуємо функцію lnY = ln a₀ + a₁ · ln Х.

Замінюємо логарифми lnY = Y′, ln Х = Х′ , ln a₀ = a′.

Одержуємо лінійну модель Y′ = a′+ a₁ · Х′.

Складаємо систему нормальних рівнянь:

д)експоненціальна .

Для оцінки теоретичних параметрів зводимо модель до лінійного вигляду:

Логарифмуємо функцію

Замінюємо логарифм

Одержуємо лінійну модель

е) проста модифікована експоненціальна

Методом заміни зводимо модель до лінійного вигляду:

Моделювання здійснюється на основі вибірки статистичних даних, яку студент отримує з відповідних таблиць.

Лабораторні роботи № 1, 2, 3, 4, 5 студент виконує згідно з завданням та варіантом вихідних даних, який отримує у викладача.

ДОДАТКОВО

Для спрощення проміжних розрахунків використаємо вбудовану в електронні таблиці Microsoft Excel статистичну функцію ЛИНЕЙН. Ця функція застосовує метод найменших квадратів, щоб визначити оцінки параметрів лінійної регресії.

ЛИНЕЙН (відомі_значення_Y; відомі_значення_Х; конст; ста­тистика).

Результат – це оцінка параметрів лінійної регресії та регресійна статистика.

Для цього треба:

1) відмітити поле, де буде знаходитись результат розміром (k+1)  5, або m₁  5; m₁ = k+1

2) ввійти у "майстер функцій f ". У категоріях вибираємо "статистична", а в функціях – ЛИНЕЙН. Вводимо адреси значень Y, Х та значення константи і статистики;

3) для того, щоб отримати на екрані результат, натискаємо спершу клавішу F2, а потім Ctrl+Shift+Еnter.

Функція може додатково обчислювати регресійну статистику (рис.1.1).

«Відомі значення Y» — множина значень Y. Якщо масив Y має один стовпець, то кожний стовпець масиву «відомі_значення_Х» інтерпретуються як окрема змінна. Якщо масив «відомі_значення_Y» має один рядок, то кожний рядок «відомих значень Х» інтерпретується як окрема змінна.

«Відомі_значення_Х» — множина значень Х, що враховує або одну (парна регресія), або кілька змінних (множинна регресія). Якщо «відомі_значення_Х» пропустили, то вважається, що це ма­сив {1; 2; 3;...} такого самого розміру, як n «відомих_значень Y».

«Конст» — логічне значення.

Якщо «конст» має значення «ложь», то ₀ беруть таким, що дорівнює нулю: значення  доби­рають так, щоб виконувалася рівність Y=ХА (модель без вільно­го члена).

Якщо «конст» має значення «истина», то ₀ обчислює­ться традиційно (модель з вільним членом).

«Статистика» — логічне значення, яке вказує, чи потрібно об­числювати додаткову статистику за регресією.

Якщо «статисти­ка» має значення «истина», то функція ЛИНЕЙН обчислює до­даткову регресійну статистику у вигляді масиву (див. рис. 1.1).

		…
		…
R2
F	Ступінь свободи n–m

Рис. 1.1. Статистика функції ЛИНЕЙН

де – оцінка параметра , j=1..k ;

– оцінка вільного члена регресії;

– стандартна похибка оцінки параметра a_і;

R² – коефіцієнт детермінації;

– стандартна похибка залишків;

F – F-критерій.

– середнє значення Y_факт .

Ступінь свободи дорівнює (n – m), де n – кількість спостере­жень, m – кількість змінних у моделі; це значення необхідне для визначення табличного значення F-критерію.

–сума квадратів відхилення, що пояснюється регресією;

– сума квадратів відхилення, що пояснюється по­хибкою u.

Якщо статистика має значення «ложь» чи її пропустили, то функція ЛИНЕЙН обчислює лише коефіцієнти a_j та константу a₀.