1.6. Формула Тейлора

В просторі візьмемо ортонормований базис, і розкладемо за ним вектор-функцію:.

Нехай функції в околі точки t₀ , мають скінченні похідні до -го порядку включно.

Для кожної скалярної функції ,,запишемо формулу Тейлора в околі точкиt₀ зі своїм залишковим членом та своєю проміжною точкою (i = 1,2,3):

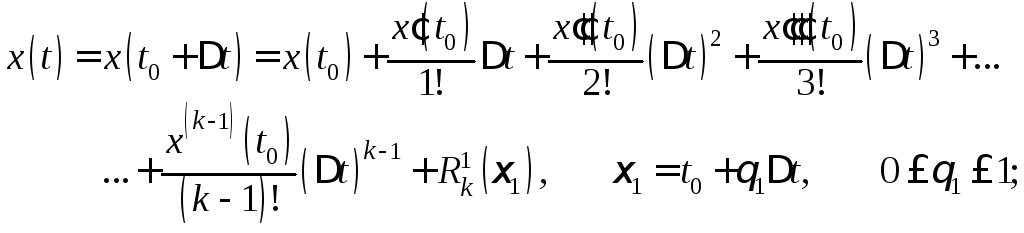
Помножимо рівності для ,,відповідно ната додамо:

Якщо має похідні довільного порядку, для неї можна скласти формальний ряд Тейлора в околі точкиt₀:

Не кожний формальний ряд Тейлора збігається.

Аналітичною вектор-функцією у точці називається функція, яка має в цій точці похідні будь-якого порядку та існує окіл точки t0 , в якому ряд Тейлора збігається до функції .

Позначення: – клас аналітичних функцій.

1.7. Інтеграл від вектор-функції

Невизначеним інтегралом від неперервної вектор-функції називається вектор-функціятака, що.

Ця функція визначається з точністю до сталого векторного доданка.

Визначеним інтегралом від неперервної вектор-функції на відрізкуназивається сталий вектор, що знаходиться за формулою Ньютона-Лейбніца:.

Основні властивості інтегралів зберігаються і для векторних функцій, а саме:

1°.

2°. ;

3°. якщо– сталий вектор;

4°. якщо– сталий вектор;

5°. ;

6°. якщо функціянеперервна на відрізкуі;

7°. .

1.8. Вектор сталої довжини

Нехай ,. Тоді , .

Диференціюючи останню рівність, дістанемо, що

, , .

Похідна вектор-функції сталої довжини ортогональна до самої вектор-функції при всіх значеннях аргументу.

Справджується й обернене твердження.

Контрольні питання до теми 1

1. Дайте означення вектор-функції одного скалярного аргументу. Що є областю визначення та областю значень вектор-функції?

2. Що називається годографом вектор-функції?

3. Наведіть означення нескінченно малого вектора, перелічіть та обгрунтуйте властивості нескінченно малих векторів.

4. Дайте означення границі вектор-функції. Сформулюйте та доведіть теореми про границі вектор-функцій.

5. Дайте означення вектор-функції, неперервної в точці; неперервної на відрізку.

6. Наведіть властивості вектор-функцій, неперервних на відрізку.

7. Наведіть означення похідної вектор-функції. Поясніть її геометричний та механічний зміст.

8. Яка функція називається диференційовною в точці? Сформулюйте та доведіть властивості диференційовних вектор-функцій.

9. Дайте означення невизначеного інтегралу від вектор-функції.

10. Що розуміють під визначеним інтегралом від вектор-функції?

11. Сформулюйте властивості інтегралу від вектор-функції.

12. Запишіть формулу Тейлора для вектор-функції скалярного аргументу.

13. Сформулюйте та доведіть необхідну і достатню умову того, щоб вектор-функція мала сталий модуль; мала сталий напрямок.

Тема 2. Поняття кривої. Регулярна крива і способи її задання

2.1. Поняття кривої

Поняття кривої є одним із основних в диференціальній геометрії. Спочатку цьому поняттю не давали точного математичного означення. Евклід (III ст.до н.е.) у своїх «Початках» називав лінією довжину без ширини або межу поверхні. Тривалий час уявлення про криву залишалось на наочному рівні. Прогрес в техніці вимагав точного означення кривої. Перше означення в досить загальній формі дозволив сформувати запропонований в 17 ст. Р. Декартом (1596-1650) метод координат. Так, плоскою кривою, яка визначається рівнянням із двома змінними стали називати множину точок на площині, координати яких задовольняють цьому рівнянню. Це рівняння називають загальним рівнянням лінії на площині. Однак уже в той час були відомі криві, які або взагалі не можна було задати рівнянням виду , де функціябула б достатньо простою, або ж це задання нічого не давало для вивчення лінії. Класичним прикладом такої кривої є спіраль Архімеда. (лінія, що описується точкою, яка рівномірно переміщується за променем, який, у свою чергу, обертається зі сталою кутовою швидкістю навколо нерухомої точки).

Для вивчення ліній, які є траєкторіями рухомої точки, найбільш природним є задання координат точки в залежності від часу. У зв’язку з цим з механіки виникло уявлення про криву як про траєкторію рухомої точки з координатами, які залежать від часу t. Згодом це привело до так званого параметричного задання лінії, коли координати її точок виражаються як функції деякої третьої змінної величини t (необов’язково часу), яку називають параметром. Найбільш чітке означення сформулював у другій половині 19 ст. К. Жордан (1838-1922): плоскою кривою називається сукупність точок площини, координати яких задовольняють рівнянням: , де φ і ψ є неперервними функціями аргументуt на деякому відрізку . Можна показати, що якщо функції φ і ψ визначені на іншому відрізку, то за допомогою лінійної підстановки можна перейти до відрізка[0,1], не порушуючи неперервності функцій φ і ψ. Інакше кажучи, плоска крива за Жорданом є образом відрізка [a,b] при неперервному відображенні на площину.

Це означення здавалось цілком відповідним наочному уявленню про криву, але в 1890 р. Д. Пеано (1858-1932) побудував неперервне відображення відрізка , образом якого є цілий квадрат на площині. Така крива проходить через усі точки квадрата.

Таким чином, означення Жордана виявилося, з одного боку, занадто широким, оскільки його умовам задовольняють криві, що не відповідають наочно-образним уявленням про криву. З іншого боку, воно дещо вузьке: наприклад, ним не охоплюється крива , 0 <; .

На кінець 19 століття в математику все глибше починає проникати теоретико-множинна точка зору, яка полягає в тому, що будь-який математичний об’єкт розглядається як множина тих чи інших елементів. Найбільш чітко теоретико-множинну точку зору сформулював Г. Кантор (1845-1918). Він визначив плоску криву як будь-яку зв’язну, компактну множину P точок площини, яка не містить в собі ніякої внутрішньої точки. Пояснимо терміни. Точка називається внутрішньою точкою множини, якщо разом з нею множині належить деякий її окіл. Граничною точкою множини М називається точка, в будь-якому околі якої є принаймні одна точка множини М, відмінна від цієї точки. Множина називається зв’язною, якщо при будь-якому поданні її у вигляді об’єднання двох непорожніх підмножин, які не мають спільних точок, принаймні в одній з цих підмножин знайдеться точка, гранична для іншої підмножини. Непорожня множина М називається компактною, якщо будь-яка її нескінченна підмножина містить хоч одну граничну точку множини М. Зв’язну компактну множину називають ще континуумом. Тому під канторовою кривою розуміють плоский континуум, у будь-якому околі кожної точки якого є точки, що не належать континууму.

Усі прості дуги і криві, що складаються з простих дуг, які не мають попарно спільних точок, окрім своїх кінців, відповідають умовам означення Кантора, а криві Пеано вже не є кривими за означенням Кантора.

Важливим прикладом канторової кривої є килим Серпінського.

Канторове означення не узагальнюється на просторові криві: в тривимірному просторі континуумом, який не містить внутрішніх точок, може бути не тільки крива, але й поверхня, наприклад, площина чи сфера.

Усі спроби математиків дати точне визначення кривої знайшли своє завершення в працях радянського математика П.С. Урисона (1898 – 1924). У 1921р. він, майже одночасно з австрійським математиком К.Менгером і незалежно від нього, дав найбільш загальне визначення поняття кривої, яким користуються в сучасній топології і яке придатне для будь-якого простору.

В диференціальній геометрії використовується дещо змінене означення Жордана. За основу береться поняття елементарної кривої, до вивчення якої зводиться дослідження будь-якої кривої в околі заданої точки, тобто «в малому».

Нехай – відображення інтервалу в евклідів простір(n=2,3): .

Множина , яка складається з образів усіх точок інтервалу при відображенні , називається образом інтервалу ; це деяка фігура .

Відображення φ називається топологічним відображенням, якщо воно неперервне; взаємно однозначне; обернене відображення є неперервним.

Нагадаємо означення використаних вище понять.

1. Відображення називаєтьсянеперервним в точці Х, якщо

,

тобто близькі точки з відображаються в близькі точки з.

Відображення називаєтьсянеперервним , якщо воно неперервне в кожній точці інтервалу .

2. Відображення називається взаємно однозначним, якщо в кожну точку відображається тільки одна точка з інтервалу .

3. Оберненим відображенням до відображення :називається відображеннятаке, що якщоХі, то.

Елементарною кривою називається образ інтервалу (a,b) при його топологічному відображенні в простір або на площину: –образ .

Приклад. Елементарною кривою є частина прямої або частина параболияк образи інтервалупри відповідних відображеннях. Коло, задане рівнянням, не є елементарною кривою.

Не всі елементарні криві є об’єктами диференціальної геометрії. Для того, щоб елементарна крива стала об’єктом диференціальної геометрії, потрібні додаткові умови, пов’язані з існуванням дотичної до кривої.

Простою кривою називається топологічний образ або відкритого відрізка прямої, або кола.

Проста крива в околі будь-якої своєї точки є елементарною.

Топологічний образ кола називається замкненою кривою.

Відображення множини в простір називається локально топологічним, якщо кожна точка цієї множини має окіл, в якому відображення є топологічним.

Загальною кривою називається множина точок простору, яка є образом простої кривої при локально топологічному відображенні її в простір.