Тема 4. Поняття теорії кривих, пов’язані з поняттями кривини та скруту

4.1. Довжина дуги кривої. Натуральна параметризація

Нехай просторову криву γ дано параметричним рівнянням і. Впишемо в кривуламану.

Ламана називаєтьсяправильно вписаною в криву , якщо її вершини на кривій слідують в тому ж порядку (тобто без зворотів) , що і їх прообрази на відрізку.

На відрізку візьмемо точкиНа кривій γ їм відповідають точкиСполучаючи послідовно ці точки, одержимо ламану, вписану в криву.

Розглянемо довжину цієї ламаної. Якщо кількість вершин ламаної збільшується, то її довжина збільшується. Справді, якщо на дузі кривої з кінцямиі взято нову вершину C, то сума прямолінійних відрізківібільша довжини прямолінійного відрізка. Тому довжина нової вписаної ламаноїбільша довжини ламаної.

Крива γ називається спрямною, якщо довжини всіх правильно вписаних в неї ламаних обмежені зверху. Верхня границя довжин усіх таких ламаних називається довжиною кривої і позначається.

Вона існує за теоремою Вейєрштраса.

Теорема 7. Гладка крива є спрямною. Довжина гладкої кривої() дорівнює визначеному інтегралу від модуля похідної: . (11)

В скалярній формі формула (11) має вид:

. (12)

Якщо криву задано рівняннями , то.

Для плоских кривих, розміщених у координатній площині, в цих формулах слід покласти.

Поняття довжини кривої дозволяє визначити на кривій параметр, який найбільш природнім способом пов’язаний з кривою. Таким параметром є довжина дуги. Дійсно, виберемо на кривій точкуі який-небудь напрямок на ній. Положення точкиB на кривій визначається її відстанню від точки . Приймемо за параметр на кривій довжинуs дуги , взяту зі знаком +, якщо дугамає додатній напрямок, і зі знаком – , якщо дугамає від’ємний напрямок.

Якщо до цього на прямій була інша параметризація і точці відповідало значення, а точціB – значення , то довжинаобчислюється за формулою:

, а отже , тобто є монотонною функцією від параметра і може бути прийнята за параметр. Цей параметр особливо зручний для вивчення кривої за її рівнянням і називаєтьсянатуральним параметром кривої. Така параметризація називається натуральною і позначається .

Для натуральної параметризації дотичний вектор кривої є одиничним вектором, тобто. Дійсно:.

Визначна властивість натуральної параметризації:

Якщо – натуральна параметризація , то. Навпаки, якщо для деякого параметра , то– довжина дуги.

4.2. Кривина кривої, заданої в натуральній параметризації

Напрям дотичної змінюється, якщо точка рухається по кривій. Щоб виміряти швидкість цієї зміни, візьмемо на кривійбудь-яку точкуP і точку Q, близьку до P. Проведемо дотичні в точках P і Q, знайдемо кут між ними і поділимо цей кут на довжину дуги PQ.

Позначимо:

–кут між дотичними до γ в точках P і Q, – довжина дугиPQ кривої γ.

Кривиною кривої γ в точці P називається границя відношення кута повороту дотичної на дузі, що стягується до даної точки, до довжини цієї дуги, тобто .

Вимірюючи швидкість зміни напряму дотичної, кривина показує, наскільки крива за своєю формою відхиляється від форми прямої лінії. Чим більша кривина, тим сильніше це відхилення. Очевидно, що для прямої лінії кривина дорівнює нулю в усіх її точках, бо напрямний вектор прямої не змінює свого напряму.

Для кола радіуса R:. Томунезалежно відQ. Отже, кривина кола є сталою і дорівнює, деR– радіус кола.

Вектор називаєтьсявектором кривини кривої. Його довжина дорівнює кривині кривої, заданої в натуральній параметризації.

Теорема 8. Регулярна крива класу (двічі неперервно диференційовна) має в кожній точці єдину кривину. Якщо – натуральна параметризація кривої, то кривина дорівнює модулю другої похідної функції:.

□Нехай точкам P і Q відповідають значення натурального параметра s і відповідно. Нехайі– одиничні дотичні вектори кривої в цих точках. Векторперенесемо паралельно так, щоб його початок співпадав з точкоюP. Кінці векторів іпозначимоM і N. ∆PMN – рівнобедрений, бо вектори і– одиничні.

, де L – середина відрізка MN.

З прямокутного трикутника PML, де :.

Поділимо обидві частини цієї рівності на і перейдемо до границі при.

Оскільки – двічі неперервно диференційовна крива і, то існує

,

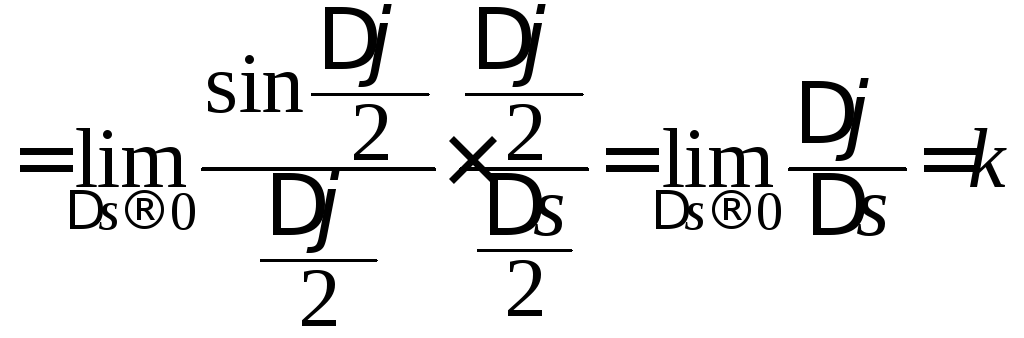бо при і границя першого множника дорівнює 1 (перша чудова границя). ■

Нехай в даній точці кривина . Розглянемовластивості вектора:

1) (оскільки– одиничний вектор і, отже);

2) належить стичній площині;

3) напрямлений за головною нормаллю іде– одиничний вектор головної нормалі. Останню рівність можна подати у виді:

(перша формула Френе). (13)