
- •Міністерство освіти і науки, молоді та спорту України
- •Програма курсу
- •Предмет диференціальної геометрії. Історичний огляд розвитку диференціальної геометрії
- •Тема 1. Вектор-функція скалярного аргументу
- •1.1. Операції над сталими векторами та їх застосування
- •1.2. Вектор-функція скалярного аргументу
- •1.3. Границя вектор-функції
- •1.4. Неперервність вектор-функції
- •1.5. Похідна вектор-функції
- •1.6. Формула Тейлора
- •1.7. Інтеграл від вектор-функції
- •1.8. Вектор сталої довжини
- •Контрольні питання до теми 1
- •Тема 2. Поняття кривої. Регулярна крива і способи її задання
- •2.1. Поняття кривої
- •2.2. Способи аналітичного задання просторової кривої
- •2.3. Випадок плоскої кривої
- •Контрольні питання до теми 2
- •Перелічіть способи аналітичного задання просторової кривої. Запишіть відповідні рівняння. Які умови є достатніми для того, щоб ці рівняння визначали регулярну криву?
- •Тема 3. Дотична пряма і супровідний тригранник кривої
- •3.1. Дотична пряма просторової кривої
- •3.2. Нормальна площина просторової кривої
- •3.3. Дотична і нормаль плоскої кривої
- •3.4. Стична площина кривої
- •3.5. Супровідний тригранник кривої
- •Контрольні питання до теми 3
- •Тема 4. Поняття теорії кривих, пов’язані з поняттями кривини та скруту
- •4.1. Довжина дуги кривої. Натуральна параметризація
- •4.2. Кривина кривої, заданої в натуральній параметризації
- •4.3. Кривина кривої в довільній параметризації
- •4.4. Кривина плоскої кривої
- •4.5. Скрут кривої, заданої в натуральній параметризації
- •4.6. Скрут кривої в довільній параметризації
- •4.7. Формули Френе
- •1. ; 2.; 3..
- •Контрольні питання до теми 4
- •Список використаної та рекомендованої літератури
- •Додаток 1 Питання для підготовки до вхідного контролю з навчальної дисципліни «Диференціальна геометрія та топологія»
- •Додаток 2
- •Завдання вхідного контролю з навчальної дисципліни
- •«Диференціальна геометрія та топологія»
- •Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 8
- •Варіант 9
- •Варіант 10
- •Додаток 3 Тестовий контроль з теорії кривих Тест 1. Вектор-функція скалярного аргументу
- •1. Вказати правильні відповіді із запропонованих. Якщо правильних відповідей декілька, перелічити їх усі.
- •2. Вставити пропущені слова так, щоб одержалось правильне твердження.
- •Тест 2. Поняття кривої. Регулярна крива і способи її задання
- •1. Вказати правильні відповіді із запропонованих. Якщо правильних відповідей декілька, перелічити їх усі.
- •Тест 3. Дотична пряма і супровідний тригранник кривої
- •1. Вказати правильні відповіді із запропонованих. Якщо правильних відповідей декілька, перелічити їх усі.
- •Пов’язані з поняттями кривини та скруту
- •1. Вказати правильні відповіді із запропонованих.
- •2. Вставити пропущені слова так, щоб одержалось правильне твердження.
- •Зоря Валентина Дмитрівна,
3.2. Нормальна площина просторової кривої
|
Нормаллю кривої в даній її точці називається пряма, яка проходить через цю точку і перпендикулярна до дотичної, проведеної до кривої у цій точці. |
Просторова крива має нескінченну множину нормалей. Усі вони лежать в одній площині, яка називається нормальною площиною.
|
Нормальною площиною кривої в даній її точці називається площина, яка проходить через дану точку і перпендикулярна до дотичної, проведеної до кривої у цій точці. |
Н ехай
ехай![]() – радіус-вектор довільної точкиM
нормальної площини
– радіус-вектор довільної точкиM
нормальної площини
![]() в точці
в точці
![]() .
.
Тоді
вектор
![]() є нормальним вектором площини
є нормальним вектором площини![]() :
:
![]() .
.
Відповідно
до способу задання кривої маємо такі
рівняння нормальної площини в точці
![]() :
:
![]() ;
(7)
;
(7)
![]() ;
(7')
;
(7')
 . (7")
. (7")
Задача.
Скласти рівняння дотичної прямої та
нормальної площини до кривої
 в точці
в точці
![]() .
.
Розв’язання.
![]() –рівняння
еліпсоїда;
–рівняння
еліпсоїда;
![]() –рівняння
параболоїда.
–рівняння
параболоїда.

При
![]() ;
;
![]() ;
;
![]() маємо:
маємо:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Отже:
 .
.
Рівняння дотичної прямої:
 ;
;
![]() ;
;
![]() .
.
Рівняння нормальної площини:
![]() ;
;
![]() .
.
Відповідь:
![]() ;
;
![]() .
.
3.3. Дотична і нормаль плоскої кривої
Якщо
крива плоска і розміщена в координатній
площині
![]() (
(![]() ),
легко отримати результати, подані нижче
в таблиці 1.
),
легко отримати результати, подані нижче
в таблиці 1.
Таблиця 1.
|
Рівняння кривої |
Рівняння дотичної прямої |
Рівняння нормальної прямої |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.4. Стична площина кривої
Порівняємо
радіус-вектор довільної точки дотичної
прямої
![]() з розкладом радіус-вектора кривої в
околі точки
з розкладом радіус-вектора кривої в
околі точки
![]()
![]() .
.
Якщо
покласти
![]() ,
то ці радіус-вектори відрізняються на
нескінченно малу
,
то ці радіус-вектори відрізняються на
нескінченно малу![]() :
:![]() Тому при досить малому
Тому при досить малому![]() криву
криву![]() можна наближено замінити на дотичну
пряму. Іншими словами, дотична пряма є
першим наближенням кривої. Це означає,
що властивості кривої можна вивчати
(«в малому») за допомогою простішого
геометричного образу – прямої (а саме:
дотичної прямої).
можна наближено замінити на дотичну
пряму. Іншими словами, дотична пряма є
першим наближенням кривої. Це означає,
що властивості кривої можна вивчати
(«в малому») за допомогою простішого
геометричного образу – прямої (а саме:
дотичної прямої).
Узагальненням цієї задачі є задача про знаходження площини, яка була б найтісніше пов’язана з кривою в даній її точці. Це так звана стична площина.
|
Стичною
площиною
кривої
|
Площина,
яка проходить через дотичну до кривої
![]() ,
називається дотичною площиною
,
називається дотичною площиною![]() .
Дотична площина до кривої
.
Дотична площина до кривої![]() проходить через дві точки
проходить через дві точки![]() ,
що необмежено зближуються (до
,
що необмежено зближуються (до![]() ).
Стична площина – та з дотичних площин,
яка проходить через три точки кривої
).
Стична площина – та з дотичних площин,
яка проходить через три точки кривої![]() , що необмежено зближуються.
, що необмежено зближуються.
Якщо
![]() – плоска крива, то її стична площина
співпадає з площиною, в якій лежить ця
крива.
– плоска крива, то її стична площина
співпадає з площиною, в якій лежить ця
крива.
Виведемо
рівняння стичної площини. Нехай крива
![]() задана рівнянням у векторній формі
задана рівнянням у векторній формі![]() .
Візьмемо на
.
Візьмемо на![]() точку
точку
![]() , якій відповідає радіус-вектор
, якій відповідає радіус-вектор
![]() :
:![]() . Проведемо в цій точці дотичну до
. Проведемо в цій точці дотичну до
![]() ,
напрям дотичної визначається вектором
,
напрям дотичної визначається вектором![]() .
.
Нехай
![]() – точка
– точка
![]() , близька до
, близька до
![]() ,
і точці
,
і точці
![]() відповідає радіус-вектор
відповідає радіус-вектор
![]() :
:![]() .
Через дотичну і точку
.
Через дотичну і точку![]() проведемо площину
проведемо площину![]() .
Довільній точці
.
Довільній точці![]() площини
площини![]() поставимо у відповідність радіус-вектор
поставимо у відповідність радіус-вектор![]() :
:![]() .
.
О скільки
вектори
скільки
вектори![]() ,
,![]() і
і![]() лежать в одній площині
лежать в одній площині![]() ,
то їх мішаний добуток дорівнює нулю:
,
то їх мішаний добуток дорівнює нулю:![]() .
.
Але
![]() ;
;![]() .
.
Звідси
![]() .
(8)
.
(8)
Знайдемо
розклад Тейлора для функції
![]() .
Для цього запишемо розклад для
радіуса-вектора кривої
.
Для цього запишемо розклад для
радіуса-вектора кривої![]() в околі точки
в околі точки
![]() за степенями
за степенями
![]() :
:
![]() .
.
Звідси
![]() .
.
Підставимо
![]() в (8). Одержимо:
в (8). Одержимо:
 ;
;
 .
.
Врахуємо,
що
![]() ,
і поділимо обидві частини останньої
рівності на
,
і поділимо обидві частини останньої
рівності на![]() .
.
Одержимо
![]() . (9)
. (9)
Для
стичної площини
![]() (за означенням) , тому
(за означенням) , тому![]() .
.
Тоді з (9) одержимо рівняння стичної площини у векторній формі :
![]() . (10)
. (10)
|
Теорема
6.
В будь-якій точці регулярної кривої
класу
1)
якщо
2)
якщо
|
Враховуючи, що

можемо записати (10) в скалярній формі:
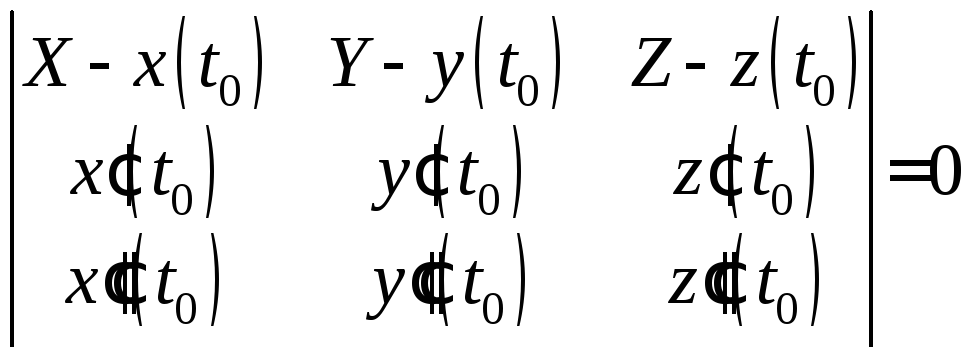 .
(10')
.
(10')
Основні властивості стичної площини
|
1°. Стична площина кривої є граничним положенням площини, яка проходить через три нескінченно близькі точки кривої. Прийнявши цю властивість за означення стичної площини, можна отримати її рівняння. 2°.Дотичною площиною кривої називається будь-яка площина, що проходить через дотичну пряму. Площини, що дотикаються до кривої в даній точці, утворюють пучок. Стична площина належить цьому пучку і є однією з дотичних площин. Можна з’ясувати відмінність стичної площини від інших дотичних площин, які називатимемо звичайними дотичними площинами. Якщо точка кривої наближається до точки дотику, то: 1) віддаль її від звичайної дотичної площини є нескінченно мала другого порядку відносно приросту параметра; 2) віддаль точки від стичної площини є нескінченно мала, принаймні, третього порядку відносно того ж приросту параметра.
3°.Стична
площина має дотикання другого порядку
з кривою, тобто:
Зауважимо, що дотична пряма з кривою має дотикання 1 порядку. Прийнявши цю властивість за означення стичної площини, можна довести теорему 6. 4°. При будь-якій параметризації кривої вектор другої похідної радіуса-вектора кривої розміщений в її стичній площині.
Якщо
t
– час, а
Вектор прискорення завжди розміщений в стичній площині траєкторії рухомої точки. |
Задача. Скласти рівняння стичної площини конічної гвинтової лінії
 в
початку координат.
в
початку координат.
Розв’язання.
Початок координат відповідає значенню
![]() .
Знайдемо перші та другі похідні поt:
.
Знайдемо перші та другі похідні поt:

При
![]() маємо:
маємо:


Підставляємо ці значення в рівняння (10'):
 ,
звідки
,
звідки
![]() ,
тобто
,
тобто![]()
Зауваження.
Дана лінія називається конічною,
оскільки вона розміщена на конусі
![]() .
Це легко перевірити підстановкою:
.
Це легко перевірити підстановкою:![]() .
.
Відповідь:
![]()



