Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ»

Домашняя работа

по дисциплине

“Статистика”

Выполнила студентка Просенкова Наталья

очной формы обучения

специальности

Мировая экономика

курса 2 группы 2

Преподаватель:

Агеева Наталья Константиновна

Москва 2008

№	№ предприятия	Cреднее значение стоимости активов банков за квартал (Xi), млн. руб.	Прибыль банков за квартал (Yi), млн. руб.
1	1	625,04	16,01
2	2	629,27	15,87
3	3	630,88	16,12
4	4	640,99	17,60
5	5	663,36	17,79
6	6	663,83	17,69
7	7	671,75	17,02
8	9	677,16	16,99
9	10	698,74	19,07
10	11	710,84	18,31
11	12	728,57	18,66
12	14	742,17	18,64
13	15	742,33	18,86
14	16	755,13	19,76
15	19	771,05	19,06
16	20	774,81	19,91
17	21	775,49	19,80
18	22	783,05	20,08
19	25	817,76	20,33
20	26	820,35	21,86
21	27	828,00	21,42
22	28	831,67	21,61
23	29	836,73	21,49
24	33	859,75	21,35
25	34	860,83	21,87
26	35	870,58	21,53
27	37	881,16	22,83
28	38	888,17	23,23
29	39	904,58	22,74
30	40	906,13	22,78

Проверим однородность совокупности по величине факторного признака (X_i), подсчитав коэффициент вариации.

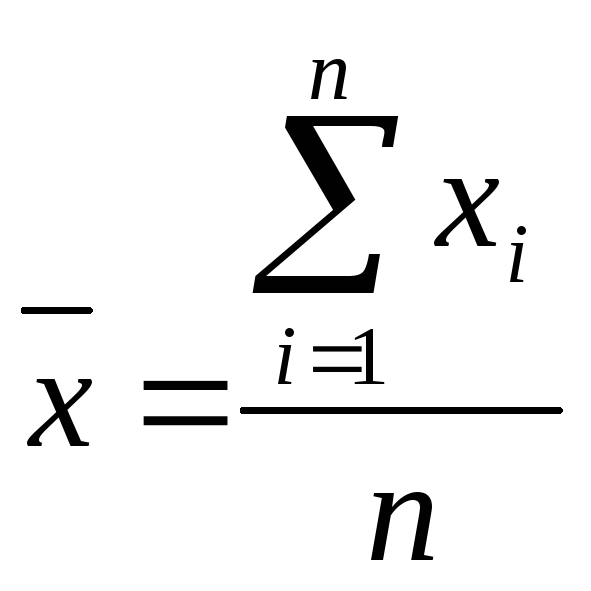= ≈ 766,439

=

=

= %

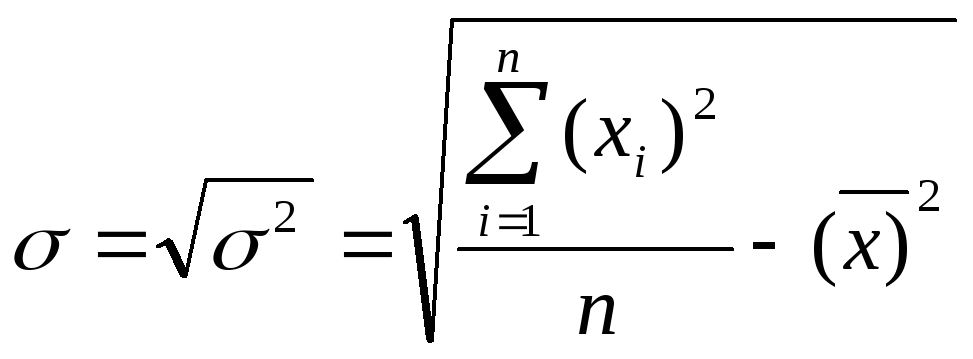Вывод: коэффициент вариации <33%, следовательно, совокупность качественно однородна.

2. Произвести группировку компаний по стоимости активов с целью выявления зависимости между размером компании по стоимости активов и прибыли. Результаты представить в виде статистической таблицы, сформулировать выводы.

Чтобы произвести группировку, воспользуемся формулой Стерджесса, приняв m равным 5:

=

Группы банков по размеру стоимости активов, млн.руб.	Число банков	Стоимость активов в группе, млн.руб.	Прибыль в группе, млн.руб.	Средняя прибыль по группе, млн.руб.	Относит. величина наглядности, %
625,04 – 681,26	8	5202,28	135,09	16,89	75,64
681,26 – 737,48	3	2138,15	56,04	18,68	83,65
737,48 – 793,7	7	5344,03	136,11	19,44	87,06
793,7 – 849,92	5	4134,51	106,71	21,34	95,57
849,92 – 906,14	7	6171,2	156,33	22,33	100
Итого	30	22990,17	590,28	-	-

Вывод: с увеличением стоимости активов компании прибыль увеличивается.

3. Построить ряд распределения компаний по прибыли, рассчитав величину интервала по формуле Стерджесса. Для построенного ряда определить среднюю прибыль, модальное и медианное значение прибыли, а также показатели вариации и формы распределения. Сформулировать выводы.

Количество групп: m = 1 + 3,322lg(n) =1+3,322 lg(30)=1+3,322*1,477= 5,906 ≈ 6

1) Рассчитаем величину интервала по формуле Стерджесса:

= 1,13 ≈ 1,5

2) Построим ряд распределения:

Группы банков по прибыли за квартал, x	Число банков, f	Накопленная частота
15 – 16,5	3	3
16,5 – 18	5	8
18 – 19,5	6	14
19,5 – 21	5	19
21 – 22,5	8	27
22,5 - 24	3	30
итого	30	-

3) Средняя величина прибыли

=

4) Мода:

Мода лежит в интервале (21 – 22,5), так как на него падает наибольшая частота 8.

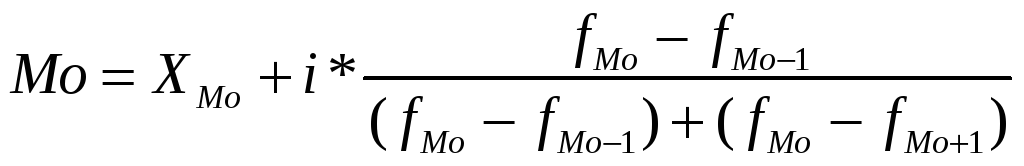=21+1,5* =

= 21 + 1,5*0,375 = 21,56

Вывод: наиболее часто встречающееся значение прибыли предприятия составляет 21,56 млн. руб.

5) Медиана:

Найдем интервал, в котором лежим медиана:

= 15, 5 - следовательно, медиана лежит в интервале (19,5 – 21)

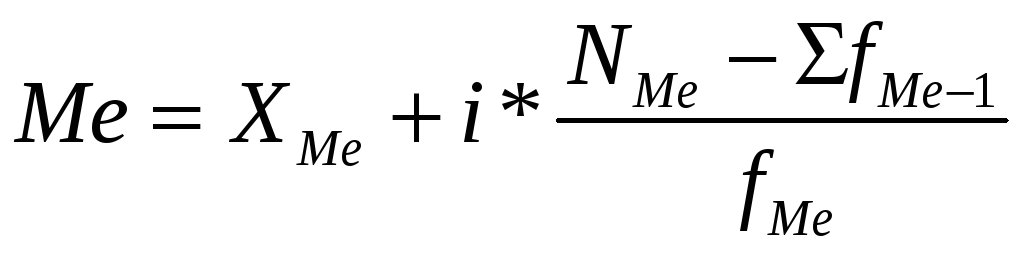= 19,5 + 1,5*= 19,95

Вывод: 19,95 млн. руб. – это значение прибыли банков за квартал, которое лежит в середине ранжированного ряда и делит его на 2 равные части.

6) Показатели вариации.

Абсолютные:

1. Размах колебаний:

R= Xmax-Xmin = 23,23 – 15,87 = 7,36

2. Среднее линейное отклонение:

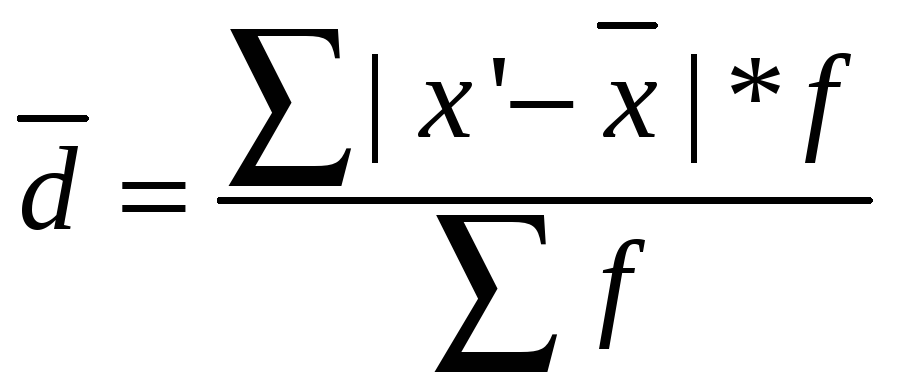= (|15,75–19,7|*3 + |17,25–19,7|*5 + |18,75–19,7|*6 + |20,25–19,7|*5 +

+ |21,75–19,7|*8 + |23,25–19,7|*3)/30 = (11,85 + 12,25 + 5,7 + 2,75 + 16,4 + 10,65)/30 = 1,986

3. Среднее квадратичное отклонение:

2,278

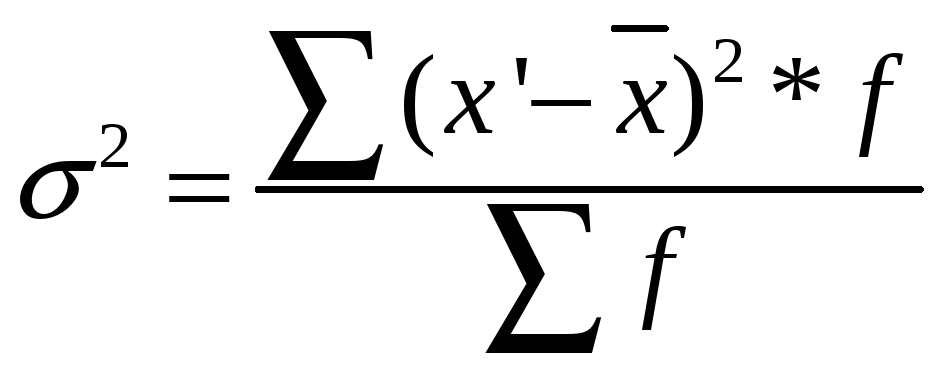= (15,84*3 + 6*5 + 0,9*6 + 0,3*5 + 4,20*8 + 12,6*3)/30 = 5,19

Относительные:

1. Относительный размах колебаний

= %

2. Относительное линейное отклонение

=

3. Коэффициент вариации

=

7) Показатели формы распределения:

1. Показатель асимметрии

=

Вывод: величина показателя асимметрии положительна, следовательно, асимметрия правосторонняя. Так как её значение по модулю >0,25 , то асимметрия значительная.

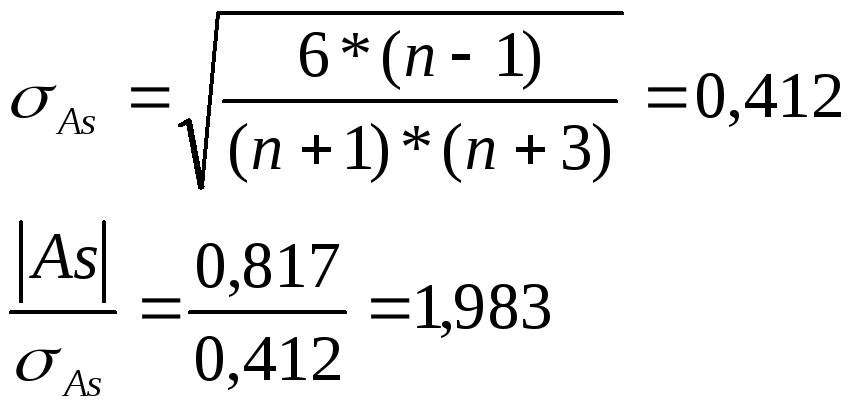
2. Показатель эксцесса

Ex=

51,117

Ex = 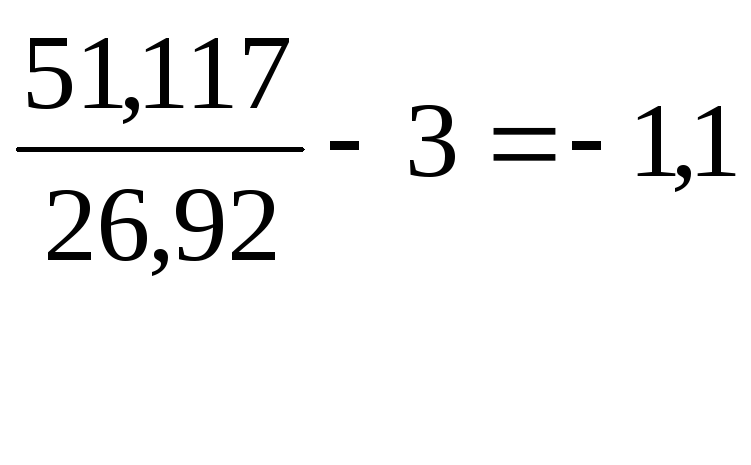распределение туповершинно

- эксцесс не существенен, значит распределение нормально.

4. Используя ранее выполненную группировку компаний по стоимости активов (пункт 2), проверить правило сложения дисперсий по объему прибыли.

Группы банков по размеру стоимости активов, млн.руб.	Число банков	Прибыль в группе, млн.руб.	Средняя прибыль по группе, млн.руб.	Относит. величина наглядности, %
625,04 – 681,26	8	135,09	16,89	75,64
681,26 – 737,48	3	56,04	18,68	83,65
737,48 – 793,7	7	136,11	19,44	87,06
793,7 – 849,92	5	106,71	21,34	95,57
849,92 – 906,14	7	156,33	22,33	100
Итого	30	590,28	-	-