Банк тестових завдань

для поточного, проміжного та модульного контролю знань З КУРСУ «НАРИСНА ГЕОМЕТРІЯ»

1. Основоположниками нарисної геометрії є:

а) [ ] Олександр Хаскін;

b) [ ] Володимир Гордон;

c) [ ] Віктор Виноградов;

d) [ ] Гаспар Монж.

2. Проеціюванням називають:

а) [ ] процес побудови проекцій на площині;

b) [ ] зображення геометричної фігури у проекційному зв’язку;

c) [ ] процес побудови креслень у системі прямокутних проекцій;

d) [ ] наочне зображення геометричної фігури.

3. Який метод є основою нарисної геометрії:

а) [ ] координатний метод;

b) [ ] метод проекціювання;

c) [ ] метод аксонометрій;

d) [ ] метод перспективи.

4. Яким методом користуються для побудови зображень предметів на площині?

а) [ ] методом аксонометричних проекцій;

b) [ ] методом проекціювання;

c) [ ] методом допоміжних січних площин;

d) [ ] методом обертання.

5. Для забезпечення достатньої наочності складних об’єктів застосовують:

а) [ ] аксонометричні зображення;

b) [ ] прямокутні проекції;

c) [ ] перспективні зображення;

d) [ ] центральні проекції.

6. За способом проекціювання проекції називають:

а) [ ] центральними;

b) [ ] паралельними;

c) [ ] перпендикулярними;

d) [ ] косокутними.

7. Проекція – це зоображення предмета, «відкинуте» на площину при допомозі:

а) [ ] точок;

b) [ ] прямих;

c) [ ] променів;

d) [ ] слідів.

8. Спроекціювати предмет на площину – це значить побудувати його:

а) [ ] проекції на площині;

b) [ ] відображення на площині;

в) [ ] зображення на площині;

d) [ ] аксонометричну проекцію.

9. Якщо кут нахилу проекціювальних променів до площини проекцій не дорівнює 90⁰, то спосіб проекціювання називається:

а) [ ] паралельним;

b) [ ] перпендикулярним;

c) [ ] прямокутним;

d) [ ] косокутним.

10. Якщо проекціювальні промені перпендикулярні до площини проекцій, то спосіб проекціювання називається:

а) [ ] паралельним;

b) [ ] перпендикулярним;

c) [ ] прямокутним;

d) [ ] косокутним.

11. Центральними проекціями називають:

а) [  ] проекції, одержані проецюючими променями перпедикулярними до площини проекцій;

b) [  ] проекції, одержані проецюючими променями, які перетинаються в одній точці;

c) [  ] проекції, одержані паралельними проецюючими променями;

d) [  ] наочне зображення геометричної фігури.

12. Паралельними проекціями називають:

а) [  ] проекції одержані проецюючими променями, перпедикулярними до площини проекцій

b) [  ] проекції одержані проецюючими променями, які перетинаються в одній точці

c) [  ] проекції одержані паралельними проецюючими променями

d) [  ] наочне зображення геометричної фігури.

13. Прямокутними проекціями називають:

а) [  ] проекції одержані проецюючими променями, перпедикулярними до площини проекцій

b) [  ] проекції одержані проецюючими променями, які перетинаються в одній точці

c) [  ] проекції одержані паралельними проецюючими променями

d) [  ] наочне зображення геометричної фігури.

14. Яке твердження лежить в основі прямокутного проеціювання?

a) [ ] Центр проеціювання – власна точка, проецюючі промені – прямі лінії, поверхня зображення – площина.

b) [ ] Центр проеціювання – невласна точка, проецюючі промені – прямі, перпендикулярні до площини зображення.

c) [ ] Центр проеціювання – власна точка, проецюючі промені – лінії,. поверхня зображення – циліндрична поверхня.

d) [ ] Центр проеціювання – невласна точка, проецюючі промені утворюють гострий кут з площиною проекцій.

15. Яке твердження лежить в основі косокутного проеціювання?

a) [ ] Центр проеціювання – невласна точка, проецюючі промені – прямі, перпендикулярні до площини зображення.

b) [ ] Центр проеціювання – власна точка, проецюючі промені – лінії,. поверхня зображення – циліндрична поверхня.

c) [ ] Центр проеціювання – невласна точка, проецюючі промені – криві лінії, поверхня зображення – площина.

d) [ ] Центр проеціювання – невласна точка, проецюючі промені утворюють гострий кут з площиною проекцій.

16. На які види поділяються паралельні проекції:

а) [ ] центральні;

b) [ ] прямокутні;

c) [ ] косокутні;

d) [ ] аксонометричні.

17. Що означає вираз: ?

а) [ ] проекцією прямої l є пряма l_i;

b) [ ] проекцією точки А є точка А_i;

c) [  ] якщо точка А належить прямій l, то проеція точки А належить одноіменній проекції прямої l;

d) [ ] якщо пряма l є проецюючою, то її проекцією є точка А.

18. Що означає вираз ?

а) [ ] якщо пряма (АВ) паралельна прямій (СD), то їх одноіменні проекції теж паралельні;

b) [  ] проекції, одержані на паралельних площинах рівні між собою;

c) [  ] відношення відрізків паралельних прямих дорівнює відношенню їх проекцій;

d) [  ] при паралельному проеціюванні зберігається просте відношення довжин відрізків прямої.

19. Що означає вираз

а) [  ] якщо пряма (АВ) паралельна прямый (СD), то їх одноіменні проекції теж паралельні;

b) [  ] проекції, одержані на паралельних площинах рівні між собою;

c) [  ] відношення відрізків паралельних прямих дорівнює відношенню їх проекцій;

d) [  ] при паралельному проеціюванні зберігається просте відношення довжин відрізків прямої.

20. Що означає вираз

а) [  ] якщо пряма (АВ) паралельна прямій (СD), то їх одноіменні проекції теж паралельні;

b) [  ] проекції, одержані на паралельних площинах рівні між собою;

c) [  ] відношення відрізків паралельних прямих дорівнює відношенню їх проекцій;

d) [  ] при паралельному проеціюванні зберігається просте відношення довжин відрізків прямої.

21. Що означає вираз

а) [  ] якщо пряма (АВ) паралельна прямій (СD), то їх одноіменні проекції теж паралельні;

b) [  ] проекції, одержані на паралельних площинах рівні між собою;

c) [  ] відношення відрізків паралельних прямих дорівнює відношенню їх проекцій;

d) [  ] при паралельному проеціюванні зберігається просте відношення довжин відрізків прямої.

22. Що означає вираз

а) [  ] якщо пряма (АВ) паралельна прямій (СD), то їх одноіменні проекції теж паралельні;

b) [  ] проекції, одержані на паралельних площинах рівні між собою;

c) [  ] відношення відрізків паралельних прямих дорівнює відношенню їх проекцій;

d) [  ] довжина проекцій відрізка дорівнює довжині відрізка в просторі, помноженому на косинус кута, якого утворює відрізок з площиною проекцій.

23. Що означає вираз

а) [  ] проекції, одержані на паралельних площинах рівні між собою;

b) [  ] якщо одна сторона прямого кута паралельна площині проекції, то проекцією цього кута є прямий кут;

c) [  ] відношення відрізків паралельних прямих дорівнює відношенню їх проекцій;

d) [  ] довжина проекцій відрізка дорівнює довжині відрізка в просторі, помноженому на косинус кута якого утворює відрізок з площиною проекцій.

24. В нарисній геометрії вивчати способи побудови зображень геометричних форм за їх складовими елементами, починають з:

а) [ ] точки;

b) [ ] прямої;

c) [ ] площини;

d) [ ] геометричного тіла.

25. Що називають геометричною фігурою:

а) [ ] довільну множину точок;

b) [ ] довільну множину прямих;

c) [ ] довільну множину площин;

d) [ ] довільну множину відрізків.

26. Вкажіть геометричну фігуру:

а) [ ] точка;

b) [ ] відрізок;

c) [ ] трикутник;

d) [ ] пряма;

27. Побудова проекцій геометричних елементів ґрунтується на методі:

а) [ ] координатному;

b) [ ] проекціювання;

c) [ ] аксонометрій;

d) [ ] перспективи.

28. Перетин проекціювального променя з площиною проекцій дає проекцію:

а) [ ] точки;

b) [ ] прямої;

c) [ ] площини;

d) [ ] фігури.

29. Три взаємно перпендикулярні площини проекцій утворюють:

а) [ ] три площини проекції;

b) [ ] трьохгранний кут;

c) [ ] двогранний кут;

d) [ ] картинну площину.

30. Основними площинами проекцій є:

а) [ ] горизонтальна та фронтальна;

b) [ ] фронтальна та профільна;

c) [ ] горизонтальна, фронтальна та загального положення;

d) [ ] горизонтальна, фронтальна та профільна.

31. Яке взаємне розташування основних площин проекцій:

а) [ ] паралельні між собою;

b) [ ] суміщені з фронтальною площиною проекції;

c) [ ] розташування залежить від напрямку проеціювання;

d) [ ] взаємно перпендикулярні.

32. Яку з трьох площин проекцій вважають нерухомою:

а) [ ] П₁;

b) [ ] П₂;

c) [ ] П₃;

d) [ ] горизонтальну.

33. Як одержують комплексне креслення?

а) [  ] горизонтальну та фронтальну площини суміщують з профільною площиною;

b) [  ] профільну та фронтальну площини суміщують з горизонтальною площиною

c) [  ] горизонтальну та профільну площини суміщують з фронтальною площиною;

d) [  ] проеціюванням геометричної фігури разом з координатними осями на площину проекції.

34. Лінії взаємного перетину площин проекцій називаються

а) [ ] проекціювальними променями;

b) [ ] осями проекцій;

c) [ ] лініями зв’язку;

d) [ ] лініями перетину.

35. Як називається площина проекцій П₁:

а) [ ] горизонтальна;

b) [ ] фронтальна;

c) [ ] профільна;

d) [ ] вертикальна.

36. Як називається площина проекцій П₂:

а) [ ] горизонтальна;

b) [ ] фронтальна;

c) [ ] профільна.

d) [ ] вертикальна.

37. Як називається площина проекцій П₃:

а) [ ] горизонтальна;

b) [ ] фронтальна;

c) [ ] профільна;

d) [ ] вертикальна.

38. Як називається лінія перетину двох площин проекцій П₁ та П₂:

а) [ ] Ох;

b) [ ] Оу;

в) [ ] Оz;

d) [ ] фронтальним слідом.

39. Як називається лінія перетину двох площин проекцій П₂ та П₃:

а) [ ] Ох;

b) [ ] Оу;

c) [ ] Оz;

d) [ ] профільним слідом.

40. Як називається лінія перетину двох площин проекцій П₁ та П₃:

а) [ ] Ох;

b) [ ] Оу;

c) [ ] Оz;

d) [ ] горизонтальним слідом.

41. Проекції точки мають таку властивість:

а) [  ] фронтальна та горизонтальна проекції точки належать одній вертикальній лінії зв’язку;

в) [  ] фронтальна та горизонтальна проекції точки належать одній горизонтальній лінії зв’язку;

с) [  ] фронтальна та горизонтальна проекції точки належать одній лінії зв’язку;

d) [  ] фронтальна та горизонтальна проекції точки не належать одній лінії зв’язку.

42. Відстань від горизонтальної проекції точки до осі Х_1,2 є її:

а) [ ] ординатою;

b) [ ] аплікатою;

c) [ ] абсцисою;

d) [ ] проекцією.

43. Відстань від фронтальної проекції точки до осі Х_1,2 є її:

а) [ ] ординатою;

b) [ ] аплікатою;

c) [ ] абсцисою;

d) [ ] довжиною.

44. Висота точки визначається її відстанню від:

а) [ ] горизонтальної площини проекцій;

b) [ ] фронтальної площини проекцій;

c) [ ] профільної площини проекцій;

d) [ ] початку координат.

45. Широта точки визначається її відстанню від:

а) [ ] горизонтальної площини проекцій;

b) [ ] фронтальної площини проекцій;

c) [ ] профільної площини проекцій;

d) [ ] початку координат.

46. Глибина точки визначається її відстанню від:

а) [ ] горизонтальної площини проекцій;

b) [ ] фронтальної площини проекцій;

c) [ ] профільної площини проекцій;

d) [ ] вісі ОХ.

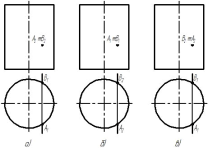
47. Яка з точок знаходиться в площині проекцій П₁?

а) [ ] К; b) [ ] L; c) [ ] M; d) [ ] N.

48. Яка з точок знаходиться в площині проекцій П₂?

а) [ ] К; b) [ ] L; c) [ ] M; d) [ ] N.

49. Яка з точок знаходиться в площині проекцій П₃?

а) [ ] К; b) [ ] L; c) [ ] M; d) [ ] N.

50. Яка з точок знаходиться в на вісі О_х?

а) [ ] К; b) [ ] L; c) [ ] M; d) [ ] N.

51. Якими координатами задають точку, яка лежить в площині проекцій П₁:

а) [ ] х, у, z;

b) [ ] х, у;

c) [ ] х, z;

d) [ ] у, z.

52. Якими координатами задають точку, яка лежить в площині проекцій П₂:

а) [ ] х, у, z;

b) [ ] х, у;

c) [ ] х, z;

d) [ ] у, z.

53. Якими координатами задають точку, яка лежить в площині проекцій П₃:

а) [ ] х, у, z;

b) [ ] х, у;

c) [ ] х, z;

d) [ ] у, z.

54. Відстань від точки до площини проекцій П₁ вимірюється координатою:

а) [ ] Ох;

b) [ ] Оу;

c) [ ] Оz;

d) [ ] ХУ.

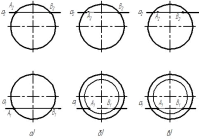
55. Яка з точок знаходиться в І четверті:

а) [ ] A; b) [ ] B; c) [ ] C; d) [ ] D.

56. Яка з точок знаходиться в ІI четверті:

а) [ ] A; b) [ ] B; c) [ ] C; d) [ ] D.

57. Яка з точок знаходиться в ІIІ четверті:

а) [ ] A; b) [ ] B; c) [ ] C; d) [ ] D.

58. Яка з точок знаходиться в ІV четверті:

а) [ ] A; b) [ ] B; c) [ ] C; d) [ ] D.

59. Де знаходиться точка з координатами (35, -60, 0):

а) [ ] у ІІ чверті;

b) [ ] у просторі;

c) [ ] у ІІІ чверті;

d) [ ] на площині.

60. Які із заданих точок знаходяться в просторі:

а) [ ] А (0, 20, 40);

b) [ ] В (0, 35, 0);

c) [ ] С (15, 15, 0);

d) [ ] D (25, 25, 25).

61. Які із заданих точок знаходяться на вісі О_у:

а) [ ] А (0, 20, 40);

b) [ ] В (0, 35, 0);

c) [ ] С (15, 15, 0);

d) [ ] D (25, 25, 25).

62. Які із заданих точок лежать на площині проекцій П₁:

а) [ ] А (0, 20, 40);

b) [ ] В (0, 35, 0);

c) [ ] С (15, 15, 0);

d) [ ] D (25, 25, 25).

63. Горизонтальна А₁ і фронтальна А₂ проекції точки завжди розташовані на:

а) [ ] вертикальній лінії зв’язку, яка перпендикулярна до осі проекцій О_х;

b) [ ] вертикальній лінії зв’язку, яка перпендикулярна до осі проекцій О_у;

c) [ ] горизонтальній лінії зв’язку, яка перпендикулярна до осі проекцій О_х;

d) [ ] горизонтальній лінії зв’язку, яка перпендикулярна до осі проекцій О_z.

64. Як називається лінія А₂А₃:

а) [ ] проекціювальна лінія;

b) [ ] горизонтальна лінія зв’язку;

c) [ ] вертикальна лінія зв’язку;

d) [ ] постійна пряма креслення.

65. Як називається лінія А₁А₂:

а) [ ] проекціювальна лінія;

b) [ ] лінія зв’язку;

c) [ ] вертикальна лінія зв’язку;

d) [ ] постійна пряма креслення.

66. Задані точки А(45, 20, 80), В(30, 60, 40), С(80, 45, 10). Яка з цих точок розташована найближче до площини проекцій П₁:

а) [ ] А;

b) [ ] В;

c) [ ] С;

d) [ ] жодна.

67. Задані точки А(45, 20, 80), В(30, 60, 40), С(80, 45, 10). Яка з цих точок розташована найближче до площини проекцій П₂:

а) [ ] А;

b) [ ] В;

c) [ ] С;

d) [ ] жодна.

68. Задані точки А(45, 20, 80), В(30, 60, 40), С(80, 45, 10). Яка з цих точок розташована найближче до площини проекцій П₃:

а) [ ] А;

b) [ ] В;

c) [ ] С;

d) [ ] жодна.

69. Задані точки А(45, 20, 80), В(30, 60, 40), С(80, 45, 10). Яка з цих точок розташована найдальше від площини проекцій П₁:

а) [ ] А;

b) [ ] В;

c) [ ] С;

d) [ ] жодна.

70. Задані точки А(45, 20, 80), В(30, 60, 40), С(80, 45, 10). Яка з цих точок розташована найдальше від площини проекцій П₂:

а) [ ] А;

b) [ ] В;

c) [ ] С;

d) [ ] жодна.

71. Задані точки А(45, 20, 80), В(30, 60, 40), С(80, 45, 10). Яка з цих точок розташована найдальше від площини проекцій П₃:

а) [ ] А;

b) [ ] В;

c) [ ] С;

d) [ ] жодна.

72. Вкажіть місце розташування точки з координатами (0, 60, 30):

а) [ ] у І чверті;

b) [ ] у просторі;

c) [ ] у ІІІ чверті;

d) [ ] на площині.

73. Вкажіть місце розташування точки з координатами (0, 0, 30):

а) [ ] у І чверті;

b) [ ] у просторі;

c) [ ] на вісі;

d) [ ] на площині.

74. Положення точки в просторі визначається, як мінімум:

а) [ ] однією проекцією;

b) [ ] двома проекціями;

c) [ ] трьома проекціями;

d) [ ] жодною.

75. Задані точки А(45, 20, 45), В(30, 45, 45), С(45, 45, 10). Яка з цих точок рівновіддалена від площин проекцій П₁ і П₂:

а) [ ] А;

b) [ ] В;

c) [ ] С.

d) [ ] жодна.

76. Задані точки А(45, 20, 45), В(30, 45, 45), С(45, 45, 10). Яка з цих точок рівновіддалена від площин проекцій П₁ і П₃:

а) [ ] А;

b) [ ] В;

c) [ ] С;

d) [ ] жодна.

77. Задані точки А(45, 20, 45), В(30, 45, 45), С(45, 45, 10). Яка з цих точок рівновіддалена від площин проекцій П₂ і П₃:

а) [ ] А;

b) [ ] В;

c) [ ] С;

d) [ ] жодна.

78. Вкажіть умову належності точки площині проекцій П₂:

а) [ ] Х≠0, У≠0, Z≠0;

b) [ ] Х≠0, У=0, Z≠0;

c) [ ] Х≠0, У≠0, Z=0;

d) [ ] Х≠0, У≠0, Z≠0.

80. Яка з точок рівновіддалена від площини проекцій П₁ і П₃:

а) [ ] А(15, 40,40);

b) [ ] В(15, 15, 40);

c) [ ] С(15, 40, 15);

d) [ ] жодна.

81. За допомогою конкуруючих точок визначають:

а) [ ] видимість пар геометричних елементів;

b) [ ] взаємне розташування геометричних елементів у просторі;

c) [ ] взаємне розташування прямих;

d) [ ] взаємне розташування площин.

82. Точки, що належать (інциденті) одній проекціювальній прямій, називають:

а) [ ] точками сходу слідів;

b) [ ] точками видимості;

c) [ ] конкуруючими;

d) [ ] координатами точки.

83. Точка задана координатами X, Y, Z, відстань від точки до горизонтальної площини проекцій визначається координатою:

а) [ ] Х;

b) [ ] Y;

c) [ ] Z;

d) [ ] Y, Z.

84. Точка А задана координатами X, Y, Z. Відстань від точки до горизонтальної площини проекцій визначається на епюрі відстанню:

а) [ ] А_хА₂;

b) [ ] А_хА₁;

c) [ ] А_хА₃;

d) [ ] А₁А₂;.

85. Вкажіть умову належності точки простору:

а) [ ] Х≠0, У≠0, Z≠0;

b) [ ] Х≠0, У=0, Z≠0;

c) [ ] Х≠0, У≠0, Z=0;

d) [ ] Х=0, У=0, Z=0.

86. Якою координатою визначається відстань від точки до площини проекцій П₁:

а) [ ] Х;

b) [ ] У;

c) [ ] Z;

d) [ ] горизонтальною.

87. Як називається пряма при допомозі, якої будують третю проекцію точки:

а) [ ] проекціювальна лінія;

b) [ ] лінія зв’язку;

c) [ ] вертикальна лінія зв’язку;

d) [ ] постійна пряма креслення.

88. Проекцією точки є:

а) [ ] точка;

b) [ ] пряма;

c) [ ] площина;

d) [ ] слід.

89. Вкажіть які з точок розташовані в просторі:

а) [ ] А, В, С, Е; b) [ ] А, В, Е, Д, F; c) [ ] А, В, С, Д; d) [ ] F, Е.

90. Які знаки мають координати Y і Z , якщо точка розташована І чверті простору:

а) [ ] +, +;

b) [ ] -, +;

c) [ ] -, -;

d) [ ] +, -.

91. Які знаки мають координати Y і Z , якщо точка розташована ІІ чверті простору:

а) [ ] +, +;

b) [ ] -, +;

c) [ ] -, -;

d) [ ] +, -.

92. Які знаки мають координати Y і Z , якщо точка розташована ІІІ чверті простору:

а) [ ] +, +;

b) [ ] -, +;

c) [ ] -, -;

d) [ ] +, -.

93. Які знаки мають координати Y і Z , якщо точка розташована ІV чверті простору:

а) [ ] +, +;

b) [ ] -, +;

c) [ ] -, -;

d) [ ] +, -.

94. Якщо координати Y і Z деякої точки однакові за величиною із знаком «+», то ця точка рівновіддалена від площин проекцій і розташована у:

а) [ ] у просторі;

b) [ ] у парній бісекторній площині;

c) [ ] у непарній бісекторній площині;

d) [ ] у непарній бісекторній площині І четверті.

95. Вкажіть які з точок лежать в площині проекцій:

а) [ ] А, В, С, Е; b) [ ] А, В, Е, Д, F; c) [ ] А, В, С, Д; d) [ ] F, Е.

96. Скільки вказано точок на кресленні:

а) [ ] 4; b) [ ] 5; c) [ ] 8; d) [ ] 9.

97. Яка з точок лежить на площині проекцій П₃:

а) [ ] А; b) [ ] С; c) [ ] М; d) [ ] К.

98. Вкажіть умову належності точки вісі Оу:

а) [ ] Х≠0, У=0, Z≠0;

b) [ ] Х=0, У≠0, Z=0;

c) [ ] Х≠0, У=0, Z=0.

d) [ ] Х≠0, У≠0, Z≠0.

99. Вкажіть умову належності точки вісі Оz:

а) [ ] Х=0, У=0, Z≠0;

b) [ ] Х≠0, У=0, Z≠0;

c) [ ] Х≠0, У=0, Z=0;

d) [ ] Х≠0, У≠0, Z=0.

100. Вкажіть умову належності точки вісі Ох:

а) [ ] Х≠0, У=0, Z≠0;

b) [ ] Х=0, У=0, Z≠0;

c) [ ] Х≠0, У=0, Z=0.

d) [ ] Х≠0, У≠0, Z≠0.

101. Скільки точок зображено на епюрі:

а) [ ] 7; b) [ ] 6; c) [ ] 12; d) [ ] 20.

102. До якої з площин проекцій точка А (15, 30, 55) знаходиться найближче:

а) [ ] П₁;

b) [ ] П₂;

c) [ ] П₃.

d) [ ] Ох.

103. Вкажіть умову належності точки площині проекцій П₃:

а) [ ] Х=0, У≠0, Z≠0;

b) [ ]Х≠0, У=0, Z≠0;

c) [ ]Х≠0, У≠0, Z=0;

d) [ ] Х=0, У=0, Z≠0.

104. До якої з площин проекцій точка А (15, 5, 55) знаходиться найближче:

а) [ ] П₁;

b) [ ] П₂;

c) [ ] П₃;

d) [ ] Ох.

105. Вкажіть яка з точок розташована в ІІ четверті простору:

а) [ ] А; b) [ ] В; c) [ ] С; d) [ ] Е.

106. Зображення трьох площин проекцій разом із зображеними на них проекціями А₁, А₂, А₃ точки А називають:

а) [ ] наочним зображенням;

b) [ ] комплексним кресленням точки;

c) [ ] перспективою;

d) [ ] аксонометричною проекцією.

107. Вказати умову належності точки площині проекцій П₁:

а) [ ] Х≠0, У≠0, Z≠0;

b) [ ] Х≠0, У=0, Z≠0;

c) [ ] Х≠0, У≠0, Z=0;

d) [ ] Х≠0, У=0, Z=0.

108. Вказати місце розташування заданих на епюрі точок:

а) [ ] А – І ч.; В – ІІ ч.; С – І ч.; Д – ІІІ ч.; Е – ІІІ ч.; F – ІV ч.

b) [ ] А – ІV ч.; В – І ч.; С – І ч.; Д – І ч.; Е – ІІІ ч.; F – ІІ ч.

c) [ ] А – ІІ ч.; В – І ч.; С – ІV ч.; Д – ІІІ ч.; Е – І ч.; F – ІV ч.

d) [ ] А – ІV ч.; В – І ч.; С – І ч.; Д – ІІІ ч.; Е – ІІІ ч.; F – ІV ч.

109. Фронтальна А₂ і профільна А₃ проекції точки завжди розташовані на:

а) [ ] вертикальній лінії зв’язку, яка перпендикулярна до осі проекцій О_х;

b) [ ] вертикальній лінії зв’язку, яка перпендикулярна до осі проекцій О_у;

c) [ ] горизонтальній лінії зв’язку, яка перпендикулярна до осі проекцій О_х;

d) [ ] горизонтальній лінії зв’язку, яка перпендикулярна до осі проекцій О_z.

110. Горизонтальна А₁ і фронтальна А₂ проекції точки завжди розташовані на:

а) [ ] вертикальній лінії зв’язку, яка перпендикулярна до осі проекцій О_х;

b) [ ] вертикальній лінії зв’язку, яка перпендикулярна до осі проекцій О_у;

c) [ ] горизонтальній лінії зв’язку, яка перпендикулярна до осі проекцій О_х;

d) [ ] горизонтальній лінії зв’язку, яка перпендикулярна до осі проекцій О_z.

111. Пряму, яка з’єднує дві проекції точки на комплексному кресленні, називають:

а) [ ] лінією перетину;

b) [ ] вісю проекцій;

c) [ ] лінією зв’язку;

d) [ ] постійною лінією креслення.

112. На якому рисунку вірно побудовано епюр точки F за даним наочним зображенням:

a) [ ]

b) [ ]

c) [ ]

d) [ ]

113. На якому рисунку вірно побудовано епюр точки L за даним наочним зображенням?

a) [ ]

b) [ ]

c) [ ]

d) [ ]

114. На якому рисунку вірно побудовано епюр точки E за даним наочним зображенням?

a) [ ]

b) [ ]

c) [ ]

d) [ ]

115. У прямокутній системі координат точка К має координати (20;10;30). Точка з якими координатами симетрична точці К відносно початку координат:

a) [ ] A (20;-10;-30);

b) [ ] B (-20;10;-30);

c) [ ] C (-20;-10;-30);

d) [ ] D (-20;-10;30).

116. У прямокутній системі координат точка К має координати (20;10;30). Точка з якими координатами симетрична точці K відносно площини проекцій П1?

a) [ ] A (20;10;-30);

b) [ ] В (-20;10;-30);

c) [ ] С (20;-10;-30);

d) [ ] D (20;-10;30).

117. У прямокутній системі координат точка К має координати (20;10;30). Точка з якими координатами симетрична точці K відносно площини проекцій П2?

a) [ ] A (20;-10;-30);

b) [ ] B (20;10;-30);

c) [ ] С (-20;10;-30);

d) [ ] D (-20;-10;30).

118. У прямокутній системі координат точка К має координати (20;10;30). Точка з якими координатами симетрична точці K відносно площини проекцій П3?

a) [ ] A (-20;10;30);

b) [ ] B (20;-10;-30);

c) [ ] C (-20;-10;-30);

d) [ ] D (20;10;-30).

119. У прямокутній системі координат точка К має координати (20;10;30). Точка з якими координатами симетрична точці K відносно осі x1,2?

a) [ ] A (20;-10;-30);

b) [ ] B (-20;10;-30);

c) [ ] C (-20;-10;-30);

d) [ ] D (20;10;-30).

120. У прямокутній системі координат точка К має координати (20;10;30). Точка з якими координатами симетрична точці K відносно осі y_1,3?

a) [ ] A (20;-10;-30);

b) [ ] B (-20;10;30);

c) [ ] C (-20;-10;-30);

d) [ ] D (-20;10;-30).

121. У прямокутній системі координат точка К має координати (20;10;30). Точка з якими координатами симетрична точці K відносно осі z_2,3?

a) [ ] A (20;-10;-30);

b) [ ] В (-20;10;-30);

c) [ ] С (-20;-10;30);

d) [ ] D (20;10;-30).

122. Якою цифрою на рисунку позначено горизонтальну проекцію предмета?

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] 1,2.

123. Якою цифрою на рисунку позначено фронтальну проекцію предмета?

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] 1,2.

124. Якою цифрою на рисунку позначено профільну проекцію предмета?

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] 1,3.

125. Якою цифрою на рисунку позначено горизонтальну площину проекцій?

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] Х1.

126. Якою цифрою на рисунку позначено фронтальну площину проекцій?

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] У1.

127. Якою цифрою на рисунку позначено профільну проекцію предмета?

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] жодною.

128. На якому рисунку вірно побудовано епюр точки K за даним наочним зображенням?

a) [ ] 1;

b) [ ] 2;

c) [ ] 3;

d) [ ] 4.

129. На якому рисунку вірно побудовано епюр точки D за даним наочним зображенням?

a) [ ] 1;

b) [ ] 2;

c) [ ] 3;

d) [ ] 4.

130. На якому рисунку вірно побудовано епюр точки H за даним наочним зображенням?

a) [ ] 1;

b) [ ] 2;

c) [ ] 3;

d) [ ] 4.

131. На якому рисунку вірно побудовано епюр точки А за даним наочним зображенням?

a) [ ] 1;

b) [ ] 2;

c) [ ] 3;

d) [ ] 4.

132. На якому рисунку вірно побудовано епюр точки B за даним наочним зображенням?

a) [ ] 1;

b) [ ] 2;

c) [ ] 3;

d) [ ] 4.

133. На якому рисунку вірно побудовано епюр точки C за даним наочним зображенням?

a) [ ] 1;

b) [ ] 2;

c) [ ] 3;

d) [ ] 4.

134. Аксонометричне зображення це:

а) [  ] наочне зображення об’єкта, пов’язане з прямокутною системою координат;

b) [  ] наочне зображення об’єкта, пов’язане з косокутною системою координат;

c) [  ] наочне зображення об’єкта, пов’язане з системою координат;

d) [  ] наочне зображення об’єкта.

135. Залежно від кута нахилу проецюючих променів до аксонометричної площини розрізняють:

a) [ ] прямокутну та центральну аксонометрію;

b) [ ] прямокутну та косокутну аксонометрію;

c) [ ] паралельну та центральну аксонометрію;

d) [ ] паралельну та ортогональну аксонометрію.

136. Як називають аксонометрію, якщо показники спотворення по всіх осях одинакові?

a) [ ] диметрією;

b) [ ] ізометрією;

c) [ ] триметрією;

d) [ ] тригонометрією.

137. Як називають аксонометрію, якщо показники спотворення по всіх осях різні диметрією?

a) [ ] ізометрією;

b) [ ] диметрією;

c) [ ] триметрією;

d) [ ] тригонометрією.

138. Як називається аксонометрична проекція, у якій кут між осями OX, OY, OZ дорівнює 120 град.?

a) [ ] косокутна фронтальна диметральна проекція;

b) [ ] прямокутна проекція;

c) [ ] прямокутна ізометрична проекція;

d) [ ] прямокутна диметрична проекція.

139. Як відкладати координати точок в аксонометрії?

a) [ ] тільки перпендикулярно відповідним вісям XYZ;

b) [ ] тільки по вісям XYZ;

c) [ ] тільки паралельно вісям XYZ;

d) [ ] не паралельно вісям XYZ або паралельно їм.

140. Які кути між аксонометричними вісями ХYZ у прямокутній ізометрії?

a) [ ] 120⁰, 120⁰, 120⁰;

b) [ ] 135⁰, 135⁰, 90⁰;

c) [ ] 150⁰, 120⁰, 90⁰;

d) [ ] 135⁰, 90⁰, 135⁰.

141. Які приведені коефіцієнти спотворення по осях XYZ в прямокутній диметрії?

a) [ ] р=1, q=1, r=0,5;

b) [ ] р=0,5, q=1, r=0,5;

c) [ ] р=1, q=1, r=1;

d) [ ] р=1, q=0,5, r=1.

142. Як проектується коло в стандартній аксонометрії?

a) [ ] параболою;

b) [ ] колом;

c) [ ] гіперболою;

d) [ ] еліпсом.

143. Чому дорівнюють приведені коефіцієнти спотворення по осях XYZ в прямокутній ізометрії?

a) [ ] р=0,5, q=1, r=0,5;

b) [ ] р=1, q=2, r=3;

c) [ ] р=0,5, q=0,5, r=0,5;

d) [ ] р=1, q=1, r=1.

144. Для побудови кола в прямокутній ізометрії потрібно накреслити допоміжний ромб з довжиною сторони, що дорівнює

a) [ ] радіусу кола;

b) [ ] діаметру кола;

c) [ ] довжині кола;

d) [ ] діаметру чи довжині кола;

145. Які коефіцієнти спотворення використовуються для побудови предмета в косокутній фронтальній диметрії?

a) [ ] р=1, q=0,5, r=1;

b) [ ] р=1, q=1, r=0,5;

c) [ ] р=0,5, q=0,5, r=0,5;

d) [ ] р=1, q=1, r=1.

146. Які кути між аксонометричними осями ХYZ у фронтальній диметрії?

a) [ ] 135⁰, 135⁰, 90⁰;

b) [ ] 120⁰, 120⁰, 120⁰;

c) [ ] 135⁰, 90⁰, 135⁰;

d) [ ] 90⁰, 135⁰, 135⁰.

147. Чим відрізняється фронтальна ізометрія від прямокутної ізометрії?

a) [ ] кутами між вісей;

b) [ ] розташуванням вісей та коефіцієнтами спотворення;

c) [ ] напрямком проекціювання;

d) [ ] кутами між вісями та напрямком проекціювання.

148. Як поділяються аксонометричні проекції залежно від співвідношення коефіцієнтів спотворення ?

a) [ ] прямокутна диметрія, прямокутна диметрія, триметрія;

b) [ ] аксонометрія, ізометрія, диметрія;

c) [ ] фронтальна ізометрія, горизонтальна ізометрія;

d) [ ] ізометрія, диметрія, триметрія.

149. Чим відрізняється прямокутна аксонометрія від косокутної ?

a) [ ] напрямком вісей;

b) [ ] кутами між вісями;

c) [ ] напрямком проекціювання;

d) [ ] кутами між вісями та коефіцієнтами спотворення.

150. Яка відмінність натуральних коефіцієнтів спотворення від приведених?

a) [  ] приведені коефіцієнти спотворення використовують для диметрії, натуральні – для ізометрії;

b) [  ] натуральні коефіцієнти спотворення є округленими значеннями приведених;

c) [  ] приведені коефіцієнти спотворення використовують для ізометрії, натуральні – для диметріїї;

d) [  ] приведені коефіцієнти спотворення є округленими значеннями натуральних.

151. Що називається аксонометрією?

a) [ ] вигляд зліва зверху;

b) [ ] вигляд зверху;

c) [ ] натуральна величина;

d) [ ] наочне зображення.

152. Наочні зображення предметів потрібні для:

a) [ ] вирішення метричних та позиційних задач;

b) [ ] доповнення уявлення про об’єкт зображення;

c) [ ] вивчення стандартів креслення;

d) [ ] вирішення метричних задач.

153. За якою ознакою розділяють аксонометрії на прямокутні та косокутні?

a) [ ] за напрямком вісей;

b) [ ] з за коефіцієнтами спотворення по вісям;

c) [ ] за кутом між вісями X та Z;

d) [ ] за напрямком проекціювання.

154. Які кути між аксонометричними вісями XYZ для косокутної горизонтальної ізометрії?

a) [ ] 135⁰, 135⁰, 90⁰;

b) [ ] 90⁰, 120⁰, 150⁰;

c) [ ] 150⁰, 120⁰, 90⁰;

d) [ ] 135⁰, 90⁰, 135⁰.

155. Що таке коефіцієнт спотворення в аксонометрії?

a) [  ] відношення довжини відрізка по вісі Х до довжини відрізка по вісі Y;

b) [  ] відношення довжини аксонометричної проекції до натуральної довжини відрізка;

c) [  ] відношення натуральної довжини відрізка до довжини його аксонометричної проекції;

d) [  ] відношення довжини відрізка по вісі Y до довжини відрізка по вісі Z.

156. Сільки видів стандартних аксонометрій?

a) [ ] сім;

b) [ ] три;

c) [ ] чотири;

d) [ ] п’ять.

157. Розташування прямої в просторі визначається:

a) [ ] двома точками, через які вона проходить;

b) [ ] площиною, в якій вона розташована;

c) [ ] точкою, через яку вона проходить;

d) [ ] точкою, через яку вона проходить і напрямком.

158. Як розташовані прямі загального положення відносно основних площин проекцій:

a) [ ] перпендикулярно до однієї з основних площин проекцій;

b) [ ] паралельно до однієї з основних площин проекцій;

c) [ ] не паралельно до жодної з основних площин проекцій;

d) [ ] паралельно до напрямку проеціювання.

159. Як розташовані прямі рівня відносно основних площин проекцій:

a) [ ] перпендикулярно до однієї з основних площин проекцій;

b) [ ] паралельно до однієї з основних площин проекцій;

c) [ ] не паралельно до жодної з основних площин проекцій;

d) [ ] паралельно до напрямку проеціювання.

160. Як розташовані проецюючі прямі відносно основних площин проекцій:

a) [ ] перпендикулярно до однієї з основних площин проекцій;

b) [ ] паралельно до однієї з основних площин проекцій;

c) [ ] не паралельно до жодної з основних площин проекцій;

d) [ ] паралельно до напрямку проеціювання.

161. Як називається пряма, паралельна до горизонтальної площини проекції?

a) [ ] горизонтально проецюючою прямою;

b) [ ] фронтально проецюючою прямою;

c) [ ] горизонтальною прямою;

d) [ ] прямою загального положення.

162. Як називається пряма, перпендикулярна до горизонтальної площини проекції?

a) [ ] горизонтально проецюючою прямою;

b) [ ] фронтально проецюючою прямою;

c) [ ] горизонтальною прямою;

d) [ ] прямою загального положення.

163. Як називається пряма, паралельна до фронтальної площини проекції?

a) [ ] фронтально проецююча пряма;

b) [ ] профільна пряма;

c) [ ] горизонтально проецююча пряма;

d) [ ] фронтальна пряма.

164. Як називається пряма, перпендикулярна до фронтальної площини проекції?

a) [ ] фронтально проецююча пряма;

b) [ ] профільна пряма;

c) [ ] горизонтально проецююча пряма;

d) [ ] фронтальна пряма.

165. Як називається пряма, паралельна до профільної площини проекції?

a) [ ] фронтально проецююча пряма;

b) [ ] профільна пряма;

c) [ ] горизонтально проецююча пряма;

d) [ ] фронтальна пряма.

166. Як називається пряма, перпендикулярна до профільної площини проекції?

a) [ ] фронтально проецююча пряма;

b) [ ] профільно проецююча;

c) [ ] горизонтально проецююча пряма;

d) [ ] фронтальна пряма.

167. Проецюючою прямою називають:

a) [ ] лінію, яка проходить через дану точку;

b) [ ] лінію, перпендикулярну до площини проекцій;

c) [ ] лінію, яка проходить через дану точку у заданому напрямку;

d) [ ] лінію, паралельну до площини проекцій.

168. Як називається відрізок А₁В₁:

а) [ ] горизонтальна проекція відрізка АВ;

b) [ ] фронтальна проекція відрізка АВ;

c) [ ] профільна проекція відрізка АВ;

d) [ ] вертикальна лінія зв’язку.

169. Як називається відрізок А₂В₂:

а) [ ] горизонтальна проекція відрізка АВ;

b) [ ] фронтальна проекція відрізка АВ;

c) [ ] профільна проекція відрізка АВ;

d) [ ] горизонтальна лінія зв’язку.

170. Як називається відрізок А₃В₃:

а) [ ] горизонтальна проекція відрізка АВ;

b) [ ] фронтальна проекція відрізка АВ;

c) [ ] профільна проекція відрізка АВ.

d) [ ] постійна лінія креслення.

171. Перетин прямої з площиною П₁ називають:

а) [ ] горизонтальним слідом;

b) [ ] фронтальним слідом;

c) [ ] профільним слідом;

d) [ ] вертикальною лінією зв’язку.

172. Перетин прямої з площиною П₂ називають:

а) [ ] горизонтальним слідом;

b) [ ] фронтальним слідом;

c) [ ] профільним слідом;

d) [ ] вертикальним слідом.

173. Перетин прямої з площиною П₃ називають:

а) [ ] горизонтальним слідом;

b) [ ] фронтальним слідом;

c) [ ] профільним слідом;

d) [ ] вісі ОУ.

174. Як називається пряма:

а) [ ] горизонтально-проецююча пряма; b) [ ] фронтально-проецююча пряма; c) [ ] горизонтальна пряма; d) [ ] пряма загального положення.

175. Як називається пряма:

а) [ ] фронтально-проецююча пряма; b) [ ] профільна пряма; c) [ ] горизонтально-проецююча пряма; d) [ ] фронтальна пряма.

176. Як називається пряма:

а) [ ] фронтально-проецююча пряма; b) [ ] профільна пряма; c) [ ] горизонтально-проецююча пряма; d) [ ] фронтальна пряма.

177. Як називається пряма:

а) [ ] фронтально-проецююча пряма; b) [ ] профільна пряма; c) [ ] горизонтально-проецююча пряма; d) [ ] фронтальна пряма.

178. Як називається пряма:

а) [ ] фронтально-проецююча пряма; b) [ ] профільна пряма; c) [ ] горизонтально-проецююча пряма; d) [ ] фронтальна пряма.

179. Як називається пряма:

а) [ ] фронтально-проецююча пряма; b) [ ] профільно-проецююча пряма; c) [ ] горизонтально-проецююча пряма; d) [ ] фронтальна пряма.

180. Яка точка невидима на горизонтальній площині проекції:

а) [ ] А; b) [ ] В; c) [ ] С; d) [ ] D.

181. Яка точка невидима на фронтальній площині проекції:

а) [ ] А; b) [ ] В; c) [ ] С; d) [ ] D.

182. Якщо пряма паралельна площині проекцій, то відрізок прямої зображується на одній із площин проекцій:

а) [ ] в спотвореному вигляді;

b) [ ] в натуральну величину;

c) [ ] в точку;

d) [ ] в відрізок.

183. Якщо пряма перпендикулярна до площини проекцій, то вона проекціюється в:

а) [ ] спотвореному вигляді;

b) [ ] натуральну величину;

c) [ ] точку;

d) [ ] початок координат.

184. Якщо пряма не паралельна і не перпендикулярна до жодної з площин проекцій, то відрізок прямої зображується на всі площини проекцій в:

а) [ ] спотвореному вигляді;

б) [ ] натуральну величину;

c) [ ] точку;

d) [ ] постійна пряма креслення.

185. Прямі, паралельні площинам проекцій, називають:

а) [ ] лініями загального положення;

b) [ ] лініями рівня;

c) [ ] проекціювальними лініями;

d) [ ] вертикальними лініями зв’язку.

186. Визначте довжину просторової ламаної лінії АВСDEF:

а) [ ] мм; b) [ ] см; c) [ ] мм; d) [ ] см.

187. Прямі, перпендикулярні до площин проекцій, називають:

а) [ ] лініями загального положення;

b) [ ] лініями рівня;

c) [ ] проекціювальними лініями;

d) [ ] лініями окремого положення.

188. Якщо однойменні проекції прямих на кресленні перетинаються і проекції їх точки перетину лежать на одній лінії зв’язку, то дві прямі в просторі:

а) [ ] взаємо паралельні;

b) [ ] перерехресні;

c) [ ] мимобіжні;

d) [ ] перпендикулярні.

189. Прямі, не паралельні жодній з площин проекцій, називають:

а) [ ] лініями загального положення;

b) [ ] лініями рівня;

c) [ ] проекціювальними лініями;

d) [ ] лініями окремого положення.

190. Якщо дві прямі в просторі не паралельні між собою і не перетинаються, то вони:

а) [ ] проекціювальні прямі;

b) [ ] прямі рівня;

c) [ ] мимобіжні;

d) [ ] перпендикулярні.

191. Прямі окремого положення можуть бути:

а) [ ] загальними та паралельними прямими;

b) [ ] прямими рівня і проекціювальними прямими;

c) [ ] прямими рівня та загальними прямими.

d) [ ] перехресними прямими.

192. Положення прямої в просторі однозначно визначається сукупністю:

а) [ ] однієї її проекції;

b) [ ] двох її проекцій;

c) [ ] трьох її проекцій.

d) [ ] двох паралельних проекцій.

193. Прямі, які перпендикулярні до однієї із площин проекцій, а до двох інших розташовані паралельно називають прямими:

а) [ ] загального положення;

b) [ ] проекціювальними;

c) [ ] окремого положення;

d) [ ] рівня.

194. Прямі, які розташовані до однієї із площин проекцій, а до двох інших нахилені під кутом, називають прямими:

а) [ ] загального положення;

b) [ ] проекціювальними;

c) [ ] окремого положення;

d) [ ] рівня.

195. Пряма, паралельна горизонтальній площині проекцій, називається:

а) [ ] горизонтальною прямою;

b) [ ] фронтальною прямою;

c) [ ] горизонтально проекціювальною прямою;

d) [ ] прямою рівня.

196. Пряма, паралельна фронтальній площині проекцій, називається:

а) [ ] горизонтальною прямою;

b) [ ] фронтальною прямою;

c) [ ] фронтально проекціювальною прямою;

d) [ ] прямою рівня.

197. Пряма, паралельна профільній площині проекцій, називається:

а) [ ] профільною прямою;

b) [ ] фронтальною прямою;

c) [ ] профільно проекціювальною прямою;

d) [ ] прямою рівня.

198. Слідами прямої називають:

а) [ ] точки, через які проходить пряма;

b) [ ] точки перетину з осями координат;

c) [ ] точки перетину проекції з віссю ОХ;

d) [ ] точки перетину з основними площинами проекції.

199. Скільки слідів має пряма h:

а) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] 4.

200. Якщо дві прямі в просторі перетинаються, то:

а) [ ] їх однойменні проекції перетинаються;

b) [ ] їх однойменні проекції паралельні;

c) [ ] їх однойменні проекції перетинаються і точки перетину проекції знаходяться в проецюючому зв’язку;

d) [ ] їх однойменні проекції перетинаються в конкуруючих точках.

201. Якщо дві прямі в просторі паралельні, то:

а) [ ] їх однойменні проекції перетинаються;

b) [ ] їх однойменні проекції паралельні;

c) [ ] їх однойменні проекції перетинаються і точки перетину проекції знаходяться в проецюючому зв’язку;

d) [ ] їх однойменні проекції перетинаються в конкуруючих точках.

202. Якщо дві прямі в просторі мимобіжні, то:

а) [ ] їх однойменні проекції перетинаються

b) [ ] їх однойменні проекції паралельні

c) [ ] їх однойменні проекції перетинаються і точки перетину проекції знаходяться в проецюючому зв’язку.

d) [ ] їх однойменні проекції перетинаються в конкуруючих точках.

203. На яких рисунках прямі перетинаються:

а) [ ] b) [ ] c) [ ] d) [ ]

204. На яких рисунках прямі паралельні:

а) [ ] b) [ ] c) [ ] d) [ ]

205. На якому рисунку прямі мимобіжні:

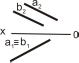
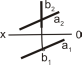
а) [ ] b) [ ] c) [ ] d) [ ]

206. На якому рисунку точка належить прямій?

a) [ ] а);

b) [ ] б), в), г);

c) [ ] а), г);

d) [ ] г).

207. На якому рисунку точка розміщується вище прямої?

a) [ ] б), в), г);

b) [ ] б);

c) [ ] в);

d) [ ] г).

208. На якому рисунку точка розміщується за прямою?

a) [ ] а);

b) [ ] б);

c) [ ] в);

d) [ ] г).

209. На якому рисунку точка розміщується попереду прямої?

a) [ ] а), г);

b) [ ] б);

c) [ ] в);

d) [ ] д).

210. На якому рисунку прямі у просторі мимобіжні?

a) [ ] а); b) [ ] б); c) [ ] в); d) [ ] г, д).

211. На якому рисунку прямі у просторі перетинаються?

a) [ ] а); b) [ ] б, г); c) [ ] в); d) [ ] а, д).

212. На якому рисунку прямі у просторі паралельні?

a) [ ] а); b) [ ] г); c) [ ] б, г); d) [ ] г, д).

213. Розташування площини в просторі визначають:

а) [ ] дві точки, через які проходить площина;

b) [ ] дві прямі, які перетинаються;

с) [ ] дві паралельні прямі;

d) [ ] дві мимобіжні прямі.

214. На якому рисунку зображено площину, яка задана паралельними прямими?

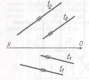
а) [ ] b) [ ] c) [ ] d) [ ]

215. На якому рисунку зображено площину, яка задана двома перехресними прямими?

а) [ ] b) [ ] c) [ ] d) [ ]

216. На якому рисунку площина задана двома перехресними прямими?

а) [ ] b) [ ] c) [ ] d) [ ]

217. Скільки граней має дана деталь?

а) [ ] 10; b) [ ] 11; c) [ ] 12; d) [ ] 13.

218. Як розташовані площини загального положення відносно основних площини проекції:

а) [ ] перпендикулярно до однієї з основних площин проекції;

b) [ ] паралельно до однієї з основних площин проекції;

с) [ ] не перпендикулярно до жодної з основних площин проекції;

d) [ ] паралельно до напрямку проеціювання.

219. Як називається площина перпендикулярна до горизонтальної площини проекції:

а) [ ] горизонтальною;

b) [ ] фронтально-проецюючою;

с) [ ] фронтальною;

d) [ ] горизонтально-проецюючою.

220. Як називається площина перпендикулярна до фронтальної площини проекції:

а) [ ] горизонтальною;

b) [ ] фронтально-проецюючою;

с) [ ] фронтальною;

d) [ ] горизонтально-проецюючою.

221. Як називається площина перпендикулярна до профільної площини проекції:

а) [ ] горизонтальною;

b) [ ] фронтально-проецюючою;

с) [ ] фронтальною;

d) [ ] профільно-проецюючою.

222. Як називається площина перпендикулярна до фронтальної і профільної площин проекцій:

а) [ ] горизонтальною;

b) [ ] фронтально-проецюючою;

с) [ ] фронтальною;

d) [ ] горизонтально-проецюючою.

223. Як називається площина перпендикулярна до горизонтальної і профільної площин проекцій:

а) [ ] горизонтальною;

b) [ ] фронтально-проецюючою;

с) [ ] фронтальною;

d) [ ] горизонтально-проецюючою.

224. Як називається площина перпендикулярна до горизонтальної і фронтальної площин проекцій:

а) [ ] профільною;

b) [ ] фронтально-проецюючою;

с) [ ] фронтальною;

d) [ ] горизонтально-проецюючою.

225. Як називається площина паралельна до горизонтальної площини проекції:

а) [ ] горизонтальною;

b) [ ] фронтально-проецюючою;

с) [ ] фронтальною;

d) [ ] горизонтально-проецюючою.

226. Як називається площина паралельна до фронтальної площини проекції:

а) [ ] горизонтальною;

b) [ ] фронтально-проецюючою;

с) [ ] фронтальною;

d) [ ] горизонтально-проецюючою.

227. Як називається площина паралельна до профільної площини проекції:

а) [ ] профільною;

b) [ ] фронтально-проецюючою;

с) [ ] фронтальною;

d) [ ] горизонтально-проецюючою.

228. Лінією скочування називають пряму:

а) [ ] паралельну до горизонталей в площині;

b) [ ] перпендикулярну до горизонталей в площині;

с) [ ] паралельну до фронталей в площині;

d) [ ] перпендикулярну до фронталей в площині.

229. На якому рисунку пряма належить площині?

a) [ ] а);

b) [ ] а), в), г), д);

c) [ ] б);

d) [ ] д).

230. На якому рисунку пряма не належить площині?

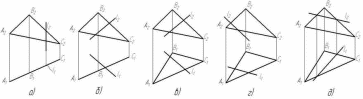
a) [ ] а), г), д);

b) [ ] а), в), г), д);

c) [ ] б), в), г), д);

d) [ ] д).

231. На якому рисунку пряма перетинає площину?

a) [ ] в);

b) [ ] б);

c) [ ] а), б);

d) [ ] б), в).

232. На якому рисунку пряма паралельна до площини?

a) [ ] а);

b) [ ] б), в);

c) [ ] г);

d) [ ] д).

233. На якому рисунку площини взаємнопаралельні?

a) [ ] а) b) [ ] б) c) [ ] а), б) d) [ ] на жодному

234. Лінія 1,2 - це лінія перетину двох площин, заданих трикутними відсіками ABC та DEF.

a) [ ] а);

b) [ ] б);

c) [ ] в);

d) [ ] а), б).

235. Яка точка належить площині?

a) [ ] 1, 2; b) [ ] 2; c) [ ] D; d) [ ] 1, D.

236. На яких кресленнях пряма l перпендикулярна до площини?

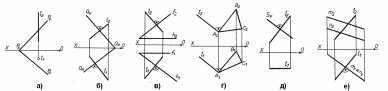
a) [ ] а), д);

b) [ ] б), в), д);

c) [ ] г), е);

d) [ ] а), б), в), д).

237. На яких кресленнях задані площини взаємноперпендикулярні?

a) [ ] а);

b) [ ] в), г), д);

c) [ ] д);

d) [ ] в), д).

238. Визначити розташування площини ∆ відносно основних площин проекцій:

а) [ ] горизонтальна; b) [ ] профільно-проецююча; с) [ ] загального положення; d) [ ] горизонтально-проецююча.

239. Визначити розташування площини ∆ відносно основних площин проекцій:

а) [ ] горизонтальна; b) [ ] профільно-проецююча; с) [ ] загального положення; d) [ ] горизонтально-проецююча.

240. Визначити розташування площини ∆ відносно основних площин проекцій:

а) [ ] горизонтальна; b) [ ] профільно-проецююча; с) [ ] загального положення; d) [ ] горизонтально-проецююча.

241. Визначити розташування площини ∆ відносно основних площин проекцій:

а) [ ] горизонтальна; b) [ ] фронтально-проецююча; с) [ ] загального положення; d) [ ] горизонтально-проецююча.

242. Визначити розташування площини ∆ відносно основних площин проекцій:

а) [ ] горизонтальна; b) [ ] фронтальна; с) [ ] загального положення; d) [ ] горизонтально-проецююча.

243. Визначити розташування площини ∆ відносно основних площин проекцій:

а) [ ] горизонтальна; b) [ ] фронтальна; с) [ ] загального положення; d) [ ] фронтально-проецююча.

244. Визначити розташування площини ∆ відносно основних площин проекцій:

а) [ ] горизонтальна; b) [ ] профільна; с) [ ] загального положення; d) [ ] горизонтально-проецююча.

245. На якому рисунку задана горизонтально-проекціювальна площина:

а) [ ] b) [ ] c) [ ] d) [ ]

246. На якому рисунку задана фронтально-проекціювальна площина?

а) [ ] b) [ ] c) [ ] d) [ ]

247. Пряма належить площині, якщо:

а) [ ] проходить через точку площини;

b) [ ] проходить через дві точки площини;

c) [ ] проходить через точку площини і паралельна прямій, яка лежить в цій площині;

d) [ ] паралельна прямій, яка лежить в площині.

248. Пряма паралельна площині, якщо:

а) [ ] проходить через точку площини;

b) [ ] дві точки площини;

c) [ ] проходить через точку площини і паралельна прямій, яка лежить в цій площині;

d) [ ] паралельна прямій, яка лежить в площині.

249. Пряма перпендикулярна площині, якщо:

а) [ ] перпендикулярна до прямої, яка лежить в площині;

b) [ ] перпендикулярна до горизонтальної площини;

c) [ ] перпендикулярна до двох прямих, які перетинаються в площині;

d) [ ] перпендикулярна до двох паралельних прямих в площині.

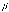250. Площина паралельна площині, якщо:

а) [ ] паралельна прямій, яка лежить в площині ;

b) [ ] проходить через перпендикуляр до площини ;

c) [ ] перпендикулярна до двох прямих, які перетинаються в площині ;

d) [ ] дві прямі які перетинаються в площині , паралельні двом прямим, які перетинаються в площині.

251. Площина перпендикулярна площині, якщо:

а) [ ] паралельна прямій, яка лежить в площині ;

b) [ ] проходить через перпендикуляр до площини ;

c) [ ] перпендикулярна до двох прямих, які перетинаються в площині ;

d) [ ] дві прямі які перетинаються в площині , паралельні двом прямим, які перетинаються в площині.

252. Чому дорівнюють координати точки зустрічі прямої l з площиною Р (f∩h):?

а) [ ] (); b) [ ] (); c) [ ] (); d) [ ] ().

253. Визначити відстань від точки А до площини ΔВСD:

а) [ ] ; b) [ ] ; c) [ ] ; d) [ ] .

254. Визначити відстань від точки А до площини Р (f ∩ h):

а) [ ] ; b) [ ] ; c) [ ] ; d) [ ] .

255. Визначити відстань від точки А до площини Р (f⁰ ∩ h⁰):

а) [ ] ; b) [ ] ; c) [ ] ; d) [ ] .

256. Визначите взаємне розташування площин:

a) [ ] перетинаються; b) [ ] паралельні; c) [ ] перпендикулярні; d) [ ] мимобіжні.

257. Визначите взаємне розташування площин:

a) [ ] перетинаються; b) [ ] паралельні; c) [ ] перпендикулярні; d) [ ] мимобіжні.

258. Визначити взаємне розташування прямої l і площини :

a) [ ] l належить ; b) [ ] l паралельна ; c) [ ] l перпендикулярна ; d) [ ] l перетинає .

259. Визначити взаємне розташування прямої l і площини :

a) [ ] l належить ; b) [ ] l паралельна ; c) [ ] l перпендикулярна ; d) [ ] l перетинає .

260. Визначити взаємне розташування прямої l і площини :

a) [ ] l належить ; b) [ ] l паралельна ; c) [ ] l перпендикулярна ; d) [ ] l перетинає .

261. Визначити взаємне розташування прямої l і площини :

a) [ ] l належить ; b) [ ] l паралельна ; c) [ ] l перпендикулярна ; d) [ ] l перетинає .

262. Основна позиційна задача - це:

a) [ ] задача на побудову точки перетину прямої і площини;

b) [ ] спосіб перетворення епюра;

c) [ ] задача на побудову лінії перетину двох площин;

d) [ ] задача на побудову перпендикуляра до площини.

263. Двогранний кут утворюється:

a) [ ] двома паралельними прямими;

b) [ ] двома площинами, які перетинаються;

c) [ ] двома прямими, які перетинаються;

d) [ ] двома паралельними площинами.

264. Мета перетворення комплексного креслення:

a) [  ] змінити розташування площин проекцій в просторі відносно геометричної фігури;

b) [  ] змінити взаємне розташування геометричної фігури і площин проекцій;

c) [  ] змінити напрям проеціювання;

d) [  ] змінити розташування геометричної фігури в просторі відносно площин проекцій.

265. Способом заміни площин проекцій можна будь-яку пряму загального положення перевести:

a) [ ] однією заміною в положення рівня;

b) [ ] однією заміною в проецююче положення;

c) [ ] двома замінами в положення рівня;

d) [ ] двома замінами в проецююче положення.

266. Способом заміни площин проекцій можна будь-яку площину загального положення перевести:

a) [ ] однією заміною в положення рівня;

b) [ ] однією заміною в проецююче положення;

c) [ ] двома замінами в положення рівня;

d) [ ] двома замінами в проецююче положення.

267. Способом плоскопаралельного переміщення можна будь-яку пряму загального положення перемістити:

a) [ ] одним переміщенням в положення рівня;

b) [ ] одним переміщенням в проецююче положення;

c) [ ] двома переміщеннями в положення рівня;

d) [ ] двома переміщеннями в проецююче положення.

268. Способом плоскопаралельного переміщення можна будь-яку площину загального положення перемістити:

a) [ ] одним переміщенням в положення рівня;

b) [ ] одним переміщенням в проецююче положення;

c) [ ] двома переміщеннями в положення рівня;

d) [ ] двома переміщеннями в проецююче положення.

269. Способом обертання навколо проецюючої прямої можна будь-яку пряму загального положення перемістити:

a) [ ] одним обертом в положення рівня;

b) [ ] одним обертом в проецююче положення;

c) [ ] двома обертами в проецююче положення;

d) [ ] двома обертами в положення рівня.

270. Способом обертання навколо проецюючої прямої можна будь-яку площину загального положення перемістити:

a) [ ] одним обертом в положення рівня;

b) [ ] одним обертом в проецююче положення;

c) [ ] двома обертами в проецююче положення;

d) [ ] двома обертами в положення рівня.

271. Спосіб суміщення це:

a) [ ] спосіб обертання навколо прямої рівня;

b) [ ] спосіб обертання навколо слідів площини;

c) [ ] спосіб обертання навколо проецюючої прямої;

d) [ ] спосіб заміни площин проекцій.

272. Скільки потрібно ввести допоміжних площин в систему П₁/П₂, щоб задана пряма загального положення була перпендикулярна до допоміжної площини проекцій?

a) [ ] одну;

b) [ ] дві;

c) [ ] три;

d) [ ] чотири.

273. Скільки потрібно ввести допоміжних площин в систему П₁/П₂, щоб отримати справжню величину відсіку площини загального положення?

a) [ ] одну;

b) [ ] дві;

c) [ ] три;

d) [ ] чотири.

274. На якому з рисунків допущена помилка при визначенні справжньої величини відрізка АВ?

a) [ ] а);

b) [ ] б);

c) [ ] в);

d) [ ] а), в).

275. На якому з рисунків досить однієї заміни площин проекцій для визначення справжньої величини трикутника АВС?

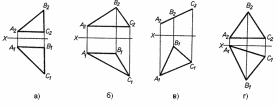
a) [ ] а);

b) [ ] б);

c) [ ] в);

d) [ ] г).

276. Перпендикулярно до якої прямої необхідно розташувати нову площину проекцій, щоб задана площина трикутника АВС була в новій системі проекцюючою?

a) [ ] AB; b) [ ] BC; c) [ ] AC; d) [ ] AD.

277. Як необхідно ввести нову площину проекцій, щоб відсік площини загального положення привести в проекцююче положення?

a) [ ] паралельно заданій площині;

b) [ ] перпендикулярно заданій площині;

c) [ ] під кутом;

d) [ ] довільно.

278. Як необхідно ввести нову площину проекцій, щоб пряма загального положення стала в новій системі лінією рівня?

a) [ ] паралельно заданій площині;

b) [ ] перпендикулярно заданій площині;

c) [ ] під кутом;

d) [ ] довільно.

279. Перпендикулярно до якої прямої необхідно розташувати нову площину проекцій, щоб знайти кут нахилу площини трикутника АВС до П₂?

a) [ ] AB; b) [ ] BC; c) [ ] AC; d) [ ] AD.

280. Яку необхідно вибрати вісь обертання, щоб відрізок прямої загального положення перевести в загальне положення?

a) [ ] горизонтально-проекцюючу;

b) [ ] фронтально-проекцюючу;

c) [ ] профільно-проекцюючу;

d) [ ] профільну.

282. Яку необхідно вибрати вісь обертання, щоб знайти кут нахилу відрізка прямої загального положення до П₁?

a) [ ] горизонтально-проекцюючу;

b) [ ] фронтально-проекцюючу;

c) [ ] профільно-проекцюючу;

d) [ ] горизонтальну.

283. Яку необхідно вибрати вісь обертання, щоб відсік площини загального положення перевести в горизонтально-проекююче положення?

a) [ ] горизонтально-проекцюючу;

b) [ ] фронтально-проекцюючу;

c) [ ] профільно-проекцюючу;

d) [ ] вертикальну.

284. Положення скількох точок трикутника загального положення необхідно побудувати, визначаючи натуральну величину відрізків, при обертанні його навколо лінії рівня до горизонтального положення?

a) [ ] однієї;

b) [ ] двох;

c) [ ] трьох;

d) [ ] чотирьох.

285. На якому з рисунків допущена помилка під час визначення справжньої величини відрізка АВ (А₁В₁, А₂В₂) обертанням його навколо прецюючоїї осі l(l₁,l₂)?

a) [ ] а);

b) [ ] б);

c) [ ] в);

d) [ ] а), в).

286. Яку пряму необхідно перевести в проекцююче положення, щоб площина трикутника АВС стала фронтально-проекцюючою?

a) [ ] AB;

b) [ ] BC;

c) [ ] AC;

d) [ ] CD.

287. Скільки разів необхідно повернути два відрізки паралельних прямих загального положення навколо проекцюючих осей, щоб визначити відстань між ними?

a) [ ] один раз;

b) [ ] два рази;

c) [ ] три рази;

d) [ ] чотири рази.

288. Положення скількох точок чотирикутника необхідно побудувати, визначаючи натуральну величину відрізків при обертанні його навколо лінії рівня до фронтального положення?

a) [ ] однієї;

b) [ ] двох;

c) [ ] трьох;

d) [ ] чотирьох.

289. Чи можна вважати плоскопаралельне переміщення обертанням навколо невизначених осей?

a) [ ] так;

b) [ ] ні;

c) [ ] не завжди;

d) [ ] частково.

290. На якому з рисунків допущена помилка при визначенні справжньої величини відрізка АВ?

a) [ ] а);

b) [ ] б);

c) [ ] в);

d) [ ] а, б.

291. Яким переміщенням необхідно вирішувати задачу на визначення відстані між мимобіжними прямими, якщо одна з них фронтальна?

a) [ ] фронтальним;

b) [ ] горизонтальним;

c) [ ] профільним;

d) [ ] горизонтально-проекцюючим.

292. На якому з рисунків помилково побудоване суміщене з горизонтальною площиною проекцій положення площини Р?

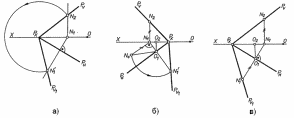
a) [ ] а);

b) [ ] б);

c) [ ] в);

d) [ ] б), в).

293. На якому кресленні, після вказаного перетворення, можна отримати дійсну величину двогранного кута при ребрі АВ:

1) 2) 3)

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] жодного.

294. Вказати номера рисунків (рис.1-3), якими позначено переміщення, що необхідні для розв’язку задачі: визначити дійсну величину відстані між мимобіжними прямими АВ і СD:

1) Умова 2) 3)

a) [ ] 1 і 2; b) [ ] 1 і 3; c) [ ] 2 і 3; d) [ ] 2 і 1.

295. Вказати номера рисунків (рис.1-3), якими позначено переміщення, що необхідні для розв’язку задачі: визначити дійсну величину відстані від точки А до прямої ВС:

1) Умова 2) 3)

a) [ ] 1 і 2; b) [ ] 1 і 3; c) [ ] 2 і 3; d) [ ] 2 і 1.

296. Вказати номера рисунків (рис.2-4), якими позначено переміщення, що необхідні для розв’язку задачі: визначити дійсну величину найкоротшої відстані між прямими, що перетинаються АВ і DC:

1) Умова 2) 3)

a) [ ] 1 і 2; b) [ ] 1; c) [ ] 2 ; d) [ ] 2 і 1.

297. Вказати номера рисунків (рис.1-3), якими позначено переміщення, що необхідні для розв’язку задачі: визначити дійсну величину відстані від точки А до прямої ВС:

1) Умова 2) 3)

a) [ ] 1 і 2; b) [ ] 1 і 3; c) [ ] 2 і 3; d) [ ] 2 і 1.

298. Вказати номера рисунків (рис.1-3), якими позначено переміщення, що необхідні для розв’язку задачі: визначити дійсну величину відстані між двома паралельними прямими:

1) Умова 2) 3)

a) [ ] 1 і 2; b) [ ] 1 і 3; c) [ ] 2 і 3; d) [ ] 2 і 1.

299. Вказати номера рисунків (рис.1-3), якими позначено переміщення, що необхідні для розв’язку задачі: визначити дійсну величину відстані від точки К до прямої CD:

1) Умова 2) 3)

a) [ ] 1 і 2; b) [ ] 1 і 3; c) [ ] 2 і 3; d) [ ] 2 і 1.

230. Вказати креслення на якому (рис.1-3) після вказаного перетворення можна визначити дійсну величину відстані від точки А до прямої ВС:

1) 2) 3)

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] жодного.

231. Вказати креслення на якому (рис.1-3) після вказаного перетворення можна визначити кут нахилу α площини ∑(fxh) до площини проекцій П1?

1) 2) 3)

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] жодного.

232. Вказати креслення на якому (рис.2-4) після вказаного перетворення можна отримати дійсну величину відстані від точки А до прямої ВС:

1) 2) 3)

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] жодного.

233. Вказати креслення (рис.1-3) на якому після вказаного перетворення можна отримати дійсну величину відстані між паралельними прямими АВ та CD:

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] жодного.

1) 2) 3)

234. На якому кресленні (рис.1-3) після вказаного перетворення можна отримати дійсну величину відстані між прямими АВ та CD, що перехрещуються після вказаного перетворення?

1) 2) 3)

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] жодного.

235. Відрізок, що вимірює відстань від точки до площини, проекціюється в натуральну величину на фронтальній площині проекцій, якщо площина займає:

а) [ ] горизонтально-проекціювальне положення;

b) [ ] фронтально-проекціювальне положення;

c) [ ] загальне положення;

d) [ ] окреме положення.

236. На якому кресленні (рис.1-3) після вказаного перетворення дана площина стане проекціювальною?

1) 2) 3)

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] жодного.

237. Відрізок, що вимірює відстань між паралельними площинами, проекціюється в натуральну величину на поле П₂, якщо площини займають:

а) [ ] горизонтально-проекціювальне положення;

b) [ ] фронтально-проекціювальне положення;

c) [ ] загальне положення;

d) [ ] окреме положення.

238. Відрізок, що вимірює відстань між паралельними площинами, проекціюється в натуральну величину на поле П₁, якщо площини займають:

а) [ ] проекціювальне положення;

b) [ ] горизонтально-проекціювальне положення;

c) [ ] фронтально-проекціювальне положення;

d) [ ] перпендикулярне положення.

239. Кут між двома площинами (двогранний кут) проекціюється в натуральну величину на поле П₁, якщо площини займають:

а) [ ] горизонтально-проекціювальне положення;

b) [ ] фронтально-проекціювальне положення;

c) [ ] загальне положення;

d) [ ] окреме положення.

240. Кут між двома площинами (двогранний кут) проекціюється в натуральну величину на поле П₂, якщо площини займають:

а) [ ] горизонтально-проекціювальне положення;

b) [ ] фронтально-проекціювальне положення;

c) [ ] загальне положення;

d) [ ] окреме положення.

241. Плоский кут утворюється:

a) [ ] двома паралельними прямими;

b) [ ] двома паралельними площинами;

c) [ ] двома прямими, які перетинаються;

d) [ ] двома площинами, які перетинаються.

242. Лінією перерізу многогранника площиною є:

a) [ ] плоска крива лінія;

b) [ ] просторова замкнута ламана лінія;

c) [ ] просторова крива лінія;

d) [ ] плоска замкнута ламана лінія.

243. Лінією перерізу кривої поверхні площиною є:

a) [ ] плоска замкнута крива лінія;

b) [ ] просторова замкнута ламана лінія;

c) [ ] просторова крива лінія;

d) [ ] плоска замкнута ламана лінія.

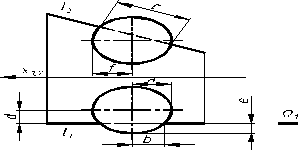
244. Для побудови точок перетину прямої l з циліндром доцільно скористатися

a) [ ] косокутним паралельним проекціюванням на П₁ за напрямком Ω;

b) [ ] косокутним паралельним проекціюванням на П₂ за напрямком Ω;

c) [ ] допоміжною січною площиною β;

d) [ ] допоміжною січною площиною Δ.

245. Для побудови точок перетину прямої l з конусом доцільно скористатися:

a) [ ] центральним проекціюванням на П₂ з центром S;

b) [ ] центральним проекціюванням на П₁ з центром S

c) [ ] допоміжною січною площиною Δ;

d) [ ] допоміжною січною площиною β.

246. Точками перетину прямої l з пірамідою будуть:

a) [ ] тільки точка A; b) [ ] тільки точка B; c) [ ] точки A та B; d) [ ] точки C та D.

247. Якщо перетнути конус допоміжною січною площиною Ω, що проходить через пряму l , то утвориться коло з радіусом що дорівнює розміру:

a) [ ] a; b) [ ] b; c) [ ] c; d) [ ] d.

248. Який спосіб доцільно вибрати для знаходження точок перетину прямої з похилим циліндром:

a) [ ] заміни площин проекцій;

b) [ ] центрального проекціювання;

c) [ ] паралельного косокутнього проекціювання;

d) [ ] плоскопаралельного перенесення.

249. Точками перетину прямої l із пірамідою будуть

a) [ ] тільки точка A; b) [ ] тільки точка B; c) [ ] тільки точка C; d) [ ] точки A та B.

250. Точками перетину прямої l з циліндром будуть

a) [ ] тільки точка A; b) [ ] тільки точка B; c) [ ] точки A та B; d) [ ] точки C та D.

251. Точками перетину прямої l із сферою будуть

a) [ ] тільки точка A; b) [ ] тільки точка B; c) [ ] точки A та B; d) [ ] точки C та D.

252. Якого положення слід вибирати площину – посередник в загальному випадку?

a) [ ] окремого положення;

b) [ ] тільки горизонтально-проекціюючу;

c) [ ] загального положення;

d) [ ] тільки фронтально-проекціюючу.

253. Щоб побудувати точки перетину прямої l із сферою доцільно скористатися допоміжною січною площиною:

a) [ ] Ω; b) [ ] γ; c) [ ] β; d) [ ] Δ.

254. Який спосіб доцільно вибрати для знаходження точок перетину прямої з похилою пірамідою:

a) [ ] заміни площин проекцій;

b) [ ] центрального проекціювання;

c) [ ] плоскопаралельного перенесення;

d) [ ] паралельного косокутнього проекціювання.

255. Коли можуть дві точки перетину прямою багатогранника бути розміщеними на одній і тій же грані?

a) [ ] коли бічні грані а загальному положенні;

b) [ ] коли бічні грані в окремому положенні;;

c) [ ] коли багатогранник правильний;

d) [ ] коли багатогранник неправильний.

256. Використання способу посередників доцільне у випадку знаходження:

a) [ ] перетину прямої та площини з поверхнею;

b) [ ] натуральної величин довжини ребер многогранника;

c) [ ] побудови прямої, що паралельна до заданої;

d) [ ] побудови слідів площини.

257. Як визначити видимість окремих частин прямої при її перетині з поверхнею на комплексному кресленні?

a) [ ] методом заміни площин проекцій;

b) [ ] методом конкуруючих точок;

c) [ ] методом обертання;

d) [ ] методом плоскопаралельного перенесення.

258. Який спосіб доцільно вибрати для знаходження точок перетину прямої з похилою призмою:

a) [ ] заміни площин проекцій;

b) [ ] плоскопаралельного перенесення;

c) [ ] обертання;

d) [ ] паралельного косокутнього проекціювання.

259. Який спосіб доцільно вибрати для знаходження точок перетину прямої із сферою:

a) [ ] заміни площин проекцій;

b) [ ] центрального проекціювання;

c) [ ] плоскопаралельного перенесення;

d) [ ] паралельного косокутнього проекціювання.

260. Коли може бути відсутнім перетин площини і піраміди?

a) [ ] коли дана площина паралельна одній з бічних граней;

b) [ ] коли піраміда правильна;

c) [ ] коли піраміда неправильна;

d) [ ] коли бічні грані в окремому положенні.

261. Який спосіб доцільно вибрати для знаходження точок перетину прямої з похилим конусом:

a) [ ] заміни площин проекцій;

b) [ ] центрального проекціювання;

c) [ ] паралельного косокутнього проекціювання;

d) [ ] плоскопаралельного перенесення.

262. Якщо перетнути сферу допоміжною січною площиною Ω, що проходить через пряму l , то утвориться коло з радіусом що дорівнює розміру:

a) [ ] a b) [ ] b c) [ ] c d) [ ] d

263. Визначити на якому кресленні зображено точку перетину горизонтально-проектуючої прямою з конічною поверхнею обертання:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

264. Визначити на якому кресленні зображено точку перетину профільно-проектуючої прямою з конічною поверхнею обертання:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] в), б)

265. Визначити на якому кресленні зображено точку перетину фронтально-проектуючої прямою з конічною поверхнею обертання:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), в)

266. Визначити на якому кресленні зображено точку перетину горизонтальної лінії рівня з конічною поверхнею обертання:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

267. Визначити на якому кресленні зображено точку перетину фронтальної лінії рівня з конічною поверхнею обертання:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

268. Визначити на якому кресленні зображено точку перетину фронтальної лінії рівня з конічною поверхнею обертання:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

269. Визначити на якому кресленні зображено точку перетину горизонтальної лінії рівня з конічною поверхнею обертання:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

270. Визначити на якому кресленні зображено точку перетину горизонтальної лінії рівня з циліндричною поверхнею:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

271. Визначити на якому кресленні зображено точки перетину фронтальної лінії рівня з циліндричною поверхнею:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

272. Визначити на якому кресленні зображено точку перетину профільно-проектуючої прямої з циліндричною поверхнею:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

273. Визначити на якому кресленні зображено точки перетину фронтально-проектуючої прямої з циліндричною поверхнею:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

274. Визначити на якому кресленні зображено точки перетину прямої загального положення з циліндричною поверхнею:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

275. Визначити на якому кресленні зображено точки перетину прямої загального положення з циліндричною поверхнею:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

276. Визначити на якому кресленні зображено точки перетину прямої з циліндричною поверхнею:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

277. Визначити на якому кресленні зображено точки перетину прямої із сферою:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

278. Визначити на якому кресленні зображено точки перетину прямої із сферою:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

279. Визначити на якому кресленні зображено точки перетину прямої із сферою:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

280. Визначити на якому кресленні зображено точки перетину прямої із сферою:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

281. Визначити на якому кресленні зображено точки перетину прямої із сферою:

a) [ ] а) b) [ ] б) c) [ ] в) d) [ ] а), б)

282. Коли точка належить поверхні?

a) [ ] коли точка належить лінії, що належить цій поверхні;

b) [ ] коли точка належить прямій, що належить цій поверхні;

c) [ ] коли точка належить двом перетинним прямим цієї поверхні;

d) [ ] коли точка належить прямій, що не належить цій поверхні.

283. Які точки не належать поверхні сфери?

a) [ ] A b) [ ] B c) [ ] C d) [ ] A, B

284. Які точки не належать поверхні конуса?

a) [ ] A; b) [ ] B, С; c) [ ] C; d) [ ] D.

285. Які точки належать заданій кривій поверхні?

a) [ ] A; b) [ ] B; c) [ ] C; d) [ ] A, B.

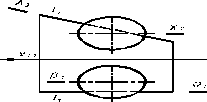
286. Лінія перетину гіперболічного параболоїда площиною паралельною П₂ називаються:

a) [ ] еліпсом; b) [ ] параболою; c) [ ] гіперболою; d) [ ] випадковою кривою.

287. Лінія перетину гіперболічного параболоїда площиною паралельною П₃ називаються:

a) [ ] еліпсом; b) [ ] параболою; c) [ ] гіперболою; d) [ ] випадковою кривою.

288. Еліпс утворюється в результаті перетину прямого кругового конуса обертання площиною:

a) [ ] ; b) [ ] ; c) [ ] ; d) [ ] λ.

289. Коло утворюється в результаті перетину прямого кругового конуса обертання площиною:

a) [ ] ; b) [ ] ; c) [ ] ; d) [ ] Ψ.

290. Гіпербола утворюється в результаті перетину прямого кругового конуса обертання площиною:

a) [ ] ; b) [ ] ; c) [ ] ; d) [ ] Ψ.

291. Парабола утворюється в результаті перетину прямого кругового конуса обертання площиною:

a) [ ] ; b) [ ] ; c) [ ] ; d) [ ] Ψ.

292. Трикутник утворюється в результаті перетину прямого кругового конуса обертання площиною:

a) [ ] ; b) [ ] ; c) [ ] ; d) [ ] λ.

293. Який переріз кулі відповідає положенню січної площини Q?

1) 2) 3)

a) [ ] 1 b) [ ] 2 c) [ ] 3 d) [ ] жодного.

294. Який переріз тора відповідає положенню січної площини R?

1) 2) 3)

a) [ ] 1;

b) [ ] 2;

c) [ ] 3;

d) [ ] жодного.

295. Яка площина перетинає конус обертання по гіперболі?

a) [ ] P b) [ ] Q c) [ ] S d) [ ] T

296. Чому дорівнює довжина розгортки бічної поверхні прямого циліндра обертання, якщо його радіус дорівнює?

a) [ ] R²

b) [ ] 2R

c) [ ] R²

d) [ ] 2R²

297. Яка з ліній, що належить поверхні конуса, зобразиться на розгортці прямою?

a) [ ] a b) [ ] b c) [ ] a, c d) [ ] b, c

298. Скільки дотичних площин можна провести через задану точку до циліндра, конуса, кулі?

a) [ ] 1;

b) [ ] 2;

c) [ ] 3;

d) [ ] безліч.

299. Як буде перетинати гіперболічний параболоїд дотична площина, проведена до цієї поверхні в заданій на ній точці?

a) [ ] по одній прямій;

b) [ ] по одній прямій і одній кривій;

c) [ ] по двох прямих;

d) [ ] по двох кривих.

300. Скільки можна провести дотичних площин до еліпсоїда обертання через зовнішню власну точку?

a) [ ] одну;

b) [ ] дві;

c) [ ] жодної;

d) [ ] безліч.

301. За яких умов можна провести площини, дотичну до конуса обертання і паралельну заданій площині?

a) [ ] якщо задана площина паралельна осі конуса;

b) [ ] якщо задана площина паралельна будь-якій твірній конуса;

c) [ ] якщо в заданій площині можна вибрати пряму, паралельну лише одній будь-якій твірній конуса;

d) [ ] якщо задана площина перпендикулярна осі конуса.

302. На якому рисунку зображено тетраедр:

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] 4.

303. На якому рисунку зображено куб?

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] 4.

304. На якому рисунку зображено піраміду?

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] 4.

305. На якому рисунку зображено додекаедр?

a) [ ] 1; b) [ ] 2; c) [ ] 3; d) [ ] 4.

306. На якому рисунку зображено ікосаедр?

a) [ ] 2; b) [ ] 3; c) [ ] 4; d) [ ] 5.

307. Скільки граней має тетраедр?

a) [ ] 4;

b) [ ] 6;

c) [ ] 8;

d) [ ] 12.

308. Скільки граней має куб?

a) [ ] 4;

b) [ ] 6;

c) [ ] 8;

d) [ ] 12.

309. Скільки граней має октаедр?

a) [ ] 4;

b) [ ] 6;

c) [ ] 8;

d) [ ] 12.

310. Скільки граней має додекаедр?

a) [ ] 4;

b) [ ] 6;

c) [ ] 20;

d) [ ] 12.

311. Скільки граней має ікосаедр?

a) [ ] 4;

b) [ ] 6;

c) [ ] 20;

d) [ ] 12.

312. Скільки ребер має тетраедр?

a) [ ] 6;

b) [ ] 20;

c) [ ] 30;

d) [ ] 12

313. Скільки ребер має куб?

a) [ ] 6;

b) [ ] 20;

c) [ ] 30;

d) [ ] 12.

314. Скільки ребер має октаедр?

a) [ ] 6;

b) [ ] 20;

c) [ ] 30;

d) [ ] 12.

315. Скільки ребер має додекаедр?

a) [ ] 6;

b) [ ] 20;

c) [ ] 30;

d) [ ] 12.

316. Скільки ребер має ікосаедр?

a) [ ] 6;

b) [ ] 20;

c) [ ] 30;

d) [ ] 12.

317. Яку форму граней має тетраедр

a) [ ] трикутник;

b) [ ] квадрат;

c) [ ] п'ятикутник;

d) [ ] шестикутник.

318. Яку форму граней має куб

a) [ ] трикутник;

b) [ ] квадрат;

c) [ ] п'ятикутник;

d) [ ] шестикутник.

319. Яку форму граней має октаедр

a) [ ] трикутник;

b) [ ] квадрат;

c) [ ] п'ятикутник;

d) [ ] шестикутник.

320. Яку форму граней має додекаедр

a) [ ] трикутник;

b) [ ] квадрат;

c) [ ] п'ятикутник;

d) [ ] шестикутник.

321. Яку форму граней має ікосаедр

a) [ ] трикутник;

b) [ ] квадрат;

c) [ ] п'ятикутник;

d) [ ] шестикутник.

322. Яку кількість вершин має тетраедр

a) [ ] 4;

b) [ ] 8;

c) [ ] 6;

d) [ ] 20.

323. Яку кількість вершин має куб

a) [ ] 4;

b) [ ] 8;

c) [ ] 6;

d) [ ] 20.

324. Яку кількість вершин має октаедр

a) [ ] 4;

b) [ ] 8;

c) [ ] 6;

d) [ ] 20.

325. Яку кількість вершин має додекаедр

a) [ ] 4;

b) [ ] 8;

c) [ ] 6;

d) [ ] 20.

326. Яку кількість вершин має ікосаедр

a) [ ] 4;

b) [ ]12;

c) [ ] 6;

d) [ ] 20.

327. Зі скількох плоских фігур складається повна розгортка правильної шестикутної призми?

a) [ ] 6;

b) [ ] 5;

c) [ ] 8;

d) [ ] 7.

328. Зі скількох плоских фігур складається повна розгортка правильної шестикутної піраміди?

a) [ ] 7;

b) [ ] 8;

c) [ ] 6;

d) [ ] 5.

329. Зі скількох плоских фігур складається повна розгортка правильної п’ятикутної призми?

a) [ ] 8;

b) [ ] 7;

c) [ ] 6;

d) [ ] 5.

330. Зі скількох плоских фігур складається повна розгортка правильної п’ятикутної піраміди?

a) [ ] 8;

b) [ ] 7;

c) [ ] 6;

d) [ ] 5.

331. Зі скількох плоских фігур складається повна розгортка правильної чотирикутної призми?

a) [ ] 7;

b) [ ] 6;

c) [ ] 5;

d) [ ] 4.

332. Зі скількох плоских фігур складається повна розгортка правильної чотирикутної піраміди?

a) [ ] 7;

b) [ ] 6;

c) [ ] 5;

d) [ ] 4.

333. Зі скількох плоских фігур складається повна розгортка правильної трикутної призми?

a) [ ] 6;

b) [ ] 5;

c) [ ] 4;

d) [ ] 3.

334. Зі скількох плоских фігур складається повна розгортка правильної трикутної піраміди?

a) [ ] 6;

b) [ ] 5;

c) [ ] 4;

d) [ ] 3.

335. Яким способом побудована розгортка многогранника, що зображений на рисунку?

a) [  ] спосіб нормального перерізу; b) [  ] спосіб розгортання; c) [  ] спосіб трикутників; d) [  ] спосіб прямокутного трикутника.

336. Яким способом побудована розгортка многогранника, що зображений на рисунку?

a) [ ] спосіб нормального перерізу; b) [ ] спосіб розгортання; c) [ ] спосіб трикутників; d) [ ] спосіб обертання.

337. Яким способом побудована розгортка многогранника, що зображений на рисунку?

a) [ ] спосіб нормального перерізу; b) [ ] спосіб розгортання; c) [ ] спосіб трикутників; d) [ ] спосіб обертання.

338. Яка розгортка зображена на рисунку?

a) [  ] повна розгортка п’ятикутної піраміди; b) [  ] розгортка бічної поверхні п’ятикутної піраміди; c) [  ] розгортка бічної поверхні зрізаної п’ятикутної піраміди; d) [  ] розгортка бічної поверхні зрізаної неправильної п’ятикутної піраміди.

339. Розгортка якого многогранника зображена на рисунку?

a) [ ] правильної чотирикутної піраміди; b) [ ] неправильної чотирикутної призми; c) [ ] похилої чотирикутної призми; d) [ ] прямокутного паралелепіпеда.

340. Розгортка якого многогранника зображена на рисунку?

a) [ ] правильної п’ятикутної піраміди; b) [ ] неправильної шестикутної піраміди; c) [ ] правильної шестикутної піраміди; d) [ ] неправильної шестикутної призми.

341. Розгортка якого многогранника зображена на рисунку?

a) [ ] правильної чотирикутної призми; b) [ ] неправильної чотирикутної призи; c) [ ] похилої чотирикутної призми; d) [ ] похилої п’ятикутної призми.

342. Розгортка якого многогранника зображена на рисунку?

a) [ ] правильної трикутної піраміди; b) [ ] неправильної трикутної піраміди; c) [ ] правильної чотирикутної піраміди; d) [ ] неправильної чотирикутної піраміди.

343. Яка розгортка зображена на рисунку?

a) [  ] повна розгортка неправильної трикутної призми b) [  ] повна розгортка правильної трикутної призми c) [  ] розгортка бічної поверхні правильної трикутної призми d) [  ] розгортка нижньої зрізаної частини правильної трикутної призми

344. Яка розгортка зображена на рисунку?

a) [ ] повна розгортка неправильної трикутної піраміди; b) [ ] повна розгортка правильної трикутної піраміди; c) [ ] повна розгортка правильної трикутної піраміди з нанесенням лінії перетину; d) [ ] неповна розгортка правильної трикутної піраміди

345. Лінія перетину поверхні розгорток гелікоїда з горизонтальною площиною називається:

a) [ ] гіперболою; b) [ ] еліпсом; c) [ ] параболою; d) [ ] евольвентою.

346. Яку форму має розгортка бічної поверхні прямого конуса обертання з основою, перпендикулярною до осі конуса?

a) [ ] сегмент;

b) [ ] сектор;

c) [ ] бічна поверхня;

d) [ ] коло.

347. Яким способом побудована розгортка циліндра?

a) [ ] нормального перерізу; b) [ ] розгортання; c) [ ] трикутників; d) [ ] обертання.

348. Яким способом побудована розгортка похилого циліндра?

a) [ ] нормального перерізу; b) [ ] розгортання; c) [ ] трикутників; d) [ ] обертання.

349. Яким способом побудована розгортка конуса?

a) [ ] нормального перерізу; b) [ ] розгортання; c) [ ] трикутників; d) [ ] обертання.

350. Яким способом побудована розгортка похилого конуса?

a) [ ] нормального перерізу; b) [ ] розгортання; c) [ ] трикутників; d) [ ] обертання.

351. Яким способом побудована розгортка поверхні циліндроїда?

a) [ ] нормального перерізу; b) [ ] розгортання; c) [ ] трикутників; d) [ ] обертання.

352. Лінією перерізу двох многогранників є:

a) [ ] плоска крива лінія;

b) [ ] просторова замкнута ламана лінія;

c) [ ] просторова крива лінія;

d) [ ] плоска замкнута ламана лінія.

353. Лінією перерізу двох кривих поверхонь є:

a) [ ] плоска крива лінія;

b) [ ] просторова замкнута ламана лінія;

c) [ ] просторова крива лінія;

d) [ ] плоска замкнута ламана лінія.

354. Що є лінією перетину циліндра і сфери, що зображені на рисунку:

a) [ ] два кола b) [ ] два еліпса c) [ ] крива 4-го порядку d) [ ] дві прямі

355. Що є лінією перетину конуса і сфери, що зображені на рисунку?

a) [ ] два кола b) [ ] два еліпса c) [ ] крива 4-го порядку d) [ ] дві прямі

356. Що є лінією перетину тора і сфери, що зображені на рисунку?

a) [ ] два кола b) [ ] два еліпса c) [ ] крива 4-го порядку d) [ ] дві прямі

357. Що є лінією перетину двох циліндрів, що зображені на рисунку?

a) [ ] два кола b) [ ] два еліпса c) [ ] крива 4-го порядку d) [ ] дві прямі

358. Що є лінією перетину двох циліндрів, що зображені на рисунку?

a) [ ] два кола b) [ ] два еліпса c) [ ] крива 4-го порядку d) [ ] дві прямі

359. Що є лінією перетину двох конусів, що зображені на рисунку?

a) [ ] два кола b) [ ] два еліпса c) [ ] крива 4-го порядку d) [ ] дві прямі

360. Що є лінією перетину конуса і циліндра, що зображені на рисунку?

a) [ ] два кола b) [ ] два еліпса c) [ ] крива 4-го порядку d) [ ] дві прямі

361. Що є лінією перетину двох конусів, що зображені на рисунку?

a) [ ] два кола b) [ ] два еліпса c) [ ] крива 4-го порядку d) [ ] дві прямі

362. Що є лінією перетину двох циліндрів, що зображені на рисунку?

a) [ ] два кола b) [ ] два еліпса c) [ ] крива 4-го порядку d) [ ] дві прямі

363. Що є лінією перетину двох циліндрів, що зображені на рисунку?

a) [ ] два кола b) [ ] два еліпса c) [ ] крива 4-го порядку d) [ ] дві прямі

364. Який метод треба використовувати для побудови лінії перетину циліндра і сфери, що зображені на рисунку ?

a) [  ] допоміжних січних площин; b) [  ] концентричних сфер; c) [  ] ексцентричних сфер; d) [  ] пучка площин, які проходять через власну пряму.

365. Який метод треба використовувати для побудови лінії перетину тора і конуса, що зображені на рисунку ?

a) [  ] допоміжних січних площин; b) [  ] концентричних сфер; c) [  ] ексцентричних сфер; d) [  ] пучка площин, які проходять через власну пряму.

366. Який метод треба використовувати для побудови лінії перетину двох похилих конусів, що зображені на рисунку ?

a) [  ] допоміжних січних площин; b) [  ] концентричних сфер; c) [  ] ексцентричних сфер; d) [  ] пучка площин, які проходять через власну пряму.

367. Який метод треба використовувати для побудови лінії перетину конуса і циліндра, що зображені на рисунку ?

a) [  ] допоміжних січних площин; b) [  ] концентричних сфер; c) [  ] ексцентричних сфер; d) [  ] пучка площин, які проходять через власну пряму.

368. Який метод треба використовувати для побудови лінії перетину тора і циліндра, що зображені на рисунку ?

a) [  ] допоміжних січних площин; b) [  ] концентричних сфер; c) [  ] ексцентричних сфер; d) [  ] пучка площин, які проходять через власну пряму.

369. Який метод треба використовувати для побудови лінії перетину двох конусів, що зображені на рисунку ?

a) [  ] допоміжних січних площин; b) [  ] концентричних сфер; c) [  ] ексцентричних сфер; d) [  ] пучка площин, які проходять через власну пряму.

370. Який метод треба використовувати для побудови лінії перетину двох похилих циліндрів, що зображені на рисунку ?

a) [  ] допоміжних січних площин; b) [  ] концентричних сфер; c) [  ] ексцентричних сфер; d) [  ] пучка площин, які проходять через власну пряму.

371. Який метод треба використовувати для побудови лінії перетину тора і циліндра, що зображені на рисунку ?

a) [  ] допоміжних січних площин; b) [  ] концентричних сфер; c) [  ] ексцентричних сфер; d) [  ] пучка площин, які проходять через власну пряму.

372. Який метод треба використовувати для побудови лінії перетину двох конусів, що зображені на рисунку ?

a) [  ] допоміжних січних площин; b) [  ] концентричних сфер; c) [  ] ексцентричних сфер; d) [  ] пучка площин, які проходять через власну пряму.

373. Який метод треба використовувати для побудови лінії перетину конуса і циліндра, що зображені на рисунку ?

a) [  ] допоміжних січних площин; b) [  ] концентричних сфер; c) [  ] ексцентричних сфер; d) [  ] пучка площин, які проходять через власну пряму.

374. Яким методом доцільно вирішувати задачу взаємного перетину многогранників, що зображені на рисунку?

a) [  ] методом прямокутного трикутника; b) [  ] методом січних сфер; c) [  ] методом січних площин; d) [  ] методом обертання.

375. Яким методом доцільно вирішувати задачу взаємного перетину многогранників, що зображені на рисунку?

a) [ ] методом обертання; b) [ ] методом заміни площин проекцій; c) [ ] методом косокутного проектування; d) [ ] методом січних сфер.

376. Яким методом доцільно вирішувати задачу взаємного перетину многогранників, що зображені на рисунку?

a) [ ] методом прямокутного трикутника; b) [ ] методом січних сфер; c) [ ] методом центрального допоміжного проектування; d) [ ] методом обертання.

377. На рисунку показані дві трикутні похилі призми, що перетинаються і побудовані їх косокутні проекції на площину основ. Яке з трьох тверджень вірне?

a) [  ] лінія взаємного перетину є просторовою замкненою ламаною, що має шість вершин; b) [  ] лінія взаємного перетину розпадається на дві лінії: ліню входу і лінію виходу; c) [  ] лінія взаємного перетину є просторовою замкненою ламаною, що має вісім вершин; d) [  ] лінія взаємного перетину є плоскою замкненою ламаною, що має шість вершин.

378. Чи всі бічні грані обох призм, що перетинаються приймають участь у перетині?

a) [ ] так; b) [ ] ні; c) [ ] 2 грані; d) [ ] 3 грані.

379. Скільки бічних ребер трикутної призми приймає участь у перетині?

a) [ ] одне; b) [ ] два; c) [ ] три; d) [ ] чотири.

Рекомендована література

Основна

• Антонович Э.А. Нарисна геометрія. Практикум: навч. посібник / Э.А. Антонович та ін. [За ред. проф. Є.А. Антоновича]. – Львів : Світ, 2004.

• Державні стандарти: ГОСТ 2.301-68 (СТ РЕВ 1181-78) – формати; ГОСТ 2.104-68 (СТ РЕВ 140-74, СТ РЕВ 365-76) – основні написи; ГОСТ 2.302-68 (СТ РЕВ 1180-78) – масштаби; ГОСТ 2.303-68 (СТ РЕВ 1178-78) – лінії; ГОСТ 2.304-81 (СТ РЕВ 851-78...СТ РЕВ 855-78) – шрифти креслярські.

• Курс нарисної геометрії. Навчальний посібник / О.М. Джеджула, С.І. Кормановський, А.В. Спірін, М.В. Пятак, А.Й. Островський. – Вінниця : ВНАУ, 2011. – 200 с.

• Михайленко В.Є. Нарисна геометрія / В.Є. Михайленко, М.Ф. Євстифєєв, С.М. Ковальов, О.В. Кащенко. – К. : Вища шк., 2004.

• Нарисна геометрія. Навчально-методичний посібник до організації самостійної роботи студентів / О.С. Магопець, Т.М. Ауліна. – Кіровоград: 2004. – 127с.: Рекомендовано Міністерством освіти і науки України як навчальний посібник для студентів вищих навчальних закладів (лист 14/18.2 – 2059 від 16.09.04).

• Юсупова М.Ф. Начертательная геометрия и АutoCAD: Учебное пособие для студентов высших учебных заведений. – Одесса : Друк, 2005. – 302 с.

Додаткова

• Бубенников А.В. Начертательная геометрия. Задачи для упражнений: Учеб. пособие / А.В. Бубенников. – М.: Высш. шк., 1981.

• Бубенников А.В. Начертательная геометрия: Уч. для втузов / А.В. Бубенников. – 3-е изд. – М. : Высш. шк., 1985.

• Винницкий И.Г. Начертательная геометрия. Уч. для вузов / И.Г. Винницкий. – М. : Высш. шк., 1975.

• Гордон В.Л. Сборник задач по курсу начертательной геометрии / В.Л. Гордон, Ю.П. Иванов, Т.Е. Солнцева. – М. : Наука, 1978.

• Гордон В.О. Курс начертательной геометрии / В.О. Гордон, М.А. Семенцов-Огиевский. – М.: Наука, 1987.

• Климухин А.Г. Сборник задач по начертательной геометрии: Учеб. пособие для вузов / А.Г. Климухин. – М. : Стройиздат, 1982.

• Крівцов В.В. Нарисна геометрія: Навч. посібник / В.В. Крівцов, С.С. Дєєв. – К. : НМВ ВО, 1992. – 244с.

• Начертательная геометрия. 3-е изд., переработанное / Н.Л. Русскевич. – К. : Вища шк., 1978.

• Сборник задач по начертательной геометрии / Х.А. Арустамов. – М. : Машиностроение, 1971.

• Сборник задач по начертательной геометрии в системе АutoCAD: Учебное пособие для студентов высших учебных заведений. – Одесса : Друк, 2004. – 252 с.

• Фольта О.В. Нарисна геометрія: Навчальне видання / О.В. Фольта, Є.А. Антонович. П.П. Юрковський. – Львів : Світ, 1994.

• Фролов С.А. Начертательная геометрия / С.А. Фролов. – М. : Машиностроение, 1978.

• Чекмарев А.А. Начертательная геометрия и черчение: Учеб. пособие для студентов пед. ин-тов по спец. №2120 „Общетехн. дисциплины и труд” / А.А. Чекмарев. – М. : Просвещение, 1987.

Інформаційні ресурси (перелік адрес інтернет-ресурсів з коротким описом)

20. http://dvoika.net/ (Сайт містить навчальний матеріал з нарисної геометрії та креслення)

21. http://www.chertilnik.ru/ingraf_teoriya.html (Сайт містить теоретичну інформацію з курсу НГК)

22. http://www.gubkin.ru/faculty/mechanical_engineering/chairs_and_departm s/automation_designing_buildings/questions-0506.php (Сайт містить довідкову інформацію по ГОСТ'ам для виконання креслень).

Навчальне видання

Гриценко Лариса Олександрівна
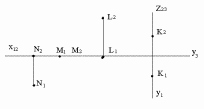
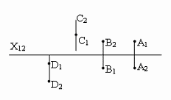
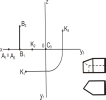
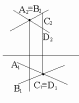