16. Симплексный метод лп: исследование данного базисного допустимого решения на оптимальность, условия оптимальности в случае минимизируемой и максимизируемой функции цели.

Из выражения L=L₀-∆_m+1x_m+1-...-∆_nx_n (1) следует, что базисное решение x₁=h₁, x₂=h₂,...x_m=h_m, x_m+1=0,...x_n=0 (2) является оптимальным решением задачи ЛП

L=c₁x₁+c₂x₂+...c_nx_n ,при условиях:

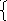x₁ + g_1,m+1x_m+1 + ... + g_1nx_n = h₁,

x₂ + g_2,m+1 x_m+1 + ... + g_2nx_n = h₂,

x_m + g_m,m+1 x_m+1 + ... + g_mnx_n = h_m

и x_j≥0, j = 1,2,...n, тогда и только тогда, когда в уравнении L=∆_m+1x_m+1+...+∆_nx_n=L₀ среди коэффициентов ∆_j при неизвестных нет ни одного положительного, т.е. условие оптимальности имеет вид: ∆_j ≤0, j=1,2,...n.

Действительно, если в общем решении x_i=h_i-g_i,m+1x_m+1-...-g_inx_n, i=1,2,...,m мы станем придавать различные неотрицательные значения свободным неизвестным так, чтобы соответствующие базисные неизв-е принимали неотрицательные значения, то одновременно с частными неотрицательными решениями с-мы ограничений будем получать согласно выражению (1), соответствующие им значения целевой ф-ии. В частности, при нулевых значениях свободных неизвестных получится базисное решение (2) и соответствующее ему значение линейной формы

L₀=c₁h₁+c₂h₂+...c_mh_m+c_m+1*0+...+c_n*0 = c_i h_i

17. Симплексный метод лп: условие единственности базисного оптимального решения. Условие неограниченности целевой ф-ии на множестве допустимых решений.

При выполнении условия оптимальности базисное решение x₁=h₁, x₂=h₂,...x_m=h_m, x_m+1=0,...x_n=0 будет единственным оптимальным решением задачи ЛП тогда, и только тогда, когда все коэффициенты ∆_m+1, ∆_m+2,…, ∆_n при свободных неизвестных в последнем уравнении вспомогательной системы

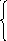x_i + g_ijx_j = h_i , i= 1,2,...m,

L + ∆_jx_j = L₀

Строго отрицательны. Если же хотя бы один из коэффициентов при свободных неизвестных равен нулю, то будут и небазисные оптимальные решения.

Если есть хотя бы одна свободная неизвестная, такая что коэффициент ∆_j при ней в последнем уравнении системы (1) положителен, а в первых m уравнениях той же системы среди коэффициентов g_1j, g_2j, …g_mj при ней нет ни одного положительного, то задача линейного прогрмаммирования неразрешима в силу неограниченности линейной формы L=c₁x₁+c₂x₂+...c_nx_nна множестве неотрицательных решений системы ограничений

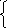x₁ + g_1,m+1x_m+1 + ... + g_1nx_n = h₁,

x₂ + g_2,m+1 x_m+1 + ... + g_2nx_n = h₂, (2)

... ... ... ...

x_m + g_m,m+1 x_m+1 + ... + g_mnx_n = h_m.

18. Симплексный метод ЛП: переход от одного базисного допустимого решения к другому. Правила выбора разрешающей неизвестной и разрешающего уравнения, их обоснование. Монотонность и конечность симплексного алгоритма для невырожденной задачи ЛП, понятие о зацикливании.

Предположим, что базисное решение не является оптимальным, т.е. среди коэффициентов ∆_j есть по меньшей мере один положительный. Проще всего проследить за поведением целевой функции тогда, когда изменяется только одна свободная неизвестная, а остальные свободные неизвестные сохраняют нулевые значения, которые они имели в базисном решении. Каждая свободная неизвестная при нулевых значениях других свободных неизвестных имеет свою неотрицательную область изменения, нижняя граница которой всегда равна нулю, а верхняя граница является конечной или бесконечной в зависимости от того, есть или нет при данной неизвестной в соответствующем предпочитаемом виде системы уравнений хотя бы один положительный коэффициент. Если есть хотя бы одна свободная неизвестная, коэффициент ∆_j при которой в последнем уравнении системы положителен, а в первых m уравнениях той же системы среди коэффициентов g_1j, g_2j,….,g_mj при ней нет ни одного положительного, то задача линейного программирования неразрешима в силу неограниченности линейной формы на множестве неотрицательных решений системы ограничений.

Допустим, что базисное решение не оптимально и что для любой свободной неизвестной х_j с положительным коэффициентом ∆_j можно указать конечную неотрицательную область ее изменения при нулевых значениях других свободных неизвестных. Скорость изменения целевой функции L относительно независимой переменной х_j при нулевых значениях других свободных неизвестных определяется частной производной . Следовательно наиболее быстро целевая ф-ия будет убывать при возрастании той свободной переменной, при которой в последнем уравнении вспомогательной системы стоит наибольший положительных коэффициент∆_j .

Так неизвестная x_s при нулевых значениях других свободных неизвестных не может возрастать неограниченно, а целевую ф-ю мы хотим минимизировать, то придадим неизвестной x_s наибольше значение, которое она может принять, тем самым выделив из общего решения крайнее неотрицательное решение системы ограничений. Это крайнее решение совпадает с новым базисным неотрицательным решением, соответствующим новому предпочитаемому виду системы, для получения которого достаточно принять неизвестную x_s за разрешающую и подвергнуть систему симплексному преобразованию. Если

m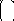in = , то за разрешающее Ур-е берем r-е. как только мы получим новое базисное неотрицательное решение системы ограничений, придется это решение исследовать на оптимальность.

Процесс перехода к новым и новым решениям продолжается до тех пор, пока не будет получено оптимальное решение (или не будет доказана неограниченность линейной формы на множестве решений системы ограничений, но это утверждение справедливо лишь при условии невырожденности задачи, т.е. ни на одном этапе процесса решения ни один из свободных членов системы ур-й не обращается в нуль). Новое значение линейной формы строго меньше предыдущего и через конечное число шагов мы придем к оптимальному решению (или докажем неразрешимость задачи). В вырожденном случае на одном или нескольких этапах свободный член может оказаться равны нулю, и значение линейной формы не измениться. Появится возможность цикла.

19.Применение искусственных базисных неизвестных к решению основной задачи ЛП. Условие противоречивости системы условий исходной задачи. Если задача не имеет предпочитаемого вида х1+a(1,m+1)x(m+1)+…g(1n)xn=h1, x2+g(2,m+1)x(m+1)+…g(2n)xn=h2…, то к ней нельзя применять симплексный метод, поэтому к левой части каждого уравнения системы добавляется по одной искусственной неотрицательной неизвестной, набор который составляет искусственный базис. Вспомогательная целевая функция должна стремиться к минимуму. Для решения вспомогательной задачи уже можно применять симплексный метод. Если Smin>0, то исходная задача не имеет решения ввиду противоречивости условий. Если Smin=0, то искусственный базис=0. Отбрасываем искусственный базис и, рассматривая результат как предпочитаемый эквивалент исходной задачи, приступаем к решению. Эти рассуждения справедливы к невырожденной задаче. Если же задача является вырожденной, то может случиться, что при Smin=0 не все искусственные переменные выведены из базиса. Тогда следует учесть, что правая часть уравнения, содержащего искусственную базисную неизвестную, должна быть равна нулю, и потому мы можем либо отбросить это уравнение, если оно содержит только искусственные неизвестные, либо, если оно содержит хотя бы одну из исходных неизвестных, принять это уравнение за разрешающее и исключить какую-нибудь из этих неизвестных из всех других уравнений, чтобы вытеснить искусственную базисную неизвестную в число свободных, помня, что в случае необходимости можно рассматриваемое уравнение умножить на (-1).

20. Двойственные (расчетные) оценки ресурсов. Симметричная пара двойственных задач ЛП. Несимметричная пара двойственных задач ЛП, правила составления двойственной задачи для данной задачи ЛП со смешанными ограничениями. Рассмотрим ситуацию, когда предприниматель, занимающийся производством каких-то других видов продукции, но с использованием таких же видов ресурсов, какие есть у нас, предлагает нам уступить ресурсы за цены y1,y2…. В данном случае возникает двойственная задача. Величины у1,у2… называют расчетными или двойственными оценками ресурсов. Они зависят от условий, в которых действует наше предприятие. Конкурент не хочет проиграть в цене, а производитель не хочет переплачивать. Объединяя эти условия, получаем двойственную задачу: yb->min, где у – цена, b – ресурсы (расход ресурсов*цену>прибыли от использования). Прямой задачей остается: сx->max (расход ресурсов за изделия*количество изделий<ресурсов).

Двойственная задача получается из исходной след. Образом:

1.Каждому ограничителю-неравенству исходной задачи ставится в соответствие переменная двойственной задачи, принимающая неотрицательные значения.

2.Матрица неизвестных при коэффициентах транспонируется.

3.Правые части ограничений заменяются коэффициентами целевой функции.

4.Меняются направления неравенств, коэффициенты целевой функции заменяются правыми частями ограничений.

5. От максимизации (минимизации) ф-ии цели переходят к минимизации (максим-ии).

Число переменных двойственной задачи равно числу ограничений прямой задачи, а число ограничений двойственной задачи – числу переменных прямой задачи. Оптимальное решение называется вектором «теневых» цен ресурсов.

->max,

, xj>=0 – исходн.задача ->min, ,yi>=0 – двойств. зад.

Говорят, что задачи ЛП образуют симметричную пару. Если же система ограничений содержит как неравенства, так и уравнения, то в двойственной задаче, отвечающая ограничению-равенству, может принимать значения любого значения, а ограничению-неравенству будет соответствовать неотрицательная переменная, т.е. пара двойственных задач может быть записана в виде: ->max, для i=1,k, j=1,l и xj>=0, для i=k+1,m, j=l+1,n, и xj любого знака + тоже для ->min, .