38. Основная теорема теории игр, выражение оптимальных стратегий игроков через решения пары двойственных задач лп.

Основная теорема теории игр:

1. всякая матричная игра имеет решения.

2. решение всякой матричной игры может быть сведено к решению пары симметричных двойственных задач.

Основная теорема: в матричной игре с нулевой суммой у игроков есть оптимальные решения. Решение всякой матричной игры может быть сведено к решению пары симметричных двойственных задач ЛП. Исходная задача (для первого игрока):

->min, ,xi>=0. Двойственная задача (для второго ирока):

->max, ,yj>=0. х=p/гамма, y=q/гамма. Решая эти задачи, найдем цену игру и оптимальные стратегии.

39. Применение математического ожидания и дисперсии дискретной случайной величины при анализе финансовых операций.

Обозначим буквой Q некоторую обобщенную характеристику произвольной финансовой операции. Назовем эту характеристику эффективностью операции. Часто невозможно заранее точно предсказать эффективность той или иной операции, и такие операции рассматривают как случайные величины. При этом в качестве ожидаемой эффективности используют мат.ожидание MQ, а измерителем риска служит среднее квадратическое отклонение r = .

П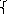усть на финансовом рынке есть возможность осуществить несколько финансовых операций, ожидаемые эффективности и риски которых известны. Говорят что операцияQi доминирует операцию Qj, если MQi >= MQj

ri < rj

Операция Qi называется оптимальной по Парето, если не существует операций, которые бы ее доминировали.

Для графического решения задачи строится система координат, на которой откладывается r(y) и MQ(x) и находится оптимальная точка. Также можно определить оптимальную операцию по взвешивающей формуле, например (Q)=2Q-r, и макс.значение будет соответствовать лучшей операции, мин. – худшей.

41. Графы: основные понятия.

Граф – совокупность точек (вершин) и линий (ребер), соединяющих некоторые пары этих точек. Некоторые ребра снабжаются стрелками, они называются ориентированными ребрами или дугами. Две вершины могут соединяться несколькими ребрами, идущими в одном направлении. Такие ребра называются кратными (параллельными), а граф, содержащий кратные ребра, - мультиграфом. Если у графа вершины соединены дугами – ориентированный граф или сеть, если нет – неориентированный. G=(X,U), Х - непустое конечное множество (множество вершин), U – бинарное отношение на нем (множество ребер). Дуги обозначаются: (xi,xj,v) = начало, конец и номер. Ребра: {(xi,xj,v),(xj,xi,v)}. Вершины, соединенные ребром или дугой, называются смежными. Ребра, имеющие общую вершину, также называются смежными. Ребро инцидентно ее вершинам и вершина ребра инцидента ребру. Вершина, не ициндентная никакому ребру, называется изолированной. Граф, состоящий только из изолированных вершин, называется нуль-графом. Граф называется простым, если он не содержит петель и параллельных дуг. Граф называется полным, если он простой и каждая пара вершин смежна. Полный ориентированный граф называется турниром. Число ребер, инцидентных вершине xi, называется степенью графа.

Вершина на графе, которая следует за всеми вершинами некоторого множества, называется мажорантой. Вершина, предшествующая вершинам некоторого множества, называется минорантой. Граф конечен, если число его вершин конечно. Путь на графе – есть такая последовательность дуг, когда конец каждой предшествующей совпадает с началом следующей. Путь простой, когда никакая дуга не встречается два раза. Матрица смежности графа с n вершинами – матрица порядка n, в которой в случае неориентированного графа aij=k (если вершина xi смежна с xj) или 0 в противном случае, для ориентированного графа aij=k, k – число дуг от вершины xi в xj. Можно получить несколько различных матриц смежностей графа, меняя обозначения его вершин.

43. Задача о кратчайшем пути в графе и ее решение Граф – совокупность точек (вершин) и линий (ребер), соединяющих некоторые пары этих точек. Некоторые ребра снабжаются стрелками, они называются ориентированными ребрами или дугами. Два вершины могут соединяться несколькими ребрами, идущими в одном направлении. Такие ребра называются кратными (параллельными), а граф, содержащий кратные ребра, - мультиграфом. G=(X,U), Х- непустое конечное множество (множество вершин), U – бинарное отношение на нем (множество ребер). Дуги обозначаются: (xi,xj,v) =начало, конец и номер. Ребра: {(xi,xj,v),(xj,xi,v)}. Вершины, соединенные ребром или дугой, называются смежными. Ребра, имеющие общую вершину, также называются смежными.

Индексный метод позволяет найти кратчайший путь (Форда). Каждой вершине, кроме xi присваиваем величину Uj (большое число), а xi=0. Поверяем неравенство: Uj>Ui+uij. Если неравенство выполняется, то j-ой вершине дается новый вес Ui+uij. Если не выполняется, то вес остается старый. Двигаясь по смежным вершинам, пересчитываем вершины и доходим до последней. Новые веса вершин – расстояние от входа до данной вершины. Чтобы найти кратчайший путь, идут обратно, проверяя равенство: Uj=Ui+uij.