- •Взвешенные и структурные средние
- •Средние для дискретного ряда Средняя арифметическая взвешенная
- •Средняя гармоническая взвешенная
- •Средняя геометрическая взвешенная
- •Средняя квадратическая взвешенная
- •Средние для интервального ряда
- •Например, средняя арифметическая для интервального ряда
- •Структурные средние величины
- •Медиана
- •Квантили
- •Квартили
- •Перцентили
Например, средняя арифметическая для интервального ряда
При расчете средней арифметической для интервального вариационного ряда сначала определяют среднюю для каждого интервала, как полусумму верхней и нижней границ, а затем — среднюю всего ряда. В случае открытых интервалов значение нижнего или верхнего интервала определяется по величине интервалов, примыкающих к ним.
Пример 3. Определить средний возраст студентов вечернего отделения.
|
Возраст в годах |
Число
студентов
|
Среднее
значение интервала
|
Произведение
середины интервала (возраст)
на число
студентов |
|
до 20 |
65 |
(18 + 20) / 2 =19 18 в данном случае граница нижнего интервала. Вычисляется как 20 — (22-20) |
1235 |
|
20 — 22 |
125 |
(20 + 22) / 2 = 21 |
2625 |
|
22 — 26 |
190 |
(22 + 26) / 2 = 24 |
4560 |
|
26 — 30 |
80 |
(26 + 30) / 2 = 28 |
2240 |
|
30 и более |
40 |
(30 + 34) / 2 = 32 |
1280 |
|
Итого |
500 |
|
11940 |
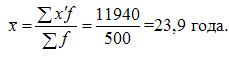
Средние, вычисляемые из интервальных рядов являются приближенными.
Структурные средние величины
Кроме степенных средних в статистике для относительной характеристики величины варьирующего признака и характеристики рядов распределения пользуются структурными средними: модой и медианой.
Мода
Мода— это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей.
Модой для дискретного ряда является варианта, обладающая наибольшей частотой.
При вычислении моды для интервального вариационного ряда необходимо:
сначала определить модальный интервал (по максимальной частоте),
затем — значение модальной величины признака по формуле:
![]()
где:
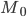 —
значение моды
—
значение моды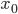 —
нижняя граница модального интервала
—
нижняя граница модального интервалаi — величина интервала
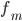 —
частота модального интервала
—
частота модального интервала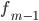 —
частота интервала, предшествующего
модальному
—
частота интервала, предшествующего
модальному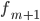 —
частота интервала, следующего за
модальным
—
частота интервала, следующего за
модальным
Определение моды графически: Мода определяется по гистограмме распределения. Для этого
правую вершину модального
прямоугольника соединяют с правым
верхним углом предыдущего прямоугольника
, а левую
вершину модального прямоугольника -
с левым верхним углом
последующего прямоугольника. Абсцисса
точки пересечения этих прямых и будет
модой распределения.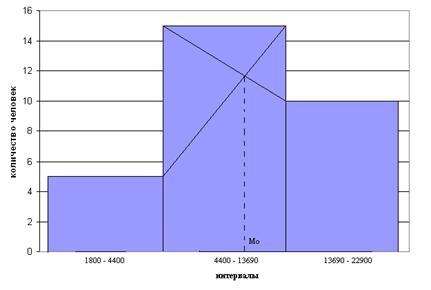
Медиана
Медиана — это значение признака, который делит вариационный ряд на две равные по численности части.
Медиана для дискретного ряда.
Для определения медианы в дискретном
рядус нечетнымколичеством
единиц наблюдения сначалапорядковый
номер медианыпо формуле: ![]() ,
а затем определяют, какое значение
варианта обладает накопленной частотой,
равной номеру медианы.
,
а затем определяют, какое значение
варианта обладает накопленной частотой,
равной номеру медианы.
Если ряд содержит четное
число элементов, то
медиана будет равна средней из двух
значений признака, находящихся в
середине. Номер первого из этих признаков
определяется по формуле: ![]() ,
для второго -
,
для второго - ![]() .
.
![]() = n
(количество элементов в ряду).
= n
(количество элементов в ряду).
Медиана для интервального ряда
При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана.
Для этого:
определяется номер медианы по формуле:
 ,
полученное значение округляется до
целого большего числа.
,
полученное значение округляется до
целого большего числа.затем по накопленной частоте определяется интервал, в который входит элемент с таким номером,
затем — значение медианы по формуле:
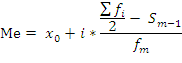
где:
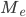 —
искомая медиана
—
искомая медиана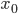 —
нижняя граница интервала, который
содержит медиану
—
нижняя граница интервала, который
содержит медиануi — ширина интервала
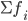 —
сумма частот или число членов ряда
—
сумма частот или число членов ряда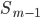 -
накопленная частота интервала,
предшествующего медианному
-
накопленная частота интервала,
предшествующего медианному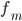 —
частота медианного интервала
—
частота медианного интервала
Пример. Найти моду и медиану для интервального ряда.
|
Возрастные группы |
Число студентов |
Сумма накопленных частот ΣS |
|
До 20 лет |
346 |
346 |
|
20 — 25 |
872 |
1218 |
|
25 — 30 |
1054 |
2272 |
|
30 — 35 |
781 |
3053 |
|
35 — 40 |
212 |
3265 |
|
40 — 45 |
121 |
3386 |
|
45 лет и более |
76 |
3462 |
|
Итого |
3462 |
|
Решение:
Определим моду
В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на этот интервал приходится наибольшая частота (1054).
Рассчитаем величину моды:
![]()
Это значит, что модальный возраст студентов равен 27 годам.
Определим медиану.
Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части (Σfi/2 = 3462/2 = 1731). Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:
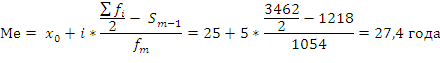
Это значит, что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.
Графически медиана определяется по кумуляте. Для ее определения высоту наибольшей ординаты, которая соответствует сумме всех частот, делят пополам. Через полученную точку
проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой.