Взвешенные и структурные средние

Средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности. Средние величины исчисляются для характеристики уровня цен, заработной платы, основного капитала, численности населения и др. однородной совокупности социально-экономических явлений.

Требования, предъявляемые к средним величинам:

-  средняя должна характеризовать качественно однородную совокупность;

-  средние должны исчисляться по данным большого числа единиц, составляющих совокупность, то есть отображать массовые социально-экономические явления.

Средняя величина всегда именованная, она имеет ту же размерность, что и признак у единиц совокупности (т.е всегда единицы измерения средней такие же, как у единиц наблюдения, для которых вычисляется средняя).

В исследованиях применяются две категории средних: степенные средние и структурные средние.

К степенным средним относятся: средняя арифметическая, средняя гармоническая, средняя геометрическая и средняя квадратическая. Средняя обозначается через . Черта вверху символизирует процесс осреднения индивидуальных значений. Частота – повторяемость отдельных значений признака – обозначается буквой f.

1. Средние для дискретного ряда Средняя арифметическая взвешенная

Если объем совокупности данных большой и представляет собой ряд распределения, то исчисляется взвешенная среднеарифметическая величина. Она используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.

Формула средней арифметической взвешенной:

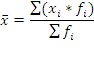
Пример 1. Найти среднюю заработную плату рабочих цеха за месяц

Заработная плата одного рабочего тыс.руб; X	Число рабочих F
3,2	20
3,3	35
3,4	14
4,0	6
Итого:	75

Средняя заработная плата может быть получена путем деления общей суммы заработной платы на общее число рабочих:

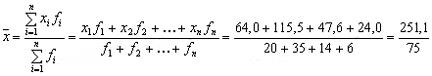
Ответ: 3,35 тыс.руб.

Средняя гармоническая взвешенная

Средняя гармоническая — используется в тех случаях, когда известны индивидуальные значения признакаи произведение, ачастотынеизвестны.

Формула средней гармонической взвешенной:

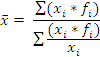
Пример 2. Вычислить среднюю урожайность по трем фермерским хозяйствам

В примере ниже  (урожайность одного гектара земли) - известна,  — площадь неизвестна (хотя её можно вычислить делением валового сбора зерновых на урожайность),  — валовый сбор зерна известен.

Фермерское хозяйство	Урожайность ц/га (х)	Валовый сбор зерновых Ц (z = x*f)
1	18,2	3640
2	20,4	3060
3	23,5	2350
Итого		9050

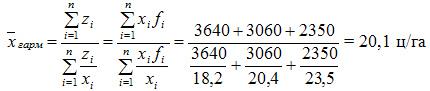
Ответ: 20,1 ц/га

Средняя геометрическая взвешенная

Для определения средней геометрической взвешенной применяется формула:

, , ,

Где – первый уровень (первое значение) ряда динамики,

- второй уровень (второе значение) ряда динамики,

– третий уровень (третье значение) ряда динамики,

- предпоследний уровень ряда динамики,

– последний уровень ряда динамики,

– частоты цепных индексов x₁, x₂, x₃…

Средняя квадратическая взвешенная

Средняя квадратическая взвешенная равна:

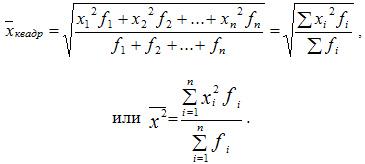
2. Средние для интервального ряда

Для вычисления средней в интервальных рядах нужно перейти к дискретному ряду, то есть заменить интервал его средним значением и дальнейшие вычисления производить по формулам для дискретного ряда.

Среднее значение интервала (середина интервала) определяется как среднее арифметическое между верхней и нижней границами интервала:

,