
- •Структура рабочей тетради
- •Введение Пояснительная записка
- •Тематический план
- •Рекомендации по работе с математическим текстом
- •Рекомендации по конспектированию
- •Рекомендации по решению задач
- •Раздел 1. Теория пределов
- •Предел функции
- •Первый и второй замечательные пределы.
- •- Второй замечательный предел
- •Непрерывность функции Непрерывность функции в точке
- •Односторонние пределы функции*
- •Точки разрыва и их классификация*
- •Устранимый разрыв
- •Вопросы для самоконтроля
- •Контрольные задания
- •Раздел 2. Дифференциальное исчисление функции одной переменной
- •Производная функции одной переменной. Правила дифференцирования. Производная сложной функции
- •Геометрический смысл производной
- •Механический смысл производной
- •Правила дифференцирования
- •Формулы дифференцирования
- •Производная сложной функции
- •Дифференциал
- •Производные и дифференциалы высших порядков
- •Исследование функции при помощи дифференциального исчисления
- •Вопросы для самоконтроля
- •Контрольное задание
- •Раздел 3. Интегральное исчисление функции одной переменной
- •Первообразная функции. Неопределенный интеграл и его свойства.
- •Приемы интегрирования
- •Вопросы для самоконтроля
- •Контрольное задание
- •Определенный интеграл
- •Геометрические приложения определенного интеграла
- •Вопросы для самоконтроля
- •Контрольное задание
- •Раздел 4. Ряды
- •Основные понятия
- •Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами.
- •Знакопеременные и знакочередующиеся ряды. Абсолютная и условная сходимость. Признак Лейбница для знакочередующихся рядов.
- •Вопросы для самоконтроля
- •Контрольное задание
- •Раздел 5. Основы теории вероятностей и математической статистики.
- •Основные понятия комбинаторики
- •Вопросы для самоконтроля
- •Контрольное задание
- •Классическое определение вероятности
- •Вопросы для самоконтроля
- •Контрольное задание
- •Случайные величины
- •Числовые характеристики случайной величины
- •Вопросы для самоконтроля
- •Контрольное задание
- •Литература
Односторонние пределы функции*
Левосторонний предел функции. Если отыскивается предел функцииf(x)при условии, чтох, стремясь ка,может принимать только такие значения, которые меньшеа, то этот предел, если он существует, называется левосторонним пределом функцииf (х)(или левым пределом функции).
Для того чтобы показать, что х стремится
ка, оставаясь меньшеа,
употребляется запись:![]() ,
а левосторонний предел функции
обозначается символом:
,
а левосторонний предел функции
обозначается символом:![]() .
.
Правосторонний предел функции. Если отыскивается предел функцииf(x)при условии, чтох, стремясь ка, может принимать только такие значения, которые большеа, то этот предел, если он существует, называется правосторонним пределом функцииf(x)(или правым пределом функции).
То, что х,стремясь ка, остается
большеа, обозначается так:![]() ,
а правосторонний предел функции
обозначается символом:
,
а правосторонний предел функции
обозначается символом:![]() .
.
Очевидно, что предел функции при
![]() существует только тогда, когда существуют
и равны между собой ее левосторонний и
правосторонний пределы, т. е. когда
существует только тогда, когда существуют
и равны между собой ее левосторонний и
правосторонний пределы, т. е. когда![]()
![]() .
.
Определение Функция f(x) называется непрерывной при х = а, если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, т. е. f(a). То есть:
![]()
![]() .
.
Точки разрыва и их классификация*
Если равенство
![]()
![]() в какой-либо его части не выполняется,
то о точке
в какой-либо его части не выполняется,
то о точке![]() говорят,
что она является точкой разрыва.
говорят,
что она является точкой разрыва.
Точка разрыва первого рода
|
Р |
Определение. Если левосторонний предел функции и ее правосторонний предел существуют, но не равны, между собой, т. е. если
то точка а называется точкой разрыва первого рода(см. рис. 2). |
Точка разрыва второго рода
|
а |
Определение. Если в точке х = а не существует конечный левосторонний или правосторонний предел функции или оба одновременно, то эта точка называется точкой разрыва второго рода. На рис. 3, аотсутствует левосторонний предел функции; на рис. 3,б– нет правостороннего предела функции. |
|
Рис. 3 |
|
Рис. 4
|
На рис. 4 представлен график функции, которая не имеет в точке х = ани левостороннего, ни правостороннего предела. Во всех этих случаях говорят, что функция в точкех = атерпит разрыв второго рода (иначе: точках = а— точка разрыва второго рода).
|
Устранимый разрыв
Определение. Если в точке х = а функция f(x) имеет левосторонний и правосторонний пределы и эти пределы между собой равны, но их значения не совпадают со значением функции в точке а, т. е. со значением f(a), то точка х = а называется точкой устранимого» разрыва.
Таким образом, в этом случае
![]()
![]() .
Разрыв «устраняется» тем, что полагают
.
Разрыв «устраняется» тем, что полагают![]()
![]() ,
т. е. принимают, что
,
т. е. принимают, что![]() .
.
Пример.Пользуясь определением
непрерывности функции через предел![]() ,
докажем, что функция
,
докажем, что функция![]() непрерывна
в произвольной точке.
непрерывна
в произвольной точке.
Решение. Выразим приращение функции при произвольном приращении аргумента в некоторой точкех:
![]()
Подставим полученные выражения в формулу приращения функции, и после упрощения получим:
![]() .
.
Найдем предел приращения функции при приращении аргумента, стремящемся к 0:
![]()
В итоге получаем, что при любом значении хпредел приращения функции равен нулю, что доказывает ее непрерывность при любом значениих.
Пример.Исследуем на непрерывность прих= 1 следующую функцию:
 .
.
Решение. Так как знаменатель
![]() дроби равен нулю при
дроби равен нулю при![]() ,
то функция разрывна при
,
то функция разрывна при![]() .
Установим характер этой точки разрыва.
Найдем сначала левосторонний предел
функции:
.
Установим характер этой точки разрыва.
Найдем сначала левосторонний предел
функции:
Если
![]() ,
то можно представить
,
то можно представить![]() ,
,![]() и считать, что
и считать, что![]() ,
оставаясь положительной, стремится к
нулю. Заменяяхна
,
оставаясь положительной, стремится к
нулю. Заменяяхна![]() ,
получим:
,
получим:

так как при
![]() величина
величина![]() бесконечно
большая,
бесконечно
большая,![]() также
бесконечно велика,
также
бесконечно велика,![]() –
бесконечно большая величина, обратная
ей величина
–
бесконечно большая величина, обратная
ей величина![]() бесконечно мала:
бесконечно мала: ,
а потому
,
а потому
Теперь определим правосторонний предел функции. Если х →1 + 0, можно положить х = 1 + α (α > 0) и считать, что α, оставаясь положительной, стремится к нулю.
Тогда, заменяя хна 1 + α, получим:
 ,
,
т
.)
![]() величина
величина![]() бесконечно
большая,
бесконечно
большая,![]() также
бесконечно велика,
также
бесконечно велика,![]() – величина бесконечно малая, т.е. ее
предел будет равен 0.
– величина бесконечно малая, т.е. ее
предел будет равен 0.
Итак, у функции существуют и левосторонний
предел, равный 2, и правосторонний предел,
равный 3, но между собой они не равны. Из
этого мы заключаем, что точка
![]() является для заданной функции точкой
разрыва первого рода.
является для заданной функции точкой
разрыва первого рода.
Пример.Построим графики и определим, какого рода разрыв имеет функция в данной точке (если точка не указана, определим точки разрыва самостоятельно):
1)
![]() ,
,![]() 2)
2)![]() 3)
3)![]() .
.
Решение.
в точке
 функция имеет разрыв второго рода,
поскольку не имеет в этой точке ни
одного конечного предела (см. рис. 5,а).
функция имеет разрыв второго рода,
поскольку не имеет в этой точке ни
одного конечного предела (см. рис. 5,а).в точке
 функция имеет разрыв второго рода,
поскольку не имеет в этой точке ни
одного конечного предела (см. рис. 5,в).
функция имеет разрыв второго рода,
поскольку не имеет в этой точке ни
одного конечного предела (см. рис. 5,в).функция имеет точки разрыва
 и
и .
В обеих точках функция имеет разрыв
второго рода (см. рис. 5,б).
.
В обеих точках функция имеет разрыв
второго рода (см. рис. 5,б).
|
|
| |
|
а) |
б) |
в) |
|
Рис. 5 | ||

 ис.
2
ис.
2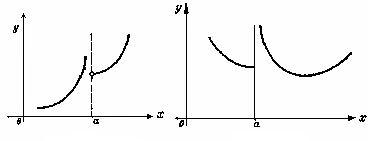 )
б)
)
б)


