Первый и второй замечательные пределы.

Рис. 1

Первый замечательный предел. Вывод первого замечательного предела представляет интерес с точки зрения приложения теории пределов, и поэтому мы предлагаем Вам его практически целиком. Рассмотрим поведение функции при. Для этого рассмотрим окружность радиуса 1; обозначим центральный угол МОВ черезх, при этом.

Тогда явно площадь DМОА < площадь сектора МОА < площадьDСОА (см. рис. 1).

S _DМОА =

S _МОА==S_DCОА=

Вернувшись к упомянутому неравенству и удвоив его, получим:

sin x < x < tg x.

П

осле почленного деления наsinx: или

Поскольку , то переменнаязаключена между двумя величинами, имеющими один и тот же предел, т.е. , на основании теоремы о пределе промежуточной функции предыдущего пункта имеем:

-первый замечательный предел.

Пример.Вычислите пределы функций, используя первый замечательный предел:

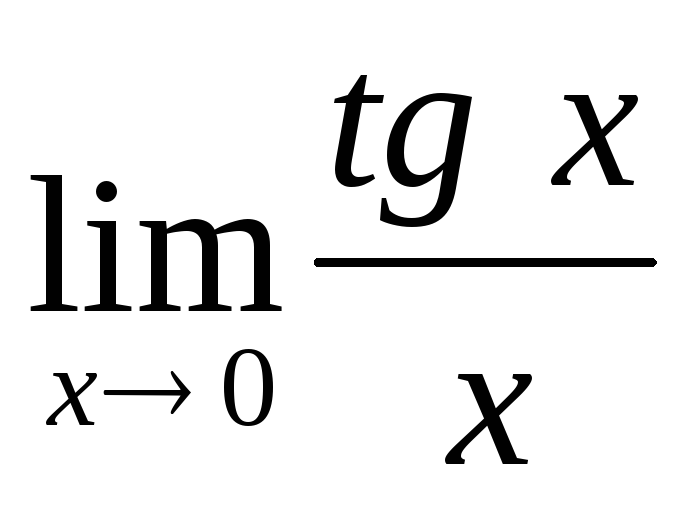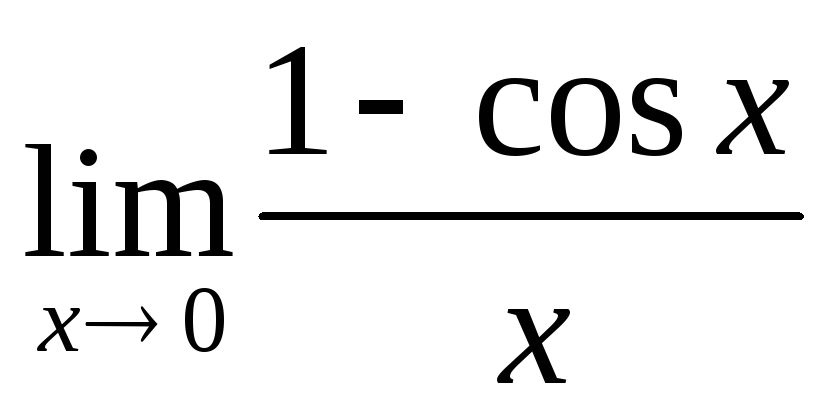1. ; 2) ; 3)

Решение.

1. Разложим как отношениеи объединим множители по вышеуказанной схеме:

2. Применяя формулу , произведем подстановку и получим:

3. Разделим числитель и знаменатель дроби на х, затем выровняем сложные аргументы, компенсируя преобразование добавочным коэффициентоми получим:

Ответ.1) 1, 2) 0, 3)

Задание: Вычислите предел функции, используя первый замечательный предел:

Решение:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________Ответ:-2.

Второй замечательный предел.

Для вывода второго замечательного предела введем определение числа е:

Определение. Предел переменной величины приназывается числоме:

- Второй замечательный предел

Число е– иррациональное число. Его значение с десятью верными знаками после запятой обычно округляют до одного верного знака после запятой:

e= 2,7182818284…»2,7.

Теорема. Функция прих, стремящемся к бесконечности, стремится к пределу е:

Пример.Вычислите пределы функций:

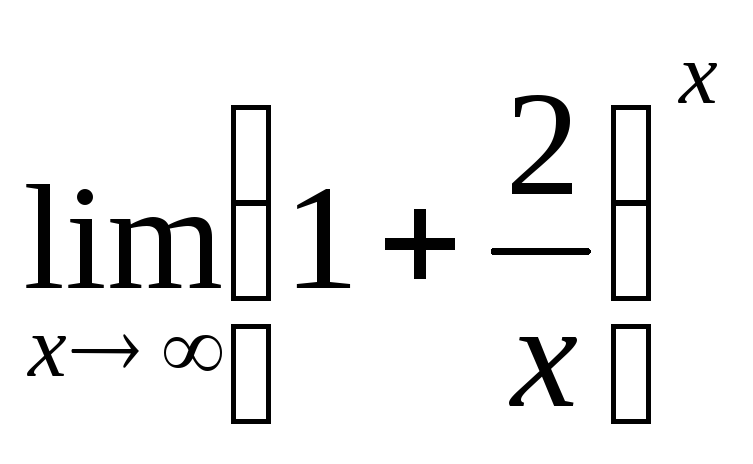1. 2) ; 3)

Решение.

1. С

   огласно свойствам пределов, предел степени равен степени предела, т. е.:

2. Введем новую переменную с целью свести предел ко второму замечательному пределу: , отсюда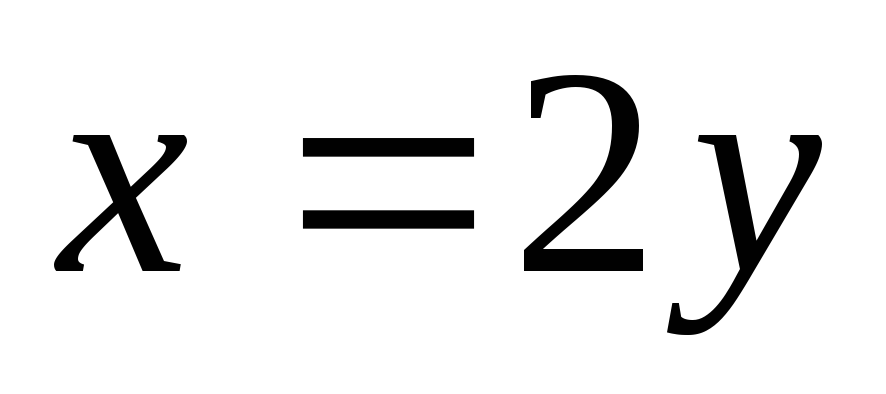. Приимеем, т. е..

Кроме того, аналогичным образом можно доказать, что

3. Разложив числитель данной дроби на слагаемые, добьемся выделения 1, а затем примем 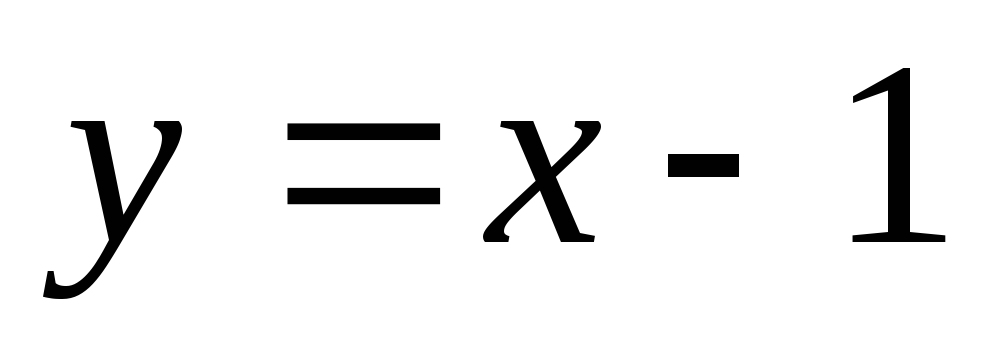и используем упомянутое выше утверждение:

Ответ.1)е³, 2) е², 3)е⁴.

Задание. Вычислите предел функции, используя второй замечательный предел:

Решение:

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Ответ: е^-5

Непрерывность функции Непрерывность функции в точке

Определение. Функция f(x), xÎ (a; b) называется непрерывной в точке x_оÎ (a; b), если предел функции f(x) в точке х_о существует и равен значению функции в этой точке:

.

Согласно данному определению, непрерывность функции f(x)в точкех_оозначает выполнимость следующих условий:

1. функция f(x)должна быть определена в точкех_о;

2. у функции f(x)должен существовать предел в точкех_о;

3. предел функции f(x)в точкех_одолжен совпадать со значением функции в этой точке.

Пример.

Функция f(x) = x²определена на всей числовой прямой и непрерывна в точкех = 1 посколькуf(1)= 1 и

Непрерывность функции на множестве

Определение. Функция f(x), называется непрерывной на интервале (a; b), если она непрерывна в каждой точке этого интервала.

Если функция непрерывна в некоторой точке, то эта точка называется точкой непрерывности данной функции. В тех случаях, когда предел функции в данной точке не существует или его значение не совпадает со значением функции в данной точке, то функция называется разрывной в этой точке, а сама точка – точкой разрыва функции f(x).

Свойства непрерывных функций.

1) Сумма конечного числа функций, непрерывных в точке а,есть функция, непрерывная в этой точке.

2) Произведение конечного числа функций, непрерывных в точке а,есть функция, непрерывная в этой точке.

3) Отношение конечного числа функций, непрерывных в точке а,есть функция, непрерывная в этой точке, если значение функции, стоящей в знаменателе, отлично от нуля в точкеа.

Пример.

1. Функция f(x) = x^п, гдеn Î N, непрерывна на всей числовой прямой. Доказать этот факт можно, используя свойство 2 и непрерывность функцииf(x) = x.

2. Функция f(x) = сx^п(с– константа) непрерывна на всей числовой прямой, исходя из свойства 2 и примера 1.

Т

еорема 1. Многочлен есть функция, непрерывная на всей числовой прямой.

Теорема 2. Любая дробно-рациональная функция непрерывна в каждой точке своей области определения.

Пример.

1. Функция непрерывна на всей числовой прямой, кроме точки, в которой знаменатель дроби обращается в нуль.

2. Ф

   ункциянепрерывна всюду наR, т.к. знаменатель нигде не обращается в нуль.

Определение Функция f(x) называется непрерывной в точке х = а, если в этой точке ее приращение стремится к нулю, когда приращение аргументастремится к нулю, или иначе: функцияf (х) называется непрерывной в точке х = а , если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е. если