
Виды информации.
В процессе прохождения информации по дискретному каналу, данные многократно применяют свою форму, сохраняя содержание данных:
-
непрерывные (аналоговые) данные;
-
цифровые (дискретные) данные;
-
криптографический код;
-
оптимальные коды;
-
помехоустойчивые коды;
-
электрические сигналы;
Цифровые, информационные технологии, обеспечивают высокую надежность, достоверность и эффективность передачи данных.
-
Количество информации и энтропия
S= у моей мамы золотые руки
ls = 24;
Алфавит сообщения;
А={у _моейаызлтрки}
la = 14;
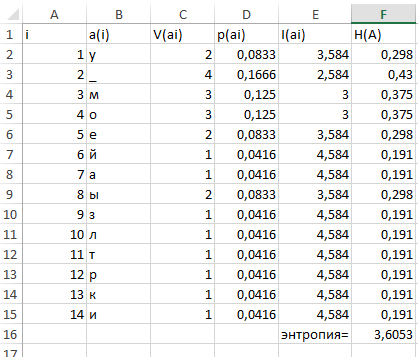
Расчет энтропии алфавита;
H max(A) = log la la= 9
H max (14) = log2p(14) = 3,807355 [бит/симв]
Расчет энтропии сообщения;
H(А) = ∑ vi*H(ai)= 3,6053 [бит/симв]
Расчет максимальной энтропии;
H max(X) = log ls ls = 24
H max(X) = log (24) = 4,584963 [бит/симв]
Свойства энтропии
-
Энтропия неотрицательна H(A)>0
-
Энтропия равна 0 тогда и только тогда, когда вероятность равна 1: H(A)=0 P(ai)=1
-
Энтропия ограничена H(A)>log n
-
Максимальная энтропия равна Hmax(X)=log n
Графики
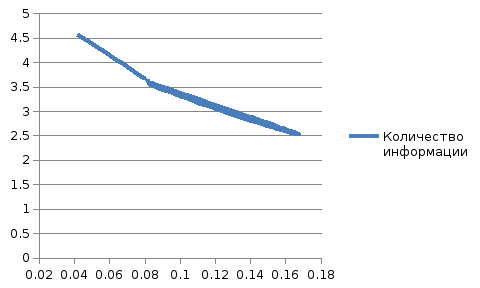
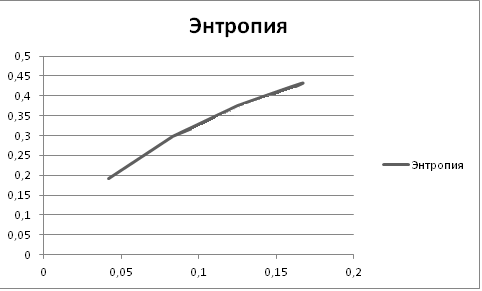
-
Способы задания дискретного канала
1) Со стороны источника
![]()
Дискретный
канал полностью задан со стороны
источника, если даны: дискретный ансамбль
сообщений источника ДАС={А,
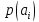 }и
канальная матрица источника КМИ=
}и
канальная матрица источника КМИ=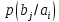
2) Со стороны приемника

Дискретный
канал полностью задан со стороны
приемника, если даны: дискретный ансамбль
сообщений приемника ДАС={В,
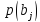 }
и канальная матрица приемника КМП=
}
и канальная матрица приемника КМП=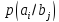
3)
Дискретный канал полностью задан
канальной матрицей объединения (КМО).
КМО=
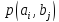
Из
КМО легко вычислить безусловные
вероятности источника
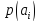 и безусловные вероятности приемника
и безусловные вероятности приемника
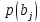
-
Информационные характеристики дискретного канала связи
(Рассмотрим на примере решения задачи)
Дана: канальная матрица условных вероятностей, которые отображают действие помех дискретного канала связи.
 ,
,
Время передачи одного символа = 0,0025 сек. Дать определение и формулы показателей и вычислить все информационные характеристики реального канала связи, включая I (ai), H (A), H (B / ai), H (B / A), H (B), I (A, B), n, H '(A), Kэ, Rкр., скорость передачи R и емкость C канала связи, если передано сообщение из 200 символов.Проверить выполнение теорем Шеннона про скорость передачи и про кодирование. Сделать вывод про надежность и эффективность канала связи.
-
Канальная матрица объединения отражает действие помех на линии связи.
КМО>> КМИ
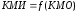
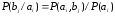

-
Безусловные вероятности появления сигналов на выходе источника сообщений:
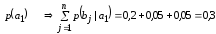
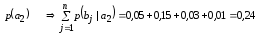

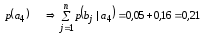
-
Количество информации I(ai) каждого символа a1, a2, a3, a4 дискретного сообщения A :
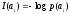 (i=1,2,3),
[бит]
(i=1,2,3),
[бит]
 [бит]
[бит]
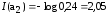 [бит]
[бит]
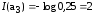 [бит]
[бит]
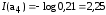 [бит]
[бит]
-
Среднее количество информации, переданой одним символом определяет энтропия источника сообщений Н(А):
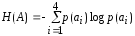 [бит/символ]
[бит/символ]
H(A) = 0,3*1,73+0,24*2,05 +0,25*2 +0,21*2,25 = 1,98 [бит/символ]
-
Максимальная энтропия сообщений Hmax(A)
Hmax(A)= log N=log 4= 2 [бит/символ]
-
Информационные потери при передаче каждого символа ai определяет частная условная энтропия источника H(B/ai ):
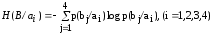 [бит/символ],
[бит/символ],
H(B/a1 )= - (0,8 log 0,8 + 0,2 log 0,2 +0,2 log 0,2) = 0,2575+0,4643+0,4643=1,18
[бит/символ]
H(B/a2 )= - (0,2 log 0,2 +0,6 log 0,6 + 0,12 log 0,12+0,04 log 0,04) =
= 0,4643 + 0,4421 + 0,367 + 0,1857 = 1,4591 [бит/символ]
H(B/a3 )= - (0,8 log 0,8 + 0,2 log 0,2) = 0,2575+0,4643 = 0,7218 [бит/символ]
H(B/a4 )= - (0,2 log 0,2+0,64 log 0,64) = 0,4643 +0,4120= 0,8763 [бит/символ]
-
Средние потери информации при передаче одного символа определяет общая условная энтропия источника Н(B/А):
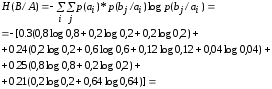
=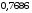 [бит/символ]
[бит/символ]
-
Среднее количество информации, полученная приемником на один символ с учетом потерь информации пораженной помехами, I(A,B)
I (A, B) = H (А) - H (B / A) бит/символ.
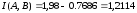 бит/символ
бит/символ
-
Безусловные вероятности появления сигналов на входе приемника сообщений:
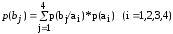
 Проверим,
составляют ли вероятности p(bj)
полную группу, то есть
Проверим,
составляют ли вероятности p(bj)
полную группу, то есть
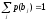
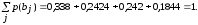
-
Энтропия приемника сообщений Н(B):
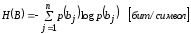
|
P(bj) |
-log p(bj) |
|
0,338 |
1,564905 |
|
0,2424 |
2,044538 |
|
0,242 |
2,046921 |
|
0,1844 |
2,439089 |
Н(B)=0,338*1,564 + 0,2424*2,044 + 0,242*2,046 + 0,1844*2,439 = 1.96
-
Максимальная энтропия сообщений Hmax(B):
Hmax(B)= log N=log 4= 2 [бит/символ]
-
Скорость модуляции дискретного источника сообщений, n
n=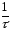 ,
симв/сек.
,
симв/сек.
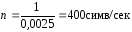
-
Производительность дискретного источника сообщений, H’(A)
H’(A)=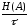 бод.
бод.
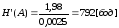
-
Скорость передачи информации, R
R=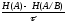 або R=
або R=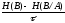
в нашем случае скорость равна:
R=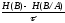 бод
бод
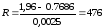 бод
бод
-
Пропускная способность (емкость) С дискретного канала связи определяется максимальной скоростью передачи C=max R
С=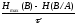
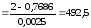
-
Коэффициент эффективности дискретного канала связи, Kэ
Kэ=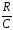
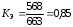
-
Критическая скорость передачи Rкр
Rкр= бод.
бод.
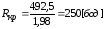
Оценка надёжности и эффективности дискретного канала связи:
1. Теорема Шеннона про скорость передачи
R<Rкр
476 < 250 не выполняется
2. Теорема Шеннона по кодирование
H’(A) < C
792 < 492,5 не выполняется
Рекомендации по повышению надёжности и эффективности:
-
Из-за невыполнения теоремы о скорости передачи невозможным становится восстановление исходного сообщения.
-
Существует способ кодирования и декодировании информации, при котором вероятность ошибки может быть сколь угодно велика. Для увеличения значения С, мы должны увеличить количество символов сообщения.
-
Теоремы Шеннона не выполняются, а значит наш канал связи не является эффективным и надежным
-
Оптимальное кодирование
2.1. Назначение ОНК, цели сжатия
Основной характеристикой дискретного канала связи является скорость передачи данных. При избыточности переданного сообщения скорость передачи уменьшается. Для исключения избыточности сообщения используют математические, и программные средства компрессии данных без потерь содержания информации, в том числе оптимальное кодирование.
Оптимальное кодирование применяется для сжатия (компрессии данных), что позволяет эффективно использовать память ЭВМ, выполнять архивацию данных, уменьшить длительность, и увеличить скорость передачи сообщений, уменьшить действие помех на информацию.
Основная идея оптимального кодирования заключается в том, что символам сообщения, которые имеют большую вероятность, присваиваются короткие бинарные коды, то есть образуются бинарные кодовые слова разной длины - неравномерные коды. Оптимальным неравномерным кодом (ОНК) называется такой код, для которого средняя длина кода является минимальной.
Оптимальное кодирование позволяет:
-
сжимать данные (компрессия);
-
снижать время передачи данных при той же скорости;
-
уменьшать возможные потери и искажения информации;
-
архивировать данные, эффективно использовать помять.
