
3.5. Деревья и их представление
3.5.1. Определения и свойства
Определение.
Конечное корневое
дерево T - это непустое множество
упорядоченных узлов, таких что существует
один выделенный узел, называемый корнем
дерева, а оставшиеся узлы разбиты на
m![]() 0
поддеревьев Т1,Т2,...,Тm.
Узлы, не имеющие поддеревьев, называются
листьями;
остальные узлы называются внутренними.
0
поддеревьев Т1,Т2,...,Тm.
Узлы, не имеющие поддеревьев, называются
листьями;
остальные узлы называются внутренними.
Пример 3.3. На рис. 3.9 изображено дерево с одиннадцатью узлами, помеченными буквами от А до К. Узлы с метками D, E, F, H, J и K являются листьями; другие узлы внутренние. Узел А - корень.
П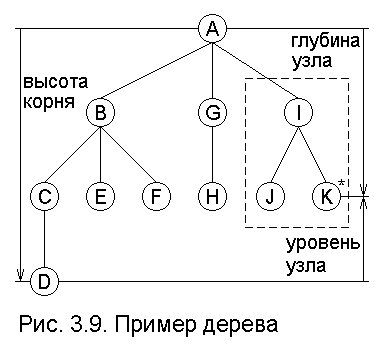 осредством
деревьев изобра-жаются иерархические
организации в комбинаторных алгоритмах,
поэтому они являютсянелинейными
структурами
данных.
осредством
деревьев изобра-жаются иерархические
организации в комбинаторных алгоритмах,
поэтому они являютсянелинейными
структурами
данных.
Для описания соотношений меж-ду узлами дерева используется тер-минология, принятая в генеалогиче-ских деревьях.
Так, в дереве (или поддереве) все узлы являются потомками его корня, и наоборот, корень - предок всех своих потомков. Корень именуется отцом корней его поддеревьев, которые в свою очередь будут сыновьями корня. На рис. 3.9 узел А является отцом узлов B, G и I; J и K - сыновья I, а C, E, F - братья; пунктиром выделено поддерево с узлами I, J, K.
Все рассматриваемые деревья будут упорядочены, т.е. для них будет важен относительный порядок расположения следования каждого узла. Таким образом, деревья, представленные на рис. 3.10,а и б, счи-таются различными.
Для дерева вводятся следующие характеристики:
глубина узла v в дереве - это длина пути из корня в v;
высота узла в дереве - это длина самого длинного пути из v в какой-нибудь лист;
высотой дерева называется высота его корня;
уровень узла v в дереве равен разности высоты дерева и глубины узла v.
Например, на рис. 3.9 высота дерева равна 3; узел К имеет глубину 2, высоту 0 и уровень 1.
Определение.
Лес - упорядоченное множество деревьев.
В связи с этим можно переопределить
понятие дерева: дерево есть непустое
множество узлов, такое, что существует
один выделенный узел, называемый корнем
дерева, а оставшиеся узлы образуют лес
с m![]() 0
поддеревьями корня.
0
поддеревьями корня.
В ажной
разновидностью корневых деревьев
является класс бинарных (двоичных)
деревьев.
ажной
разновидностью корневых деревьев
является класс бинарных (двоичных)
деревьев.
Определение. Бинарное дерево Т либо пустое, либо состоит из выделенного узла, называемого кор-нем, и двух бинарных поддеревьев: левого Т1 и правого T2. Бинарные деревья не являются подмножеством множе-ства деревьев, они полностью отличаются по своей структуре, поскольку две следующие картинки (в и г на рис. 3.10) не изображают одно и то же бинарное дерево. Как деревья, однако, они обе неотличимы от картинки д.
Различие между деревом и бинарным деревом состоит в том, что дерево не может быть пустым, и каждый узел дерева может иметь произвольное число поддеревьев; в то же время бинарное дерево может быть пустым, каждый из его узлов может иметь 0, 1 или 2 поддерева, и существует различие между левыми и правыми поддеревьями.
Определение. Бинарное дерево называется полным, если для некоторого целого k каждый узел глубины меньше k имеет как левого, так и правого сына, а каждый узел глубины k является листом. Полное бинарное дерево высоты k имеет ровно 2k+1–1 узлов.
Определение. Неориентированным деревом называется неориен-тированный ациклический связанный (любые два узла соединены путем) граф. Корневое неориентированное дерево - это неориентированное дерево, в котором узел выделен в качестве корня.
Ориентированное дерево можно превратить в корневое неориен-тированное, просто сделав все его ребра неориентированными. Обычно используют одну и ту же терминологию и применяют одни и те же обоз-начения для корневых неориентированных и ориентированных деревьев. Основное математическое различие здесь состоит в том, что все пути в ориентированном дереве идут от предков к потомкам, тогда как в корне-вом неориентированном дереве пути могут идти в обоих направлениях.
