Основы теории алгоритмов (теория) / Основаная часть / Прил. Б

О.Н. Паулин. Основы теории алгоритмов

Приложение Б

Элементы комбинаторики

Комбинаторика связана с построением, изучением свойств и расчётом числа наборов конечного множества, используемых при решении задач дискретной математики.

Набор¹ r элементов называется r-сочетанием, если принимаются во внимание только элементы без учёта порядка. Наборы могут допускать или не допускать повторения элементов.

При наборах с повторениями различают два случая.

В первом случае предполагается, что запас повторяющихся элементов ограничен и определяется спецификацией {n₁, n₂,…, n_k}, где n_i — количество элементов i-го вида. Общее число элементов исходного множества n=n₁+n₂+…+n_k, причём в r-выборке r  n.

Пример 1. Исходное множество задано тремя элементами a, b, c и спецификацией {2, 2, 1}. Тогда выборки aabb, aabc, abbc являются 4-соче-таниями (3 варианта), а набор aabbc — 5-сочетанием (только одно).

Во втором случае запас элементов не ограничен, и в наборе из r элементов допускается любое число повторений, не превышающее заданного числа r. Исходное множество можно рассматривать как такое, которое состоит из различных элементов, но после выбора некоторого элемента из множества он восстанавливается в нём (набор с возвращением).

При комбинаторных вычислениях используют два правила (называемых золотыми) для определения мощности множеств.

Правило произведения: если некоторый выбор А можно осуществить N вариантами, а для каждого из них некоторый другой выбор В можно реализовать М вариантами, то выбор «А и В» (в указанном порядке) можно произвести NМ вариантами.

Правило суммы (для числа элементов множеств): пусть N(A), N(B), N(C) – соответственно мощности множеств А, В, С. Тогда для вычисления мощности N(A  В  C) используется формула:

N(A  B  C) = N(A) + N(B) + N(C) –

– (N(AB)+N(AC)+N(BC)+

+ N(ABC)). (1)

Если множества А, В, С не пересекаются, то

N(A  B  C ) = N(A) + N(B) + N(C). (2)

Конечное множество с точки зрения комбинаторных вычислений определено числом элементов X={x₁, x₂,..., x_n}, причём элементы x_i - различны. В конкретных комбинаторных задачах формулируются свойства, которым должны удовлетворять решения – наборы элементов конечного множества. Для каждой задачи эти свойства специфичны, однако выделяют 3 основны[ свойства наборов, которые следует учитывать во всех задачах: число элементов, возможность упорядочивания элементов и допущение повторения элементов.

Существует шесть основных типов наборов комбинаторики.

1. Размещения. Это наборы, содержащие к различных элементов, выбранных из n-элементного множества с учётом порядка расположения элементов.

Первый элемент множества выбран n вариантами, второй — n-1 вариантами, ..., k-й элемент — (n-k+1) вариантами. По правилу произведения имеем

= n(n-1)(n-2)...(n-k+1)=. (3)

Пример 2. Приведём трехбуквенные размещения на множестве букв {a,b,c,d}: abc, abd, acd, bcd, ..., bac, bad, ..., dca, dcb — всего 24 варианта.

2. Размещения с повторениями. Это наборы, содержащие к элементов n-элементного множества, поcтроенные с учётом порядка расположения элементов и допускающие повторение элементов.

Первый элемент множества выбран n вариантами, остальные (повтор разрешён) — тоже n вариантами:

=nn...n=n^k. (4)

Пример 3. Для предыдущего примера допустим повторения. Тогда трёхбуквенные размещения на множестве букв {a, b, c, d} будут aaa, aab, aаc, aаd, bаа, ..., bcc, bсd, ..., ddd — всего 64 варианта.

3. Перестановки. Это наборы, получаемые различным упорядочиванием (перестановкой) элементов исходного множества.

Очевидно, перестановки — это размещения для k=n элементов

P_n== = = n! (5)

Пример 4. Для множества {a, b, c} имеем abc, acb, bac, bca, cab, cba – всего 6 вариантов.

4. Перестановки с повторениями. Это набор из m элементов, в котором каждый элемент x_i повторяется n_i раз и при повторении которого учитывается порядок расположения различных элементов; имеется к групп повторяющихся элементов, k  n.

Сначала считаем все m элементов различными, тогда Р_m=m!, затем различие для первого элемента убираем; тогда перестановки, отличающиеся только порядком расположения первого элемента, очевидно, становятся неразличимыми. Перестановок первого элемента будет =n₁!, поэтому

= = .

Рассуждая аналогичным образом для второго, третьего и т.д. элементов, получаем формулу

= , где m=. (6)

Пример 5. Перестановки, полученные различным расположением букв из исходного слова МАМА (n_М=2, n_А=2), таковы: MMAA, MAMA, MAAM, AMMA, AMAM, AAMM – 6 вариантов.

Пример 6. Перестановки из 0 и 1 при n₀=2, n₁=3 имеют вид: 00111, 01011, 01101, 01110, 10011, 10101, 10110, 11001, 11010, 11100 – всего 10 вариантов.

5. Сочетания. Это наборы, содержащие к различных элементов n-элементного множества без учёта порядка их расположения, иначе, сочетания — это к-элементные подмножества n-элементного множества.

Из каждого сочетания можно построить k! размещений перестановкой k элементов, поэтому

= =. (7)

Пример 7. Трёхэлементные подмножества для пятиэлементного множества {1, 2, 3, 4, 5} таковы: {1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 3, 4}, {1, 3, 5}, {1, 4, 5}, {2, 3, 4}, {2, 3, 5}, {2,4,5}, {3,4,5} — всего 10 вариантов.

6. Сочетания с повторениями. Это наборы, содержащие k элементов n-элементного множества без учёта порядка их расположения и с разрешением повторения. Каждое сочетание с повторением полностью определяется, если указано, сколько элементов x_i (1in) в него входит. Поставим в соответствие набору последовательность нулей и единиц по следующему правилу: последовательно для каждого элемента запишем столько единиц, сколько элементов x_i входит в сочетание, между отдельными группами единиц вставляется один нуль.

Таким образом, в последовательности будет k единиц и n-1 нулей. Различные перестановки n₁=k единиц и n₀=n-1 нулей определяют различные сочетания с повторениями

=P_k+n-1== (8)

Пример 7. Четырёхбуквенные сочетания с повторениями, построенные на множестве {А, М}, есть АААА, АААМ, ААММ, АМММ, ММММ.

Более подробное рассмотрение материала по комбинаторике можно найти, например в [5].

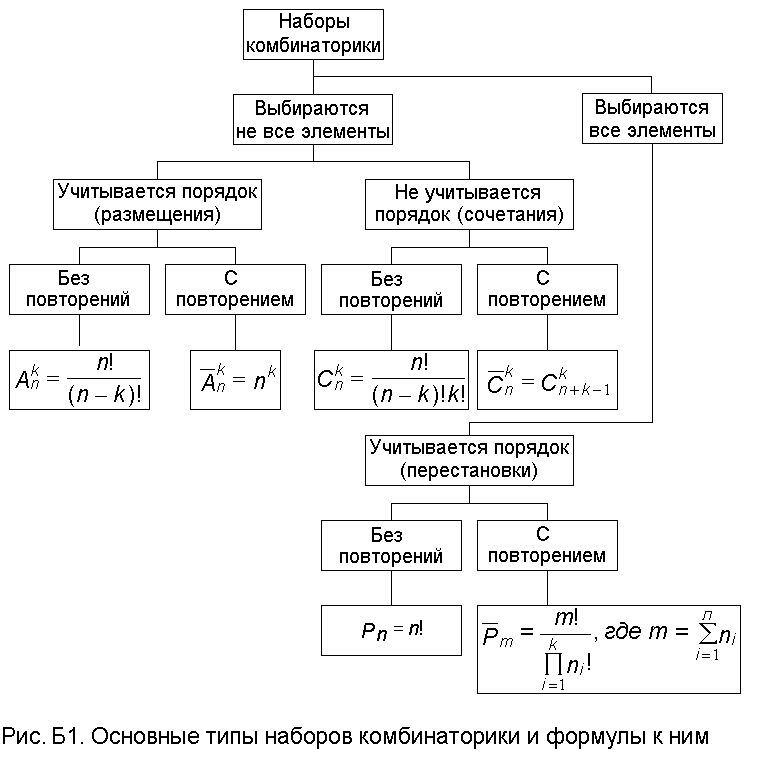
На рис. Б1 приведена классификация основных видов наборов и формул для определения количества наборов того или иного вида.

1 В некоторых источниках, например [5], используется термин выборка.

183