1.8 Оцінка складності алгоритму

Наближене рішення задачі про покриття засноване на такому міркуванні: Навіть скорочений перебір призводить до дуже трудомісткого процесу рішення, тому для отримання відповіді доводиться відмовлятися від гарантій побудови оптимального рішення (мінімального або найкоротшого); однак при цьому доцільно отримати не найгірший результат - хоча б безнадлишкове покриття , яке задовольняє необхідній умові. Тоді, на шкоду якості, можна значно спростити процес рішення.

Алгоритм побудови покриття, близького до найкоротшому, заснован на методі «мінімальний стовпець - максимальний рядок».

2. Алгоритм пірамідального сортування 2.1 Постановка задачі Сортування - один з найбільш поширених процесів сучасної обробки даних. Сортуванням називається розподіл елементів множини по групах відповідно до певних правил. Мета сортування - полегшити пошук елементів у відсортованому множині. У цьому сенсі елементи сортування присутні майже у всіх завданнях . Якщо мова йде про завдання сортування , звичайно передбачається , що вхідні дані складаються тільки з чисел. Перетворення алгоритму , призначеного для сортування чисел , в програму для сортування записів не представляє труднощів , хоча в практичній ситуації іноді виникають різні тонкі нюанси , які ускладнюють задачу програміста. Основними вимогами до ефективності алгоритмів сортування є , перш за все , ефективність за часом та економне використання пам'яті. Згідно з цими вимогами , прості алгоритми сортування (такі , як сортування вибором і сортування включенням ) не є дуже ефективними. Одним з ефективних алгоритмів вважається алгоритм пірамідального сортування , що працює в найгіршому , в середньому і в найкращому випадку (тобто гарантовано ) за Θ ( n log n ) операцій при сортуванні n елементів. Двійкове дерево - структура даних , у якій кожен елемент має левого та / або правого нащадка , або взагалі не має нащадків. В останньому випадку елемент називається листовим. Якщо елемент A має нащадка B , то елемент A називається батьком елемента B. У двійковому дереві існує єдиний елемент , який не має батьків; такий елемент називається кореневим. Піраміда - двійкове дерево , в якому значення кожного елемента більше або дорівнює значень дочірніх елементiв. Заповнів дерево елементами в про- довільній послідовності , можна легко його впорядкувати (легше , ніж вихідний список елементів) , перетворивши на піраміду. Найбiльший елемент піраміди знаходиться в її вершині. Суть алгоритму полягає в тому , що піраміда без додаткових витрат зберігається прямо в початковому масиві. У міру того , як розмір піраміди зменшується , вона займає все меншу частину масиву , а результат сортування записує -ся починаючи з кінця масиву на звільнені від піраміди місця. Відсортованою називається множина елементів розташованих у відповідності з певними заданими правилами.

2. Словесний опис алгоритму 1. Створимо сортувальне дерево з елементів масиву: A[i] ≥ A[2i+1] A[i] ≥ A[2i+2]

При 0<i<n/2

Виконання цієї дії потребує О(n) операцій. 2. Видалятимемо елементи з кореня по одному за крок та перебудовувати дерево. Таким чином на першому кроці міняємо місцями елементи А[1] і A[n], перетворюємо масив А[n-1] в сортувальне дерево. Далі міняємо місцями елементи А[1] і А[n-1], перетворюємо масив А[n-2] в сортувальне дерево. Цю послідовність дій повторюємо до тих пір, поки в сортувальному дерево не залишиться один елемент. Після закінчення сортування отримаємо А[n] – відсортований масив. Виконання цієї дії потребує O(n * log n) операцiй.

2. Вибір структур даних 1. Змінна n – кількість елементів масиву. 2. Масив A[n] – масив с вхідними даними, що повинно відсортувати. 3. Змінна buf – зберігає значення елементу для обміну місцями. 4. Змінна root –індекс поточного кореневого елементу. 5. Змінні left, right - індекси лівого і правого нащадкiв поточного кореня. 6. Змінна start – iндекс кореня, з якого починається вiдновлення пiрамiди. 7. Змінна fin – кількість елементів поточної піраміди 8. Змінні i, j – лічильники циклів.

3. Опис алгоритму

Блок 1. Ввод n та масиву A[n]. Блок 2. Знаходження максимального індексу елементу, який є батьком, по формулі i=(n/2)-1. Блок 3. Запуск циклу по змінній і з кроком -1, починаючи с (n/2)-1 до -1. Блок 4. Запуск процедури «Sort» з параметрами (i, n) , яка сортує «трійку» з коренем i. Блок 5. Завершення циклу по i. Блок 6. Запуск циклу по змінній i з кроком дорівнюючим -1, починаючи з N-1 до 0. Блок 7. Обмiн місцями значень кореневого та останнього елементiв пiрамiди. Блок 8. Знаходження максимального iндексу елемента, який є батьком в даному деревi. Блок 9. Запуск циклу по j з крком -1, починаючи з (i/2)-1 до -1. Блок 10. Процедура «Sort» з параметрами (j, i) , яка сортує «трiйку» c коренем j. Блок 11. Завершення циклу по j. Блок 12. Завершення циклу по i. Блок 13. Вивод вiдсортованого масив А[n].

2. Опис процедур Процедура «Sort». Блок 1. Розрахуємо iндекси кореня та його нащадкiв. Блок 2. Перевіряємо, чи iндекс правого нащадка менший за кількість елементів поточної піраміди. Якщо так, то переходимо до блоку 4, якщо ні – до блоку 3. Блок 3. Перевіряємо, чи iндекс лiвого нащадка менший за кількість елементів поточної піраміди. Якщо так, то переходимо до блоку 5, якщо ні – повертаємо масив. Блок 4. Перевіряємо, чи кореневий елемент менший за його лiвого нащадка. Якщо так, то переходимо до блоку 8, якщо ні – до блоку 6. Блок 5. Перевіряємо, чи значення лiвого нащадка бiльше за значення кореневого елементу. Якщо так, то переходимо до блоку 7, якщо ні – повертаеємо масив. Блок 6. Перевіряємо, чи кореневий елемент менший за свого правого нащадка. Якщо так, то переходимо до блоку 8, якщо ні – повертаеємо масив. Блок 7. Виконуємо процедуру «Swap» з параметрами (A[root], A[left]), яка мiняє мiсцями кореневий елемент з його лiвим нащадком. Блок 8. Перевіряємо, чи значення лiвого нащадка менше за значення правого нащадка. Якщо так, то переходимо до блоку 10, якщо ні – до блоку 9. Блок 9. Перевіряємо, чи значення правого нащадка менше за значення лiвого нащадка. Якщо так, то переходимо до блоку 11, якщо ні – повертаємо масив. Блок 10. Процедура «Swap» з параметрами (А[root], A[right]), яка мiняє мiсцями кореневий елемент з його правим нащадком. Блок 11. Процедура «Swap» з параметрами (A[root], A[left]), яка мiняє мiсцями кореневий елемент з його лiвим нащадком. Процедура «Swap» Блок 1. Елементи а1 та а2 міняються місцями.

3. Схема алгоритму

Малюнок 2.1 Схема алгоритму пірамідального сортування

Малюнок 2.2 Процедура «Sort».

Малюнок 2.3 Процедура «swap».

2.7 Контрольний приклад Крок 1. Введемо массив. n=8; A = {3, 21, 13, 15, 9, 27, 31, 4} 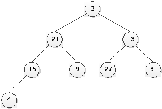Крок 2. i:=[n/2]-1; i=3. Крок 3. 1) i=3, fin=8, start=3. root:=3; left:=7; right:=8; Перевіряємо, чи right<fin? 8<8? Нi. Якщо нi: Перевіряємо left<fin? 7<8? Так. Якщо так: Перевіряємо A[left]>A[root]? 4>15. Ні. Якщо ні: Не змінюємо масив. 2) i=2, fin=8, start=2. root:=2; left:=5; right:=6; Перевіряємо, чи right<fin? 6<8? Так. Якщо так: Перевіряємо A[root]<A[left]? 13<27. Так. Якщо так: Перевіряємо A[left]<A[right]? 27<31. Так. Якщо так: buf:=A[root]; buf:=13; A[root]:=A[right]; A[2]:=31; А[right]:=buf; A[6]:=27; А = { 3, 21, 31, 15, 9, 27, 13, 4}

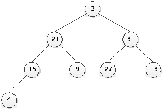3) i=1, fin=8, start=1. root:=1; left:=3; right:=4; Перевіряємо, чи right<fin? 4<8? Так. Якщо так: Перевіряємо A[root]<A [left]? 21<15. Ні. Якщо ні: Перевіряємо А[root]<A[right]? 21<9. Hі.

Якщо ні:

Не змінюємо масив. 4) i=0, fin=8, start=0. root:=0; left:=1; right:=2; Перевіряємо, чи right<fin? 2<8? Так. Якщо так: Перевіряємо A[root]<A[left]? 3<21. Так. Якщо так: Перевіряємо A[left]<A[right]? 21<31. Так. Якщо так: buf:=A[root]; buf:=3; A[root]:=A[right]; A[0]:=31; A[right]:=buf; A[2]:=3; A = { 31, 21, 3, 15, 9, 27, 13, 4}

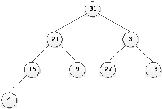
Крок 4. 1) i=7; buf:=A[0]; buf:=31; A[0]:=A[i]; A[0]:=4; A[i]:=buf; A[7]:=31; A = { 4, 21, 3, 15, 9, 27, 13, 31} 1.1) j=2, fin=7, start=2. root:=2; left:=5; right:=6;Перевіряємо, чи right<fin? 6<7? Так. Якщо так: Перевіряємо A[root]<A[left]? 3<27. Так. Якщо так: Перевіряємо A[left]<A[right]? 27<13. Нi. Якщо нi: buf:=A[root]; buf:=3; A[root]:=A[left]; A[2]:=27; A[left]:=buf; A[5]:=3; A = { 4, 21, 27, 15, 9, 3, 13, 31} 1.2)j=1, fin=7, start=1. root:=1; left:=3; right:=4; Перевіряємо, чи right<end? 4<7? Так. Якщо так: Перевіряємо A[root]<A[left]? 21<15. Ні. Якщо ні: Перевіряємо A[root]<A[right]? 21<9. Ні. Якщо ні: Не змінюємо масив.

1.3) j=0, fin=7, start=0. root:=0; left:=1; right:=2; Перевіряємо, чи right<fin? 2<7? Так. Якщо так: Перевіряємо A[root]<A[left]? 4<21. Так. Якщо так: Перевіряємо A[left]<A[right]? 21<27. Так. Якщо так: buf:=A[root]; buf:=4; A[root]:=A[right]; A[0]:=27; A[right]:=buf; A[2]:=4; A = { 27, 21, 4, 15, 9, 3, 13, 31}

2) i=6; buf:=A[0]; buf:=27; A[0]:=A[i]; A[0]:=13; A[i]:=buf; A[6]:=27; A = { 13, 21, 4, 15, 9, 3, 27, 31} 2.1) j=2, fin=6, start=2. root:=2; left:=5; right:=6; Перевіряємо, чи right<fin? 6<6? Нi. Якщо нi: Перевіряємо, чи left<fin? 5<6? Так. Якщо так: Перевіряємо A[root]<A[left]? 4<3. Нi. Якщо нi: Не змiнюємо масив.

2.2) j=1, fin=6, start=1. root:=1; left:=3; right:=4; Перевіряємо, чи right<fin? 4<6? Так. Якщо так: Перевіряємо A[root]<A[left]? 21<15. Нi. Якщо нi: Перевіряємо A[root]<A[right]? 21<9. Ні. Якщо ні: Не змінюємо масив. 2.3) j=0, fin=6, start=0. root:=0; left:=1; right:=2; Перевіряємо, чи right<fin? 2<6? Так. Якщо так: Перевіряємо A[root]<A[left]? 13<21. Так. Якщо так: Перевіряємо A[left]<A[right]? 21<4. Ні. Якщо ні: buf:=A[root]; buf:=13; A[root]:=A[left]; A[0]:=21; A[left]:=buf; A[1]:=13; A = { 21, 13, 4, 15, 9, 3, 27, 31} 3) i=5; buf:=A[0]; buf:=21; A[0]:=A[i]; A[0]:=3; A[i]:=buf; A[5]:=21; A = { 3, 13, 4, 15, 9, 21, 27, 31}

3.1) j=1, fin=5, start=1. root:=1; left:=3; right:=4; Перевіряємо, чи right<fin? 4<5? Так. Якщо так: Перевіряємо A[root]<A[left]? 13<15. Так. Якщо так: Перевіряємо A[left]<A[right]? 15<9. Нi. Якщо нi:

Перевіряємо A[right]<A[left]? 9<15. Так. Якщо так:

buf:=A[root]; buf:=13; A[root]:=A[left]; A[1]:=15; A[left]:=buf; A[3]:=13;

A = { 3, 15, 4, 13, 9, 21, 27, 31} 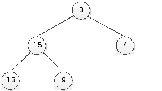3.2) j=0, fin=5, start=0. root:=0; left:=1; right:=2; Перевіряємо, чи right<fin? 2<5? Так. Якщо так: Перевіряємо A[root]<A[left]? 3<15. Так. Якщо так: Перевіряємо A[left]<A[right]? 15<4. Нi. Якщо нi:

Перевіряємо A[right]<A[left]? 4<15. Так. buf:=A[root]; buf:=3; A[root]:=A[left]; A[0]:=15; A[left]:=buf; A[1]:=3;

A = { 15, 3, 4, 13, 9, 21, 27, 31}

4) i=4; buf:=A[0]; buf:=15; A[0]:=A[i]; A[0]:=9; A[i]:=buf; A[4]:=15; A = { 9, 3, 4, 13, 15, 21, 27, 31} 4.1) j=1, fin=4, start=1. root:=1; left:=3; right:=4; Перевіряємо, чи right<fin? 4<4? Нi. Якщо нi: Перевіряємо, чи left<fin? 3<4? Так. Якщо так: Перевіряємо A[left]>A[root]? 13>3. Так. Якщо так: buf:=A[root]; buf:=3; A[root]:=A[left]; A[1]:=13; A[left]:=buf; A[3]:=3;

A = { 9, 13, 4, 3, 15, 21, 27, 31} 4.2)j=0, fin=4, start=0. root:=0; left:=1; right:=2; Перевіряємо, чи right<end? 2<4? Так. Якщо так: Перевіряємо A[root]<A[left]? 9<13. Так. Якщо так: Перевіряємо A[left]<A[right]? 13<4. Нi. Якщо нi: Перевіряємо A[right]<A[left]? 4<13. Так. Якщо так: buf:=A[root]; buf:=9; A[root]:=A[left]; A[0]:=13; A[left]:=buf; A[1]:=9; A = { 13, 9, 4, 3, 15, 21, 27, 31} 4) i=3; buf:=A[0]; buf:=13; A[0]:=A[i]; A[0]:=3; A[i]:=buf; A[3]:=13; A = { 3, 9, 4, 13, 15, 21, 27, 31} 4.1) j=0, fin=3, start=0. root:=0; left:=1; right:=2; Перевіряємо, чи right<end? 2<3? Так. Якщо так: Перевіряємо A[root]<A[left]? 3<9. Так. Якщо так: Перевіряємо A[left]<A[right]? 9<4. Нi.

Якщо ні:

Перевіряємо A[right]<A[left]? 4<9. Так.

Якщо так:

buf:=A[root]; buf:=3; A[root]:=A[left]; A[0]:=9; A[left]:=buf; A[1]:=3; A = { 9, 3, 4, 13, 15, 21, 27, 31}

5) i=2; buf:=A[0]; buf:=9; A[0]:=A[i]; A[0]:=4; A[i]:=buf; A[2]:=9; A = { 4, 3, 9, 13, 15, 21, 27, 31} 5.1) j=0, fin=2, start=0. root:=0; left:=1; right:=2; Перевіряємо, чи right<fin? 2<2? Нi. Якщо нi: Перевіряємо, чи left<fin? 1<2? Так. Якщо так: Перевіряємо A[left]>A[root]? 3>4. Нi. Якщо нi: Не змiнюємо масив. 6) i=1; buf:=A[0]; buf:=4; A[0]:=A[i]; A[0]:=3; A[i]:=buf; A[1]:=4; A = { 3, 4, 9, 13, 15, 21, 27, 31} Крок 5. Виведення результату: A = { 3, 4, 9, 13, 15, 21, 27, 31}

2.8 Оцінка ефективності алгоритму Пірамідальне сортування вважається одним з найбільш швидких алгоритмів сортування, так як на кожному кроці потрібно максимум log(2n) обмінів, необхідних для відновлення структури піраміди. Так як необхідно відсортувати n елементів , оцінка складності алгоритму - О(n*log(n)). Однак, через досить велику константу, даний алгоритм має сенс застосовувати лише на великих обсягах даних - починаючи від 500-1000 елементів, тільки тоді видно його виграш в ефективності. Для менших обсягів даних він малопридатний і краще використовувати інші алгоритми сортування, наприклад, сортування Шелла.